
《数学分析》教案 第十章定积分的应用 海南大学数学系 第十章定积分的应用 在上一章引入定积分概念时,曾把曲边梯形的面积、变速直线运动的路程表 示为积分和的极限,即要用定积分来加以度量。事实上,在科学技术中采用“分 割、作和、取极限”的方法去度量实际量得到了广泛的应用。本章意在建立度量 实际量的积分表达式的一种常用方法一一微元法,然后用微元法去阐述定积分在 某些几何、物理问题中的应用。 §1平面图形的面积 教学目标:掌握平面图形面积的计算公式。 教学内容:平面图形面积的计算公式. ()基本要求:掌握平面图形面积的计算公式,包括参量方程及极坐标方程 所定义的平面图形面积的计算公式. (②)较高要求:提出微元法的要领。 教学建议: (1)本节的重点是平面图形面积的计算公式,要求学生必须熟记并在应用中 熟练掌握。 (2)领会微元法的要领. 教学过程 1、微元法 众所周知,定积分 是由积分区间a,及被积函数f)所决定 的,而定积分对积分区间具有可加性,即如果把积分区间作为任意划分 A:=a<<x3<.<x<xn=b 记aM=fxd k=12,.,n
《数学分析》教案 第十章 定积分的应用 海南大学数学系 1 第十章 定积分的应用 在上一章引入定积分概念时,曾把曲边梯形的面积、变速直线运动的路程表 示为积分和的极限,即要用定积分来加以度量。事实上,在科学技术中采用“分 割、作和、取极限”的方法去度量实际量得到了广泛的应用。本章意在建立度量 实际量的积分表达式的一种常用方法——微元法,然后用微元法去阐述定积分在 某些几何、物理问题中的应用。 §1 平面图形的面积 教学目标:掌握平面图形面积的计算公式. 教学内容:平面图形面积的计算公式. (1) 基本要求:掌握平面图形面积的计算公式,包括参量方程及极坐标方程 所定义的平面图形面积的计算公式. (2) 较高要求:提出微元法的要领. 教学建议: (1) 本节的重点是平面图形面积的计算公式,要求学生必须熟记并在应用中 熟练掌握. (2) 领会微元法的要领. 教学过程: 1、微元法 众所周知,定积分 ( ) b a I f x dx = 是由积分区间 a b, 及被积函数 f x( ) 所决定 的,而定积分对积分区间具有可加性,即如果把积分区间作为任意划分 0 1 2 1 : n n x a x x x x b = = − 记 1 ( ) k k x k x I f x dx − = k n =1, 2,

《数学分析》教案 第十章定积分的应用 海南大学数学系 把积分值看作是分布在a上的总量,△山看作是在[]上的局部量,由积 分性质 1-2M 可见总量等于各个子区间上对应的局部量之和。因此,凡是用定积分描述的量都 应具有这种基本特征一一对积分区间的可加性。 另一方面,若f)eC.月,则积分上限函数国)=广四关于积分上限 x的导数'()=(x),于是用定积分度量的量 I(d()Ax 在[a,)上的任意标准子区同飞x+A上所对应的局部量△N的近似值()△r就 是()在点x处的微分d山,即 M≈f(x)△r=d (10.1) 且N-d=W-/()Ar=0Ay),所以,用定积分度量的量1在上x+△上的局 部量1所需要的近似值应是(10.1)表示的△x的线性函数)Ar,并且与△M 之差为Ar的高阶无穷小,通常,把式(10.1)冲的局部量△1的近似值山=f()本 称为积分微元。此时总量 I=[di=["f(x)dx 这种建立总量的积分表达式的方法,通常称为微元法。 2、平面图形的面积 下面我们根据不同坐标系下的曲线方程来建立平面图形面积公式。 (1)直角坐标系下计算平面图形的面积,首先考虑介于两曲线 y=fx)(∈C[a,b
《数学分析》教案 第十章 定积分的应用 海南大学数学系 2 把积分值看作是分布在 a b, 上的总量, k I 看作是在 x x k k −1 , 上的局部量,由积 分性质 1 n k k I I = = 可见总量等于各个子区间上对应的局部量之和。因此,凡是用定积分描述的量都 应具有这种基本特征——对积分区间的可加性。 另一方面,若 f x C a b ( ) , ,则积分上限函数 ( ) ( ) x a I x f u du = 关于积分上限 x 的导数 I x f x ( ) ( ) = ,于是用定积分度量的量 ( ) ( ) 0 1 ( ) lim n b k k a d k I f x dx f x → = = = 在 a b, 上的任意标准子区间 x x x , + 上所对应的局部量 I 的近似值 f x x ( ) 就 是 I x( ) 在点 x 处的微分 dI ,即 = I f x x dI ( ) (10.1) 且 − = − = I dI I f x x x ( ) ( ) 。所以,用定积分度量的量 I 在 x x x , + 上的局 部量 I 所需要的近似值应是(10.1)表示的 x 的线性函数 f x x ( ) ,并且与 I 之差为 x 的高阶无穷小。通常,把式(10.1)中的局部量 I 的近似值 dI f x dx = ( ) 称为积分微元。此时总量 ( ) b b a a I dI f x dx = = 这种建立总量的积分表达式的方法,通常称为微元法。 2、平面图形的面积 下面我们根据不同坐标系下的曲线方程来建立平面图形面积公式。 ( 1 ) 直 角 坐 标 系 下 计 算 平 面 图 形 的 面 积 , 首 先 考 虑 介 于 两 曲 线 y f x C a b = ( ) , ( )

《数学分析》教案 第十章定积分的应用 海南大学数学系 y=g(x(∈Ca,b)及直线x=a,x=b所围成的平面图形(图6.1)的面积o。 由于面积c是非均匀连续分布在区间血,)上 且对区间具有可加性的量,所以面积σ可以用定积 分来计算。 根据微元法,取【血)上的标准子区间 A1B y-g0) [区,x+△,在其上小曲边梯形ABCD的高可近似看 Oa xx+Ax 图 成不变的,它的面积△o可以用高为AD,宽为△r的 小矩形的面积近似代替,即 △o≈f(x)-g(x△r=da 于是所求图形的面积 G=Ido=f(x)-g(x)dx (10.2) 特别,如果8()=0,由连续函数y=f()、x轴及二直线x=a与x=b所围 成的平面图形(图6.2)的面积 o=∫fx (10.3) 例1、求由抛物线y=r与y=x所围成的平面图形(图6.3)的面积o。 图6.2 图6.3 x=y 求得交点(0,0)与,),由公式(6.1)知此图形的面积 3
《数学分析》教案 第十章 定积分的应用 海南大学数学系 3 y g x C a b = ( ) , ( ) 及直线 x a = , x b = 所围成的平面图形(图 6.1)的面积 。 由于面积 是非均匀连续分布在区间 a b, 上 且对区间具有可加性的量,所以面积 可以用定积 分来计算。 根 据 微 元 法 , 取 a b, 上 的 标 准 子 区 间 x x x , + ,在其上小曲边梯形 ABCD 的高可近似看 成不变的,它的面积 可以用高为 AD ,宽为 x 的 小矩形的面积近似代替,即 − = f x g x x d ( ) ( ) 于是所求图形的面积 ( ) ( ) b b a a = = − d f x g x dx (10.2) 特别,如果 g x( ) = 0 ,由连续函数 y f x = ( ) 、x 轴及二直线 x a = 与 x b = 所围 成的平面图形(图 6.2)的面积 ( ) b a = f x dx (10.3) 例 1、求由抛物线 2 y x = 与 2 y x = 所围成的平面图形(图 6.3)的面积 。 【解】 解联立方程 2 2 y x x y = = 求得交点 (0,0) 与 (1,1) ,由公式(6.1)知此图形的面积

《数学分析》教案 第十章定积分的应用 海南大学数学系 g=-r妆=小-恤 后6月 例2、求由抛物线x=1-2少与直线y=x所围成的平面图形(图6.)的面 积。 解:解联立方程 x=1-2y1 y=x 求得交点1-)和宁。此时,取为积分变量比较方便,相应的积分区间为 σ=-2y2-=-y-2y= 〔-号 例3:求血+血=l所围图形的面积。 解,方程血+山包括两条双曲线-与广 x和两条直线y=ex与 图6
《数学分析》教案 第十章 定积分的应用 海南大学数学系 4 1 1 1 2 2 2 0 0 = − = − = x x dx x x dx 3 3 2 2 2 1 1 1 3 3 3 3 3 0 x x − = − = 例 2、求由抛物线 2 x y = −1 2 与直线 y x = 所围成的平面图形(图 6.4)的面 积。 解:解联立方程 2 x y 1 2 y x = − = 求得交点 (− − 1, 1) 和 1 1 ( , ) 2 2 。此时,取 y 为积分变量比较方便,相应的积分区间为 1 1, 2 − ,于是 1 1 2 2 2 2 1 1 1 2 1 2 y y dy y y dy − − = − − = − − = 2 3 1 2 8 2 2 3 9 1 y y y − − = − 例 3:求 ln ln 1 x y + = 所围图形的面积。 解:方程 ln ln 1 x y + = 包括两条双曲线 e y x = 与 1 y ex = 和两条直线 y ex = 与

《数学分析》教案 第十章定积分的应用 海南大学数学系 。它们所成的平面形如国65所示 解联立方程 y=ex 解得交点e,》、Le)、,e)、e,),故所求面积 o+妆 1(ex-s+e-e 例4、设xca,a>0,x+g≥lnx,求使 I=∫(e+g-lnxk 最小的k与9。 解:若使积分I最小,此时直线y=+q应与曲线y=血x相切,故 k=(Inx)= ,切点坐标为《',-血,故切线方程为 y=kx-1-Ink (g=-1-ln) 从而 I=[(kx+q-InxXdx=*(b2-a2)-(1+InkX(b-a)-(blnb-alna-b+a) 令 盟-0-62-0 2 2
《数学分析》教案 第十章 定积分的应用 海南大学数学系 5 x y e = 。它们所围成的平面图形如图 6.5 所示。 解联立方程 1 e y x y ex y ex x y e = = = = 解得交点 1 ( ,1) e − 、 1 (1, ) e − 、(1, ) e 、( ,1) e ,故所求面积 1 1 1 1 e e x e ex dx dx ex e x − = − + − = 1 1 1 1 1 ( ) ( ) e e e x ex dx dx e e ex x e − − − + − = − 例 4、设 x a b , ,a 0,kx q x + ln ,求使 ( ln ) b a I kx q x dx = + − 最小的 k 与 q 。 解 :若使积 分 I 最小,此 时直 线 y kx q = + 应与曲线 y x = ln 相切 ,故 1 k x (ln ) x = = ,切点坐标为 1 ( , ln ) k k − − ,故切线方程为 y kx k q k = − − = − − 1 ln ( 1 ln ) 从而 2 2 ( ln ) ( ) (1 ln )( ) ( ln ln ) 2 b a k I kx q x dx b a k b a b b a a b a = + − = − − + − − − − + 令 1 2 2 ( ) 0 2 dI b a b a dk k − = − − = 解得驻点 2 k a b = + ,此时 ln 1 2 a b q + = − , 2 2 2 0 d I b a dk k − = ,所以当 2 k a b = +

《数学分析》教案 第十章定积分的应用 海市大学数学系 9=Ina+b 1 2 ,1的值最小。 (2)极坐标系下计算平面图形的面积。设曲线的极坐标方程是”=(),求 它与射线日=a、0=B所围成的曲边扇形(图6.6)的面积。其中 r=)eC[a,月]。取极角9为积分变量,它的变化范围为区间[a,P],则曲边 扇形的面积o可看作是展布在a,B上的量。 根据微元法,取[a,川上的标准子区间B,8+△d,在其上的小曲边扇形OAB 的面积△o可用半径为(0、中心角为△0的圆扇形面积来近似代替,即 Ao*r产t0a0=dc 于是所求曲边扇形的面积为 a=da ()do (10.4) 特别如图6.7所示的平面区域的面积 -r8 图6.6 0)do (6.4) 周6.8
《数学分析》教案 第十章 定积分的应用 海南大学数学系 6 ln 1 2 a b q + = − , I 的值最小。 (2)极坐标系下计算平面图形的面积。设曲线的极坐标方程是 r r = ( ) ,求 它与射线 = 、 = 所围成的曲边扇形(图 6.6 )的面积 。其中 r r C = ( ) , 。取极角 为积分变量,它的变化范围为区间 , ,则曲边 扇形的面积 可看作是展布在 , 上的量。 根据微元法,取 , 上的标准子区间 , + ,在其上的小曲边扇形 OAB 的面积 可用半径为 r( ) 、中心角为 的圆扇形面积来近似代替,即 1 2 ( ) 2 = r d 于是所求曲边扇形的面积为 ( ) 1 2 2 d r d = = (10.4) 特别如图 6.7 所示的平面区域的面积 ( ) 2 2 0 1 2 r d = (6.4)

《数学分析》教案 第十章定积分的应用 海南大学数学系 同理,设图形是由极坐标方程=(0、r=5(O)5(0>1(8》确定的二曲线 与射线0=a、0=B(B>a四所围成(图6.8,其面积 o-[5(o)-r(o]a0 (10.5) 例5、求四叶玫瑰线r=4c0s20所围成的平面图形的面积0(图6.9)。 解:由图形的对称性,所求面积等于第一象限中阴影部分面积的8倍。在曲 线的这一段上,对应的0从0变到4,于是由公式(10.4),有 (d0020d0 4八0 例6、求笛卡尔叶形线r+少-3如y=0所围成的平面图形的面积。(图 6.10)。 解:因为这条曲线无法从所给方程中解出x或y,表成显函数的形式,所以 不能按照公式(10.3)来计算面积。这就从一个侧面说明了掌握在极坐标下计算 平面图形面积的必要性。 将曲线方程化为极坐标方程,令x=rcos0,y=rsin8,代入函数方程,经 整理得 r=3asin0cos cos8+sin3日 0s0=号 于是根据公式(10.4),有 -tro0-8品0-
《数学分析》教案 第十章 定积分的应用 海南大学数学系 7 同理,设图形是由极坐标方程 1 r r = ( ) 、 2 r r = ( ) 2 1 ( ( ) ( )) r r 确定的二曲线 与射线 = 、 = ( ) 所围成(图 6.8),其面积 ( ) ( ) 2 2 2 1 1 2 r r d = − (10.5) 例 5、求四叶玫瑰线 r = 4cos2 所围成的平面图形的面积 (图 6.9)。 解:由图形的对称性,所求面积等于第一象限中阴影部分面积的 8 倍。在曲 线的这一段上,对应的 从 0 变到 4 ,于是由公式(10.4),有 ( ) 4 4 2 2 2 0 0 1 8 4 4 cos 2 2 r d d = = = 3 3 4 0 1 sin 4 4 (1 cos 4 ) 4 8 4 2 2 4 0 d + = + = 例 6、求笛卡尔叶形线 3 3 x y axy + − = 3 0 所围成的平面图形的面积 (图 6.10)。 解:因为这条曲线无法从所给方程中解出 x 或 y ,表成显函数的形式,所以 不能按照公式(10.3)来计算面积。这就从一个侧面说明了掌握在极坐标下计算 平面图形面积的必要性。 将曲线方程化为极坐标方程,令 x r = cos , y r = sin ,代入函数方程,经 整理得 3 3 3 sin cos 0 cos sin 2 a r = + 于是根据公式(10.4),有 ( ) 2 2 2 2 2 2 3 3 2 0 0 1 1 9 sin cos 2 2 (cos sin ) a r d d = = = +
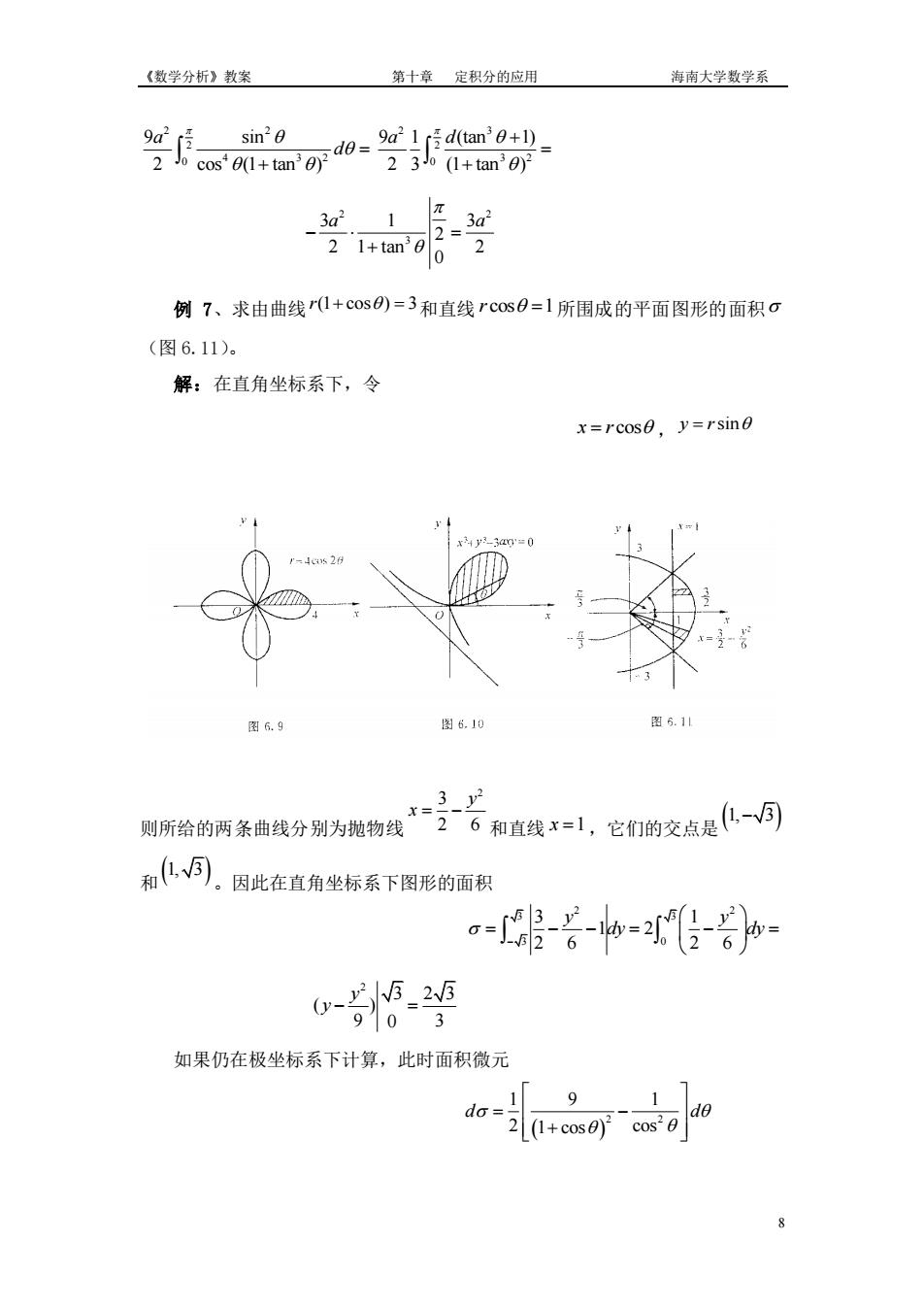
《数学分析》教案 第十章定积分的应用 海南大学数学系 cosan,m0n0-g/fdem'0+ sin20 23o1+tan'0 3a2 1 例7、求由曲线0+©os)=3和直线rcos0=1所围成的平面图形的面积o (图6.11) 解:在直角坐标系下,令 x=rcos0,y=rsine 图6.10 图6.11 则所给的两条曲线分别为抛物线 子产云有直线l,它的文点是-间 和人、同.因此在直角坐标系下图形的面积 0-5.25 9103 如果仍在极坐标系下计算,此时面积微元 do=9 17
《数学分析》教案 第十章 定积分的应用 海南大学数学系 8 2 2 2 3 2 2 4 3 2 3 2 0 0 9 sin 9 1 (tan 1) 2 cos (1 tan ) 2 3 (1 tan ) a a d d + = = + + 2 2 3 3 1 3 2 2 1 tan 2 0 a a − = + 例 7、求由曲线 r(1 cos ) 3 + = 和直线 r cos 1 = 所围成的平面图形的面积 (图 6.11)。 解:在直角坐标系下,令 x r = cos , y r = sin 则所给的两条曲线分别为抛物线 2 3 2 6 y x = − 和直线 x =1 ,它们的交点是 (1, 3 − ) 和 (1, 3) 。因此在直角坐标系下图形的面积 2 2 3 3 3 0 3 1 1 2 2 6 2 6 y y dy dy − = − − = − = 2 3 2 3 ( ) 9 3 0 y y − = 如果仍在极坐标系下计算,此时面积微元 ( ) 2 2 1 9 1 2 cos 1 cos d d = − +

《数学分析》教案 第十章定积分的应用 海南大学数学系 因为两鱼线交点为-骨和2 ,于是所求面积0可表作 9 11 G里o4 coso 这个积分计算起来就复杂多了。可见计算平面图形的面积一般要先画出草 图,选择在直角坐标系,还是在极坐标系下的方程来表达边界曲线,目的应该使 所得曲线方程简单易于积分运算。 (3)用参数方程表示的曲线所围成的平面图形面积的计算。如果所给曲线 方程为参数形式 ∫x=p) asisB ly=v(t) (10.6) 其中(0单调增加,且(回=a,()=b,p0,(0,(∈C[a,月,则 由曲线(6.6X、x轴及直线x=ax=b所围成的平面图形面积(图6.2) o=∫w()lo')d (10.7) 事实上,由条件知,存在反函数'=(),因而曲线方程为 y=w[p'(x)] a≤x≤b 所以由公式(10.2)知,该平面图形的面积为 。=y[o'(x小t=wo'0h (10.8) 上述公式当=p(0单调减少时仍成立,这时(0s0,同时a≥B。 例8、求旋轮线 [x=a(t-sint) a>0,0s1s2元 y=a(t-cost) 与x轴所围成图形的面积
《数学分析》教案 第十章 定积分的应用 海南大学数学系 9 因为两曲线交点为 (2, ) 3 − 和 (2, ) 3 ,于是所求面积 可表作 ( ) 3 3 2 2 3 3 1 9 1 2 cos 1 cos d d − − = = − = + ( ) 3 2 2 0 9 1 1 cos cos d − + 这个积分计算起来就复杂多了。可见计算平面图形的面积一般要先画出草 图,选择在直角坐标系,还是在极坐标系下的方程来表达边界曲线,目的应该使 所得曲线方程简单易于积分运算。 (3)用参数方程表示的曲线所围成的平面图形面积的计算。如果所给曲线 方程为参数形式 ( ) ( ) x t t y t = = (10.6) 其中 (t) 单调增加,且 ( ) = a, ( ) = b, (t) ; (t) , (t C ) , ,则 由曲线(6.6)、 x 轴及直线 x a x b = = , 所围成的平面图形面积(图 6.2) (t t dt ) ( ) = (10.7) 事实上,由条件知,存在反函数 ( ) 1 t x − = ,因而曲线方程为 ( ) 1 y x a x b − = 所以由公式(10.2)知,该平面图形的面积为 ( ) ( ) ( ) 1 b b a a x dx t t dt − = = (10.8) 上述公式当 x t = ( ) 单调减少时仍成立,这时 (t) 0 ,同时 。 例 8、求旋轮线 ( sin ) 0,0 2 ( cos ) x a t t a t y a t t = − = − 与 x 轴所围成图形的面积

《数学分析》教案了 第十章定积分的应用 海市大学数学系 解:由公式(10.8),有 -(()di=f"a(1-cosa(1-cosrydi- (-cosdi"sind"sin'du- 1w号=3ar
《数学分析》教案 第十章 定积分的应用 海南大学数学系 10 解:由公式(10.8),有 ( ) ( ) 2 2 0 0 t t dt a t a t dt (1 cos ) (1 cos ) = = − − = 2 2 2 2 2 2 4 2 4 0 0 0 (1 cos ) 4 sin 16 sin 2 t a t dt a dt a udu − = = = 2 2 3 1 16 3 4 2 2 a a =