
《数学分析》教案 第十一章反常积分 海南大学数学系 第十一章反常积分 教学要点: 反常积分收敛和发散的概念及敛散性判别法。 教学内容: §1反常积分的概念(4学时) 反常积分的引入,两类反常积分的定义反常积分的计算 §2无穷积分的性质与收敛判别(4学时) 无穷积分的性质,非负函数反常积分的比较判别法,Cauchy判别法,反 常积分的Dirichlet判别法与Abel判别法。 §3瑕积分的性质与收敛判别 瑕积分的性质,绝对收敛,条件收敛,比较法则。 教学要求: 掌握反常积分敛散性的定义,奇点,掌握一些重要的反常积分收敛和发散的 例子,理解并掌握绝对收敛和条件收敛的概念,并能用反常积分的Cauchy收敛 原理、非负函数反常积分的比较判别法、Cauchy判别法,以及一般函数反常积 分的Abel、Dirichlet判别法判别基本的反常积分。 1.反常积分的收敛性及其收敛性的判别法是本章的重点。 2.两类反常积分的性质及其收敛性判别法有很多相似之处,应引导学生加以 类比。 §1反常积分概念 教学目标:掌握反常积分的定义与计算方法. 教学内容:无穷积分:瑕积分。 教学建议: 讲清反常积分是变限积分的极限 教学过程:
《数学分析》教案 第十一章 反常积分 海南大学数学系 1 第十一章 反常积分 教学要点: 反常积分收敛和发散的概念及敛散性判别法。 教学内容: §1 反常积分的概念 (4 学时) 反常积分的引入,两类反常积分的定义 反常积分的计算。 §2 无穷积分的性质与收敛判别 (4 学时) 无穷积分的性质,非负函数反常积分的比较判别法,Cauchy 判别法,反 常积分的 Dirichlet 判别法与 Abel 判别法。 §3 瑕积分的性质与收敛判别 瑕积分的性质,绝对收敛,条件收敛,比较法则。 教学要求: 掌握反常积分敛散性的定义,奇点,掌握一些重要的反常积分收敛和发散的 例子,理解并掌握绝对收敛和条件收敛的概念,并能用反常积分的 Cauchy 收敛 原理、非负函数反常积分的比较判别法、Cauchy 判别法,以及一般函数反常积 分的 Abel、Dirichlet 判别法判别基本的反常积分。 1.反常积分的收敛性及其收敛性的判别法是本章的重点. 2.两类反常积分的性质及其收敛性判别法有很多相似之处,应引导学生加以 类比。 §1 反常积分概念 教学目标:掌握反常积分的定义与计算方法. 教学内容:无穷积分;瑕积分. 教学建议: 讲清反常积分是变限积分的极限. 教学过程:

《数学分析》教案 第十一章反常积分 海南大学数学系 一、问题的提出 l、为什么要推广Riemann积分 定积分∫心fx)k有两个明显的缺陷:其一,积分区间[a,b]必须是有限区间: 其二,若fea,b],则3M>0,使得对于任意的x∈[a,b],If(x)sM(即有 界是可积的必要条件)。这两个缺陷限制了定积分的应用,因为在许多实际问题 和理论问题中涉及到积分区间是无穷区间或被积函数出现无界的情形。 例1(第二字宙速度问题)、在地球表面初值发射火箭,要是火箭克服地球 引力,无限远离地球,问初速度至少多大? 解:设地球半径为R,,火箭质量为m,地面重力加速度为8,有万有引 力定理,在距地心x处火箭受到的引理为 F 于是火箭上升到距地心”处需要做到功为 当”→0时,其极限就是火箭无限远离地球需要作的功 =”=e 在由能量守恒定律,可求得处速度%至少应使 mi-mgR2gR11.2(n/s) 例2、从盛满水开始打开小孔,问需多长时间才 能把桶里水全部放完? 解:由物理学知识知道,(在不计摩擦情况下), 桶里水位高度为-x时,水从小孔里流出的速度为 =2g(h-x) 设在很短一段时间△“内,桶里水面降低的高度为△x,则有下面关系:
《数学分析》教案 第十一章 反常积分 海南大学数学系 2 一、 问题的提出 1、为什么要推广 Riemann 积分 定积分 ( ) b a f x dx 有两个明显的缺陷:其一,积分区间[a,b]必须是有限区间; 其二,若 f R a b [ , ] ,则 M 0 ,使得对于任意的 x a b [ , ],| ( ) | f x M (即有 界是可积的必要条件)。这两个缺陷限制了定积分的应用,因为在许多实际问题 和理论问题中涉及到积分区间是无穷区间或被积函数出现无界的情形。 例 1(第二宇宙速度问题)、在地球表面初值发射火箭,要是 火箭克服地球 引力,无限远离地球,问初速度至少多大? 解: 设地球半径为 ,火箭质量为 ,地面重力加速度为 ,有万有引 力定理,在距地心 处火箭受到的引理为 于是火箭上升到距地心 处需要做到功为 当 时,其极限就是火箭无限远离地球需要作的功 在由能量守恒定律,可求得处速度 至少应使 例 2、 从盛满水开始打开小孔,问需多长时间才 能把桶里水全部放完? 解: 由物理学知识知道,(在不计摩擦情况下), 桶里水位高度为 时,水从小孔里流出的速度为 设在很短一段时间 内,桶里水面降低的高度为 ,则有下面关系:
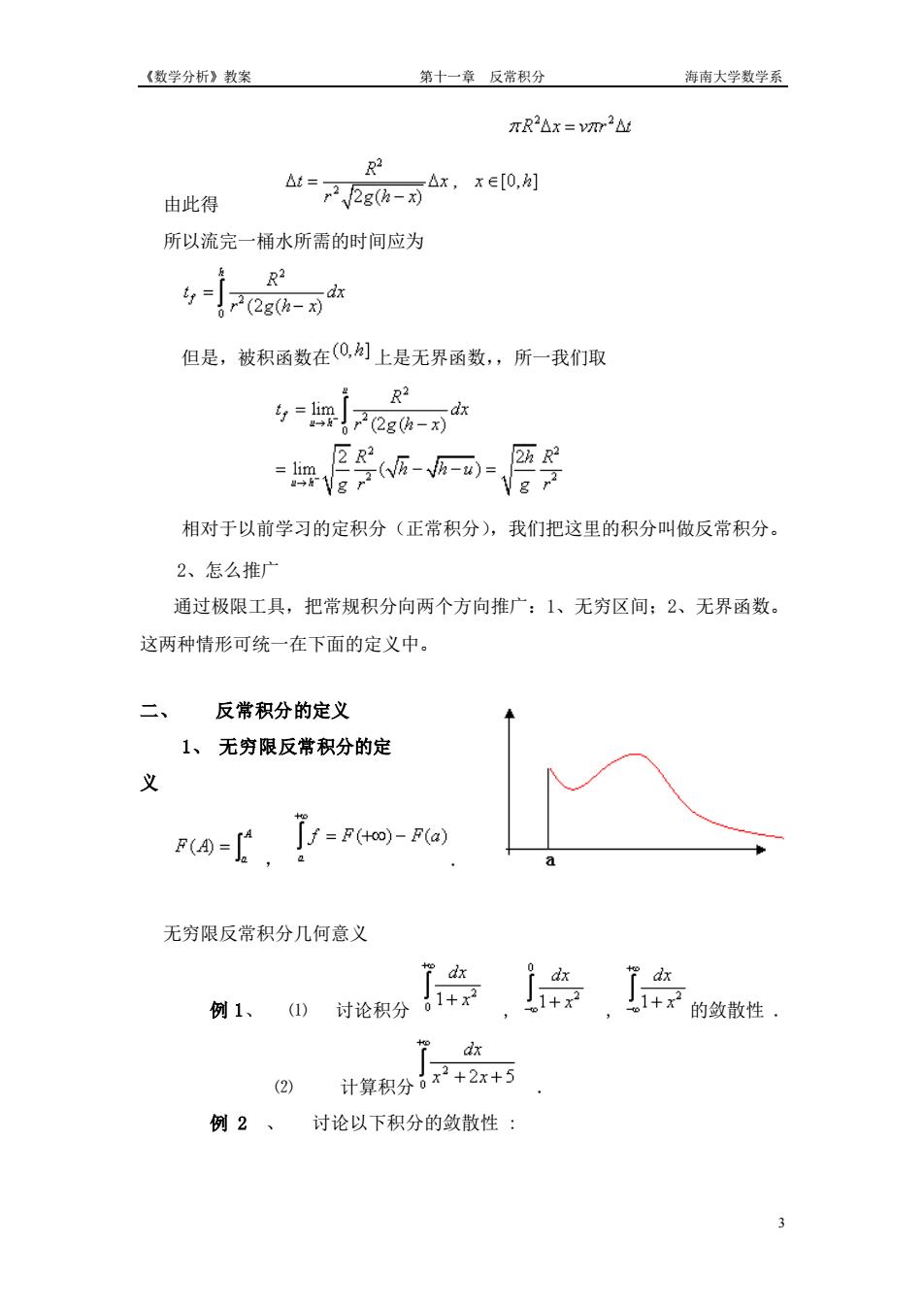
《数学分析》教案 第十一章反常积分 海南大学数学系 πR2Ax=m2 由此得 如-7可2h-可,e 所以流完一桶水所需的时间应为 -水 但是,被积函数在0,月上是无界函数,所一我们取 4=ee8h-对 G VE 相对于以前学习的定积分(正常积分),我们把这里的积分叫做反常积分 2、怎么推广 通过极限工具,把常规积分向两个方向推广:1、无穷区间:2、无界函数 这两种情形可统一在下面的定义中。 二、反常积分的定义 1、无穷限反常积分的定 义 (0=, 「/=F(to)-F(a) 无穷限反常积分几何意义 例1、(1)讨论积分 票产.品的 dx (2) 计算积分。x+2x+5 例2、 讨论以下积分的敛散性: 3
《数学分析》教案 第十一章 反常积分 海南大学数学系 3 由此得 所以流完一桶水所需的时间应为 但是,被积函数在 上是无界函数,所一我们取 相对于以前学习的定积分(正常积分),我们把这里的积分叫做反常积分。 2、怎么推广 通过极限工具,把常规积分向两个方向推广:1、无穷区间;2、无界函数。 这两种情形可统一在下面的定义中。 二、 反常积分的定义 1、 无穷限反常积分的定 义 , . 无穷限反常积分几何意义 例 1、 ⑴ 讨论积分 , , 的敛散性 . ⑵ 计算积分 . 例 2 、 讨论以下积分的敛散性 :
《数学分析》教案 第十一章反常积分 海南大学数学系 (2) 号血列 的敛散性 2、瑕积分的定义:以点b为瑕点给出定义.然后就点为瑕点、点 cE (a,b) 为瑕点以及有多个瑕点的情况给出说明. dx 例4、 判断积分-云的敛散性。 例5、 讨论瑕积分(9>0 增dx 的微散性,并讨论积分 的敛散 性 瑕积分与无穷积分的关系:设函数()连续,b为瑕点。有 3-a ,把瑕积分化成 了无穷积分: 设a>0,有 把无穷积分化成了瑕 积分 作业:P-269:1,2
《数学分析》教案 第十一章 反常积分 海南大学数学系 4 ⑴ ; ⑵ . 例 3、讨论积分 的敛散性 . 2、 瑕积分的定义: 以点 为瑕点给出定义. 然后就点 为瑕点、点 为瑕点以及有多个瑕点的情况给出说明. 例 4、 判断积分 的敛散性 . 例 5、 讨论瑕积分 的敛散性 , 并讨论积分 的敛散 性 . 瑕积分与无穷积分的关系: 设函数 连续 , 为瑕点. 有 , 把瑕积分化成 了无穷积分; 设 , 有 ,把无穷积分化成了瑕 积分 作业: P-269: 1,2