
《数学分析》下册 第十七章多元函数的微分学 海南大学数学系 第十七章多元函数的微分学 §1可微性 教学目的掌握多元函数偏导数,可微性与全微分的定义,可微的必要条件 教学要求 (①)基本要求:掌握多元函数偏导数,可微性与全微分的定义,熟记可微的 必要条件与充分条件。 (②)较高要求:切平面存在定理的证明。 教学建议 ()本节的重点是多元函数偏导数,可微性与全微分的定义. (②)通过讨论可微的必要条件与充分条件,弄清多元函数连续,存在偏导数 与可微这三个分析性质之间的关系。 教学程序 一、可徽性与全徽分: 由一元函数可微性引入二元函数可微性. 定义1(可微性)设函数z=fx,)在点P(xo,%)的某邻域UB。)内有定 义,对于UP)中的点Px,)=(x。+△x,6+△,若函数f在点B处的全增量 可表示为△z=fx。+△x,6+△y)-fx,=A△x+BAy+(p列,其中A,B 是仅与点P有关的常数,p=√△x2+△,(p)是较p高阶的无穷小量,则称函 数f在点P处可微 全微分:|s=(%)=AAx+B弘y 当△x,△充分小时 dz≈Az fx,功≈fxo,o)+A(x-xo)+By-yo) 例1考查函数fx,)=y在点(x,)处的可微性 二、偏导数 (一)、偏导数的定义、记法
《数学分析》下册 第十七章 多元函数的微分学 海南大学数学系 1 第十七章 多元函数的微分学 §1 可微性 教学目的 掌握多元函数偏导数,可微性与全微分的定义,可微的必要条件. 教学要求 (1) 基本要求:掌握多元函数偏导数,可微性与全微分的定义,熟记可微的 必要条件与充分条件. (2) 较高要求:切平面存在定理的证明. 教学建议 (1)本节的重点是多元函数偏导数,可微性与全微分的定义. (2) 通过讨论可微的必要条件与充分条件,弄清多元函数连续,存在偏导数 与可微这三个分析性质之间的关系. 教学程序 一、 可微性与全微分: 由一元函数可微性引入二元函数可微性. 定义 1(可微性) 设函数 z f x y = ( , ) 在点 0 0 0 P x y ( , ) 的某邻域 0 U P( ) 内有定 义,对于 0 U P( ) 中的点 0 0 P x y x x y y ( , ) ( , ) = + + ,若函数 f 在点 P0 处的全增量 可表示为 0 0 = + + − = + + z f x x y y f x y A x B y ( , ) ( , ) ( ) ,其中 A,B 是仅与点 P0 有关的常数, 2 2 = + x y , ( ) 是较 高阶的无穷小量,则称函 数 f 在点 P0 处可微。 全微分: 当 x y , 充分小时 0 0 0 0 ( , ) ( , ) ( ) ( ) dz z f x y f x y A x x B y y + − + − . 例 1 考查函数 f (x, y) = xy 在点 ( , ) 0 0 x y 处的可微性 . 二 、 偏导数 (一)、偏导数的定义、记法
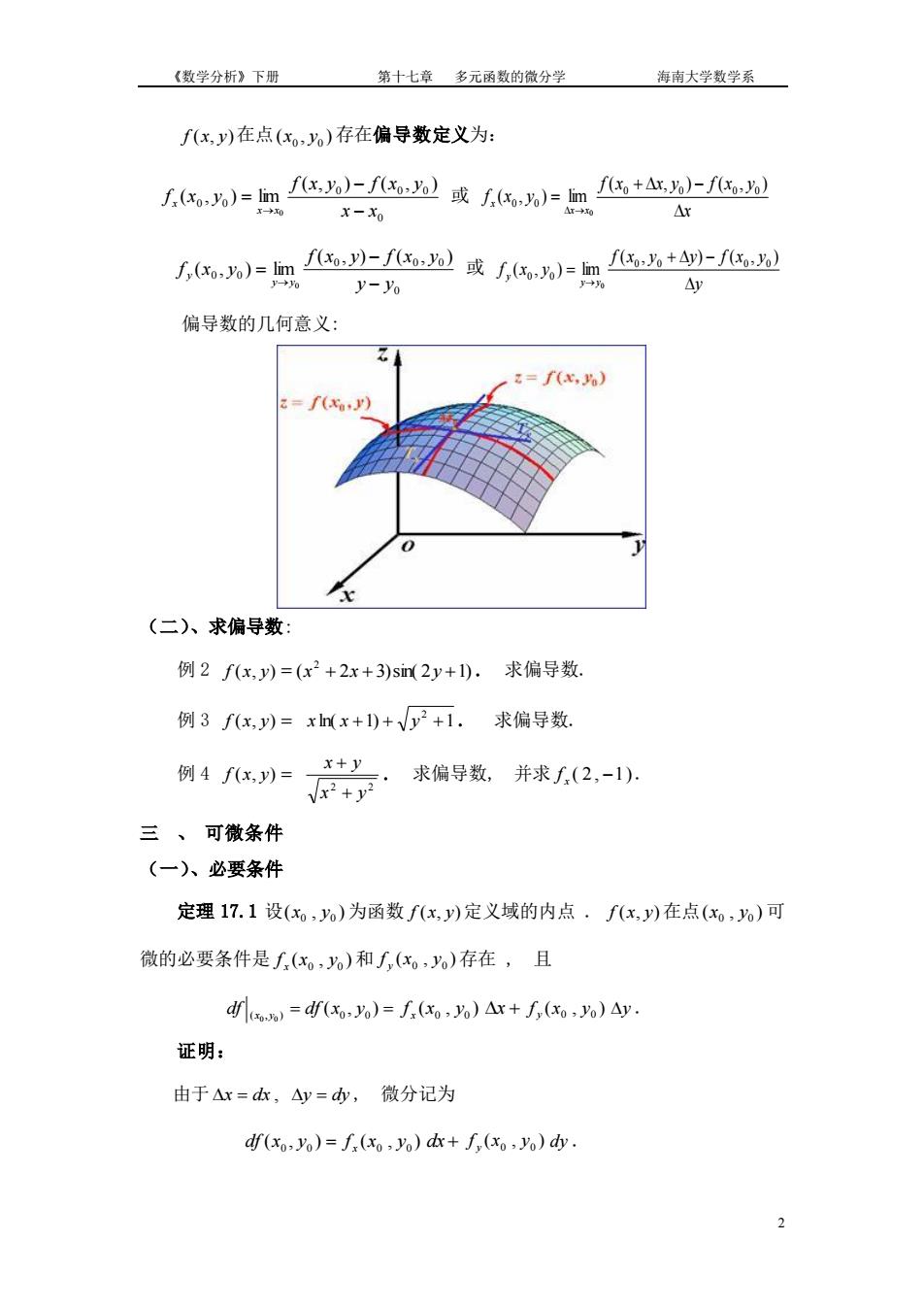
《数学分析》下册 第十七章多元函数的微分学 海南大学数学系 ∫x,)在点(x,)存在偏导数定义为: w=▣W园或么=飞+-园 x-X =》或化,=▣+- y-% Ay 偏导数的几何意义: 8=fx,) f( (二)、求偏导数 例2f(x,y)=(x2+2x+3)s(2y+1).求偏导数. 例3f(x,y)=xnx+1)+V少2+1.求偏导数. 例4(x,)= 产行·求导数。并求2,-1. x+y 三、可微条件 (一)、必要条件 定理17.1设(x0,%)为函数f(x,y)定义域的内点·f(x,y)在点(xo,%)可 微的必要条件是∫(x,%)和了,(x,)存在,且 d=dr(x%)=∫(xo,)△r+(,%)Ay. 证明: 由于△x=dk,Ay=,微分记为 df(xo.yo)=f(xo,vo)dx+f(xo,yo)dy. 2
《数学分析》下册 第十七章 多元函数的微分学 海南大学数学系 2 f (x, y) 在点 ( , ) 0 0 x y 存在偏导数定义为: 0 0 0 0 0 0 ( , ) ( , ) ( , ) lim 0 x x f x y f x y f x y x x x − − = → 或 x f x x y f x y f x y x x x + − = → ( , ) ( , ) ( , ) lim 0 0 0 0 0 0 0 0 0 0 0 0 0 ( , ) ( , ) ( , ) lim 0 y y f x y f x y f x y y y y − − = → 或 y f x y y f x y f x y y y y + − = → ( , ) ( , ) ( , ) lim 0 0 0 0 0 0 0 偏导数的几何意义: (二)、求偏导数: 例 2 f (x, y) = ( 2 3)sin( 2 1) 2 x + x + y + . 求偏导数. 例 3 f (x, y) = ln( 1) 1 2 x x + + y + . 求偏导数. 例 4 f (x, y) = 2 2 x y x y + + . 求偏导数, 并求 ( 2 , −1) x f . 三 、 可微条件 (一)、必要条件 定理 17.1 设 ( , ) 0 0 x y 为函数 f (x, y) 定义域的内点 . f (x, y) 在点 ( , ) 0 0 x y 可 微的必要条件是 ( , ) 0 0 f x y x 和 ( , ) 0 0 f x y y 存在 , 且 ( , ) = ( 0 , 0 ) = 0 0 df df x y x y ( , ) 0 0 f x y x x + ( , ) 0 0 f x y y y . 证明: 由于 x = dx , y = dy , 微分记为 df (x0 , y0 ) = ( , ) 0 0 f x y x dx + ( , ) 0 0 f x y y dy

《数学分析》下册 第十七章多元函数的微分学 海南大学数学系 定理17.1给出了计算可微函数全微分的方法.但是两个偏导数存在只是可 微的必要条件,而不是充分条件。 例5.考查函数 川=F+产+2≠0. xy 0, x2+y2=0 在原点的可微性 这个例子说明,偏导存在不一定可微,(这一点与一元函数不同!) (二)、充分条件 定理17.2(可微的充分条件)若函数:=fx,)的偏导数在的某邻域 内存在,且和了,在点(x。,y)处连续·则函数f在点(x,)可微。 定理17.3(中值定理)设函数∫在点(x。,)的某邻域内存在偏导数,若 (x,)属于该邻域,则存在5=x。+日,(x-x)和7=%+0,0-), 0<0<1,0<0<1,使得 f(x,y)-fx0,o)=f(5,yx-x)+f,(x,7y-%). (证路) 推论若f,(x,y)在点(x,)处连续,f(x,y)点(x。,)存在,则函数 ∫在点(x,)可微 证明:f(x。+△x,%+Ay)-f(o,%) =[fx,+△x,o+Ay)-f(x+△x,小+[fx,+△x,%)-f(x0,%】 =f(xo+Ar,o+y)Ay+(xo:Yo)Ax+aAr 0<0<1,a→0 =[f,(x,%)+B]△y+f(xo,%)△r+aAx B→0 =f(xo.o)Ax+f(xo,Yo)Ay+aAx+BAy 即f在点(x,%)可微 3
《数学分析》下册 第十七章 多元函数的微分学 海南大学数学系 3 定理 17.1 给出了计算可微函数全微分的方法. 但是两个偏导数存在只是可 微的必要条件, 而不是充分条件. 例 5.考查函数 + = + = + 0 , 0 , 0 , ( , ) 2 2 2 2 2 2 x y x y x y x y f x y 在原点的可微性 . 这个例子说明,偏导存在不一定可微,(这一点与一元函数不同!) (二)、充分条件 定理 17.2(可微的充分条件)若函数 z = f (x, y) 的偏导数在的某邻域 内存在 , 且 x f 和 y f 在点 ( , ) 0 0 x y 处连续 . 则函数 f 在点 ( , ) 0 0 x y 可微。 定理 17.3(中值定理)设函数 f 在点 ( , ) 0 0 x y 的某邻域内存在偏导数 . 若 (x, y) 属于该邻域 , 则存在 ( ) 0 1 0 = x + x − x 和 ( ) 0 2 0 = y + y − y , 0 1 1, 0 2 1, 使得 ( , ) ( , ) ( , )( ) ( , )( ) 0 0 0 0 0 f x y f x y f y x x f x y y − = x − + y − . ( 证略 ) 推论 若 f (x, y) y 在点 ( , ) 0 0 x y 处连续, f (x, y) x 点 ( , ) 0 0 x y 存在 , 则函数 f 在点 ( , ) 0 0 x y 可微 证明: f (x + x , y + y) − f 0 0 ( , ) 0 0 x y ( , ) ( , ) ( , ) ( , ) 0 0 0 0 0 0 0 0 = f x + x y + y − f x + x y + f x + x y − f x y 0 0 0 0 ( , ) ( , ) 0 1, 0 y x = + + + + → f x x y y y f x y x x 0 0 0 0 ( , ) ( , ) y x = + + + f x y y f x y x x → 0 f x y x f x y y x y = x ( 0 , 0 ) + y ( 0 , 0 ) + + . 即 f 在点 ( , ) 0 0 x y 可微

《数学分析》下册 第十七章多元函数的微分学 海南大学数学系 (x2+y)sin- x2+y2≠0, 例6fx,) x+y2 0, x2+y2=0. 验证函数fx,)在点(0,0)可微,但了和f,在点(0,0)处不连续 证明: ”+扩@→0,cm→0. 1 因此f(x,)=o(p),即f(x,)-f0.0)=0Ar+0△y+o(p), f在点(0,0)可微,∫(0,0)=0,∫,(0,0)=0.但(x)≠(0,0)时,有 1 1 f(x.y)=2xsin- +FF+FF+万 沿方向:只+,马+反不存在,→沿方向y红极限 巴F+可0不存在:又红)→(0.0)时, 1 1 2xsin- vx+y →0,因此,G)不存在,人在点(0,0)处不连续。 由∫关于x和y对称,∫,也在点(0,0)处不连续· (三)、连续、偏导数存在及可徽之间的关系: 这三个概念之间的关系可以用下图表示(在(x,)点)》 ∫连续 人,∫连续 f可微 了,了,存在 在上述关系中,反方向均不成立。下面以(x。,)=(0,0)点为例,逐一讨论。 例1x功=+r+少0 x2+y2=0
《数学分析》下册 第十七章 多元函数的微分学 海南大学数学系 4 例 6 + = + + + = 0 , 0 . , 0 , 1 ( )sin ( , ) 2 2 2 2 2 2 2 2 x y x y x y x y f x y 验证函数 f (x, y) 在点 ( 0 , 0 ) 可微 , 但 x f 和 y f 在点 ( 0 , 0 ) 处不连续 . 证明: 0 , ( , ) (0 , 0). 1 sin ( , ) 2 2 2 2 → → + = + x y x y x y f x y 因此 f (x, y) = () , 即 f (x, y) − f (0,0) = 0x + 0y +() , f 在点 (0 , 0) 可微 , f x (0,0) = 0 , f y (0,0) = 0 . 但 (x, y) ( 0 , 0 ) 时, 有 2 2 2 2 2 2 1 cos 1 ( , ) 2 sin x y x y x x y f x y x x + + − + = , 沿方向 y = kx, 0 2 2 0 2 | | 1 lim lim x k x x y x x x + = + → → 不存在, 沿方向 y = kx, 极限 0 2 2 2 2 1 lim cos x y x y x x + + → 不存在 ; 又 (x, y) → ( 0 , 0 ) 时, 0 1 2 sin 2 2 → x + y x ,因此, lim ( , ) ( , ) (0,0) f x y x x y → 不存在 , x f 在点 ( 0 , 0 ) 处不连续. 由 f 关于 x 和 y 对称, y f 也在点 ( 0 , 0 ) 处不连续 . (三)、连续、偏导数存在及可微之间的关系: 这三个概念之间的关系可以用下图表示(在 ( , ) 0 0 x y 点) 3 1 2 4 在上述关系中,反方向均不成立。下面以 ( , ) (0,0) x0 y0 = 点为例,逐一讨论。 例 1 + = + = + 0, 0 , 0 ( , ) 2 2 2 2 2 2 x y x y x y xy f x y x f , y f 连续 f 可微 f 连续 x f , y f 存在

《数学分析》下册 第十七章多元函数的微分学 海南大学数学系 这是教材中的典型例题,f,(0,0)-f,(0,0)=0均存在,但f(x,y)在(0.0)点不可 微,且mf心,)不存在,即f心x)在(0,0)点不连续 例2fx,)=√x2+y,这是上半圆锥,显然在(0.0)点连续, x9=0=f00. f(x.0)-1(00x>0 x=x=-1,x<0 故∫(0,0)不存在。由x,y的对称性,∫,0,0)不存在。从而,fx,)在(0,0) 点不可微(否则,∫0,0),f,(0,0)均存在)。 1 倒3功-+m24+r0 0, x2+y2=0 f00=0:/100=m, 由x,y的对称性,f,0,0)=0。 fx,y)-f0,0)-f(0.0)x-f,(0,0)y vx+y 立可08 1 vx2+y2 y→0 故fx,y)在(0,0)点可微。且df(0,0)=f(0,0)d+∫0,0)y=0 f,(x.y)= 2m4yy4+y0 0, x2+y2=0 取点列B)七2=0,显然P化)→00X→四 f(xn,yn)=-22 cos2n→-(n→o) 故m∫(x,y)不存在,从而∫(x)在(0,0)点不连续。由x,y的对称性,f,(x) 8 5
《数学分析》下册 第十七章 多元函数的微分学 海南大学数学系 5 这是教材中的典型例题, f x (0,0) = f y (0,0) = 0 均存在,但 f (x, y) 在 (0,0) 点不可 微,且 lim ( , ) 0 0 f x y y x → → 不存在,即 f (x, y) 在 (0,0) 点不连续。 例 2 2 2 f (x, y) = x + y ,这是上半圆锥,显然在 (0,0) 点连续, lim ( , ) 0 (0,0) 0 0 f x y f y x = = → → , 但 − = = = − 1, 0 ( ,0) (0,0) | | 1, 0 2 x x x x x x x f x f 故 (0,0) x f 不存在。由 x, y 的对称性, (0,0) y f 不存在。从而, f (x, y) 在 (0,0) 点不可微(否则, (0,0) x f , (0,0) y f 均存在)。 例 3 + = + + + = 0, 0 , 0 1 ( )sin ( , ) 2 2 2 2 2 2 2 2 x y x y x y x y f x y 0 1 sin lim ( ,0) (0,0) (0,0) lim 2 2 0 0 = = − = → → x x x x f x f f x x x , 由 x, y 的对称性, f y (0,0) = 0 。 2 2 ( , ) (0,0) (0,0) (0,0) x y f x y f f x f y x y + − − − 0 1 sin 1 ( )sin 2 2 2 2 2 2 2 2 2 2 → + = + + + + = x y x y x y x y x y ( 0 0 → → y x ) 故 f (x, y) 在 (0,0) 点可微。且 df (0,0) = f x (0,0)dx + f y (0,0)dy = 0 + = + + + − = + 0, 0 , 0 1 cos 1 2 2 sin ( , ) 2 2 2 2 2 2 2 2 2 2 x y x y x y x y x x y x f x y x 取点列 ( , ) n n n P x y , n xn 2 1 = , yn = 0 ,显然 P (x , y ) → (0,0)(n → ) n n n f (x , y ) = −2 2n cos2n → −(n → ) x n n 故 lim ( , ) 0 0 f x y x y x → → 不存在,从而 f (x, y) x 在 (0,0) 点不连续。由 x, y 的对称性, f (x, y) y
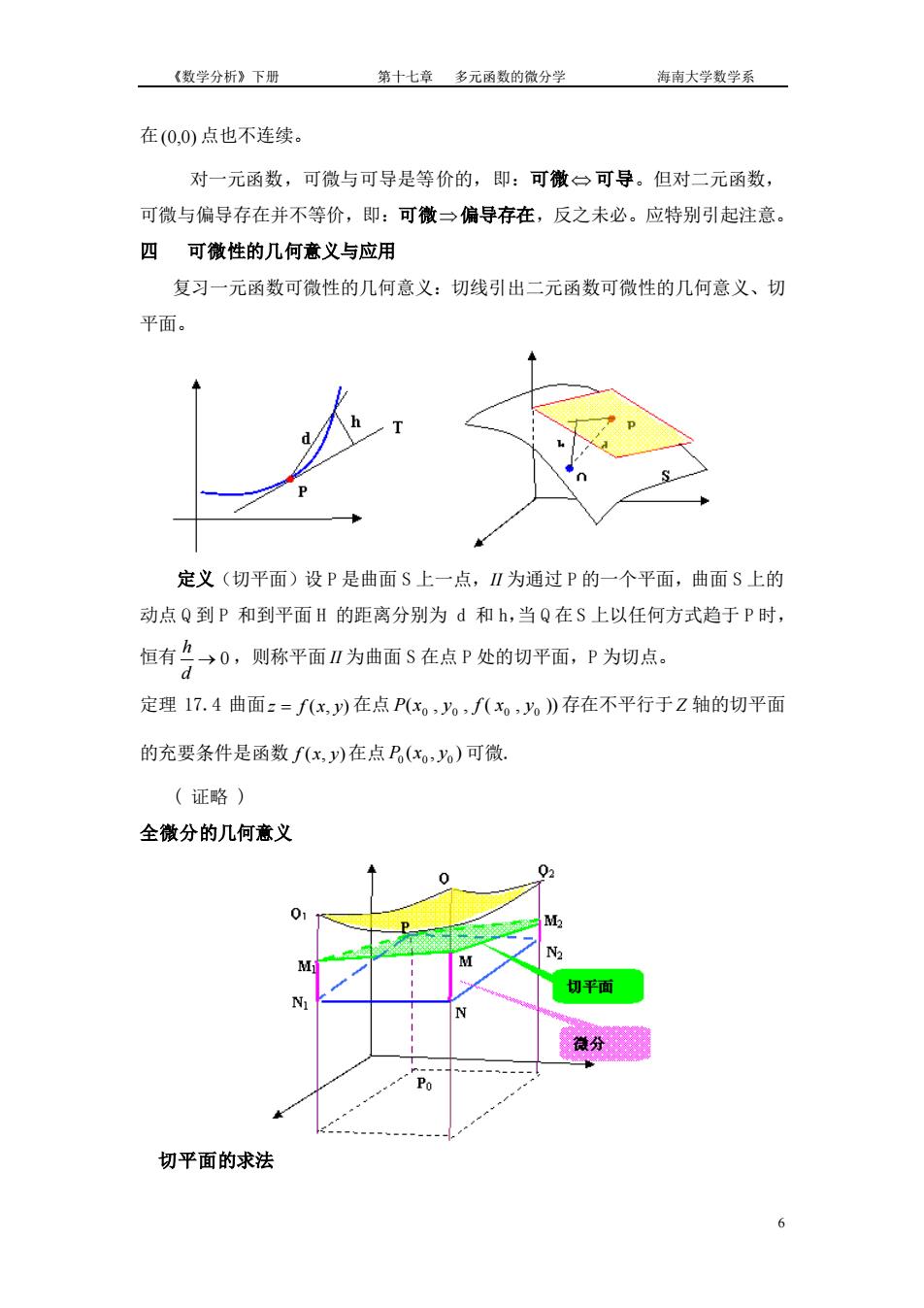
《数学分析》下册 第十七章多元函数的微分学 海南大学数学系 在(0,0)点也不连续。 对一元函数,可微与可导是等价的,即:可微一可导。但对二元函数, 可微与偏导存在并不等价,即:可微一偏导存在,反之未必。应特别引起注意 四可徽性的几何意义与应用 复习一元函数可微性的几何意义:切线引出二元函数可微性的几何意义、切 平面。 定义(切平面)设P是曲面S上一点,Ⅱ为通过P的一个平面,曲面S上的 动点Q到P和到平面H的距离分别为d和h,当Q在S上以任何方式趋于P时, 恒有么→0,则称平面Ⅱ为曲面S在点P处的切平面,P为切点. 定理17.4曲面:=fx,)在点P(x。,。,f(x。,》存在不平行于Z轴的切平面 的充要条件是函数f(x,y)在点P(xo,y%)可微. (证略) 全微分的几何意义 0 切平面 N. 分 切平面的求法
《数学分析》下册 第十七章 多元函数的微分学 海南大学数学系 6 在 (0,0) 点也不连续。 对一元函数,可微与可导是等价的,即:可微 可导。但对二元函数, 可微与偏导存在并不等价,即:可微 偏导存在,反之未必。应特别引起注意。 四 可微性的几何意义与应用 复习一元函数可微性的几何意义:切线引出二元函数可微性的几何意义、切 平面。 定义(切平面)设 P 是曲面 S 上一点, II 为通过 P 的一个平面,曲面 S 上的 动点 Q 到 P 和到平面 H 的距离分别为 d 和 h,当 Q 在 S 上以任何方式趋于 P 时, 恒有 0 h d → ,则称平面 II 为曲面 S 在点 P 处的切平面,P 为切点。 定理 17.4 曲面 z = f (x, y) 在点 ( , , ( , )) 0 0 0 0 P x y f x y 存在不平行于 Z 轴的切平面 的充要条件是函数 f (x, y) 在点 ( , ) 0 0 0 P x y 可微. ( 证略 ) 全微分的几何意义 切平面的求法

《微学分析》下册 第十七章多元函数的微分学 海南大学数学系 设函数fx,)在点Bx)可微,则曲面:=fx,y)在点 P(x。,y。,fx。,%》处的切平面方程为(其中。=fxo,%))) 2-50=∫(x0,gx-xo)+∫(x0%y-o), 法线方向数为±(f(x%),∫,xo%),-1), 法线方程为 x-Xo y-%=-0 f(x%)f(x0%)-1 例1试求抛物面:=a2+br2在点M(x0,o,5o)处的切平面方程和法线 方程. 作近似计算和误差估计: 与一元函数对照,原理. 例2求1.08396的近似值. 例3应用公式5=bsmC计算某三角形面积。现测得a=1250, a=12.50,b=830,C=30°.若测量a,b的误差为±0.01,C的误差为±0.°· 求用此公式 计算该三角形面积时的绝对误差限与相对误差限. 作业教材P117:1-13
《数学分析》下册 第十七章 多元函数的微分学 海南大学数学系 7 设函数 f (x, y) 在 点 ( , ) 0 0 0 P x y 可 微 ,则曲面 z = f (x, y) 在 点 ( , , ( , )) 0 0 0 0 P x y f x y 处的切平面方程为 ( 其中 ( , ) 0 0 0 z = f x y ) ( , )( ) ( , )( ) 0 0 0 0 0 0 0 z z f x y x x f x y y y − = x − + y − , 法线方向数为 ( ( , ) , ( , ) , 1 ) f x x0 y0 f y x0 y0 − , 法线方程为 ( , ) ( , ) 1 0 0 0 0 0 0 0 − − = − = − z z f x y y y f x y x x x y . 例 1 试求抛物面 2 2 z = ax + by 在点 ( , , ) 0 0 0 M x y z 处的切平面方程和法线 方程 . 作近似计算和误差估计: 与一元函数对照, 原理 . 例 2 求 3.96 1.08 的近似值. 例 3 应用公式 S absin C 2 1 = 计算某三角形面积 . 现测得 a =12.50 , a =12.50 , b = 8.30 , C = 30 . 若测量 a , b 的误差为 0.01, C 的误差为 0.1 . 求用此公式 计算该三角形面积时的绝对误差限与相对误差限. 作业 教材 P117:1-13