海南大学：《数学分析》课程教学资源（教案讲义）第二十一章 二重积分 21.4 二重积分的变量变换

《数学分析》下册 第二十一章二重积分 海南大学数学系 §4二重积分的变量变换 教学目的了解二重积分的一般的变量变换公式，学握用极坐标计算二重积分. 教学内容二重积分的一般的变量变换公式：极坐标变换公式。 (①)基本要求：了解二重积分的一般的变量变换公式，掌握二重积分的极坐 标变换。 (2)较高要求：理解二重积分的一般的变量变换公式的证明。 教学建议 (1)本节的重点是极坐标变换公式，要求学生必须熟练掌握。 (2)本节的难点是二重积分的一般的变量变换公式的证明，可要求较好学生 了解。 教学程序 一、二重积分的变量变换公式 引理设变换T:x=u,),y=u,)将m平面上由按段光滑封闭曲线所 围成的闭区域△，一对一地映成y平面上的闭区域D,函数x=xu,),y=u,) 在△内分别具有一阶连续偏导数且它们的函数行列式 ax.y) Ju-atu可+0，u,e4, 则区域的面积 D)S.vya .(5) 正明现给出y=,)在△内分别具有二阶连续偏导数时的证明， y=,)在△内分别具有一阶连续偏导数的证明以后给出. 由于变换T是一对一的，且，刊≠0，因而T把△的内点变为D的内点， 所以△的按段光滑边界曲线L变换到D时，其边界曲线L如也是按段光滑曲线， 设曲线L的参数方程为 u=40),v=r)(a≤1≤B) 由于L按段光滑，所以价，v日在口，上至多除去有限个第一类间断点外

《数学分析》下册 第二十一章 二重积分 海南大学数学系 1 §4 二重积分的变量变换 教学目的 了解二重积分的一般的变量变换公式，掌握用极坐标计算二重积分． 教学内容 二重积分的一般的变量变换公式；极坐标变换公式． (1) 基本要求：了解二重积分的一般的变量变换公式，掌握二重积分的极坐 标变换． (2) 较高要求：理解二重积分的一般的变量变换公式的证明． 教学建议 (1) 本节的重点是极坐标变换公式，要求学生必须熟练掌握． (2) 本节的难点是二重积分的一般的变量变换公式的证明，可要求较好学生 了解． 教学程序 一、二重积分的变量变换公式 引理 设变换 T ：x = x(u,v)，y = y(u,v) 将 uv 平面上由按段光滑封闭曲线所 围成的闭区域  ，一对一地映成 xy 平面上的闭区域 D ，函数 x = x(u,v)，y = y(u,v) 在  内分别具有一阶连续偏导数且它们的函数行列式 J(u,v)= ( ) (u v) x y , ,    0，(u,v)   ， 则区域的面积 (D)= J (u v)dudv   , . （5） 证明 现给出 y = y(u,v) 在  内分别具有二阶连续偏导数时的证明， y = y(u,v) 在  内分别具有一阶连续偏导数的证明以后给出． 由于变换 T 是一对一的，且 J(u,v)  0，因而 T 把  的内点变为 D 的内点， 所以  的按段光滑边界曲线 L 变换到 D 时，其边界曲线 LD 也是按段光滑曲线， 设曲线 L 的参数方程为 u = u(t)，v = v(t) (  t  )． 由于 L 按段光滑，所以 u (t)，v (t) 在 , 上至多除去有限个第一类间断点外

《数学分析》下所 第二十一章二重积分] 海市大学数学系 在其他点上都是连续的.因为Ln=T亿)，所以LD的参数方程为： x=x)=xu》y=0)=tt(a≤1≤B). 若规定1从α变B到时，对应于Lo的正向，则根据格林公式，取 Px,y)=0,0x,y=x,有 Ao.fw-joo-了，02t0-g-0n 另一方面，在w平面上 fa8+g]jtte)2o0+来r0h =a (7) 其中正号及负号分别由1从a变B到时，是对应于Ln的正向或是负方向所决 定.由(6)及(7)得到 0±信血+±2加+喂 令小地，哈。小=哈在平面m上对上式应用格林会式， 得到 40 由于西黄一水小有二所琴数.甲有盖-品，因先 ao ap =J(u,v) 于是 4o)s±广hd 又因为(D)总是非负的，而仙，)在△上不为零且连续，故其函数值△在上不变 号，所以o.ekh 定理21.13设心川在有界闭区域D上可积，变换T:x=仙)

《数学分析》下册 第二十一章 二重积分 海南大学数学系 2 在其他点上都是连续的．因为 ( ) LD = T L ，所以 LD 的参数方程为: x = x(t) = x(u(t),v(t)), y = (t) = y(u(t),v(t)), (  t  )． 若规定 t 从  变  到时，对应于 LD 的正向，则根据格林公式，取 P(x, y) = 0,Q(x, y) = x ，有 (D)= xdy x(t)y (t)dt LD =      = ( ( ) ( )) ( ) v (t) dt v y u t u y x u t v t            +     , , （6） 另一方面，在 uv 平面上 ( )           +   L dv v y du u y x u,v =  ( ( ) ( )) ( ) v (t) dt v y u t u y x u t v t            +     , , （7） 其中正号及负号分别由 t 从  变  到时，是对应于 LD 的正向或是负方向所决 定．由（6）及（7）得到 (D)=  ( )           +   L dv v y du u y x u,v =  ( ) ( )     +   L dv v y du x u v u y x u,v , ． 令 ( ) ( ) u y P u v x u v   , = , ， ( ) ( ) v y Q u v x u v   , = , 在平面 uv 上对上式应用格林公式， 得到 (D)=            −   dudv v P u Q 由于函数 y = y(u,v) 具有二阶连续偏听偏信导数，即有 v u y u v y    =    2 2 ，因此 v P u Q   −   = J(u,v)， 于是 (D)=  ( )   J u,v dudv ． 又因为 (D) 总是非负的，而 J(u,v) 在  上不为零且连续，故其函数值  在上不变 号，所以 (D)= J (u v)dudv   , ． 定理 21.13 设 f (x, y) 在有界闭区域 D 上可积，变换 T ： x = x(u,v)

《数学分析》下册 第二十一章二重积分 海南大学数学系 y=,以将m平面上由按段光滑封闭曲线所围成的闭区域△一对一地映成少 平面上的闭区域D,函数x=,以，y=刊在△内分别具有一阶连续偏导数 且它们的函数行列式 x,) Ju,-atu,可≠0，u,eA, 则 ∬r达迹ftu以ukih 证明用曲线网△把分成n个小区域△，在变换T作用下区域D也相应地分 成个n小区域D,记△，及D,的面积为4A,)及4(D,)=L,)由引理及二重积 分的中值定理，有 do).ah6la). 其中，)e△，f=1m.令=x,n=y6,小，则传，n,)eD.作 二重积分(，)的积分和 2n4o)2t.b6.i6.ia 上式右边的和式是上的可积函数心以，v,以的积分和。又由变换T的 连续性可知，当区域△的分割的细度P→0时，区域D相应的分制的细度T 也趋于零.因此得到 ∬fek∬/u以u,咖 例1求 ,其中D是由x=0,y=0,x+y=1所围区域， 解作变换u=-男=+y即-如+以y=北-川则0 etw 3

《数学分析》下册 第二十一章 二重积分 海南大学数学系 3 y = y(u,v) 将 uv 平面上由按段光滑封闭曲线所围成的闭区域  一对一地映成 xy 平面上的闭区域 D ，函数 x = x(u,v)， y = y(u,v) 在  内分别具有一阶连续偏导数 且它们的函数行列式 J(u,v)= ( ) (u v) x y , ,    0，(u,v)   ， 则 ( )  D f x, y dxdy = ( ( ) ( )) ( )   f x u,v , y u,v J u,v dudv ． 证明 用曲线网  把分成 n 个小区域 i ，在变换 T 作用下区域 D 也相应地分 成个 n 小区域 Di ，记 i 及 Di 的面积为 ( )  i 及 ( )  Di (i =1,  ,n) 由引理及二重积 分的中值定理，有 ( )  Di = J (u v)dudv i   , = J (ui ,vi) ( )  i , 其中 (ui ,vi) i (i =1,  ,n)．令 x  i = (ui ,vi)， y i = (ui ,vi) ，则 ( )  i i ,  Di ．作 二重积分 f (x, y) 的积分和  =  ( ) ( ) = n i i i Di f 1  ,  =  ( ( ) ( )) ( ) ( ) =  n i i f x ui vi y ui vi J ui vi 1 , , , ,  , 上式右边的和式是上的可积函数 f (x(u,v), y(u,v)) J(u,v) 的积分和．又由变换 T 的 连续性可知，当区域  的分割的细度 T → 0 时，区域 D 相应的分割的细度 TD 也趋于零．因此得到 ( )  D f x, y dxdy = ( ( ) ( )) ( )   f x u,v , y u,v J u,v dudv ． 例 1 求  + − D x y x y e dxdy ，其中 D 是由 x = 0, y = 0, x + y = 1 所围区域. 解 作变换 u = x − y,v = x + y 即 x = (u + v) y = (v − u) 2 1 , 2 1 ,则 J(u,v)= 0 2 1  ,  + − D x y x y e dxdy =   e  dudv v u 2 1 =   − 1 0 2 1 dv e du v v v u =   − 1 0 2 1 dv e du v v v u = ( ) 2 4 1 1 1 0 1 − − − − =  e e v e e dv

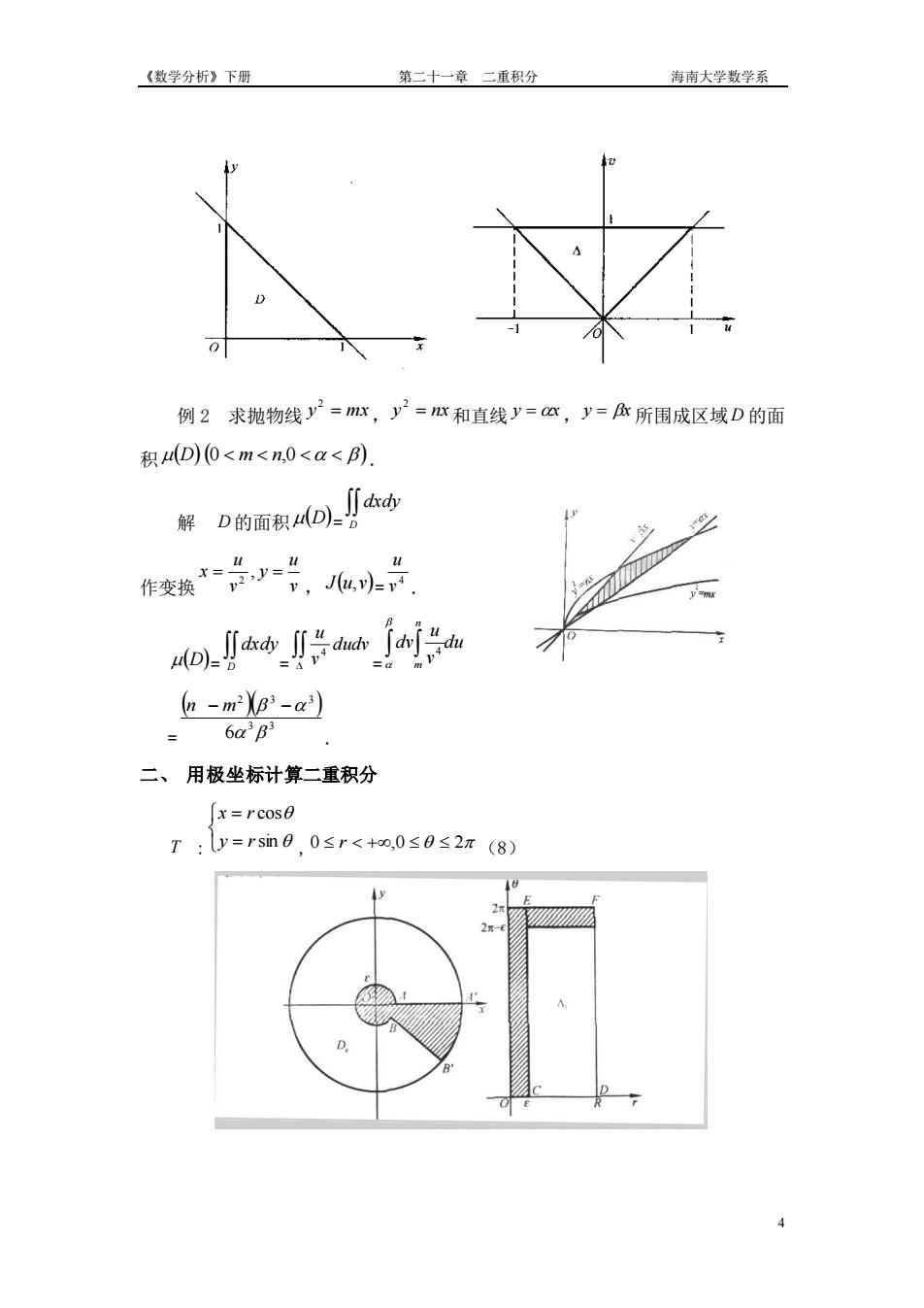
《数学分析》下册 第二十一章二重积分 海市大学数学系 例2求抛物线y=mx,y=心和直线y=心，y=卧所围成区域D的面 积(D)0<m<n,0<a<). 解D的面积O):厂 do.∬.rgtf时a a-mYe-a) =6a3B3 二、用极坐标计算二重积分 [x=rcos0 T:y=rsn0,0≤r<+o,0≤0≤2π(8)

《数学分析》下册 第二十一章 二重积分 海南大学数学系 4 例 2 求抛物线 y = mx 2 ，y = nx 2 和直线 y = x，y = x 所围成区域 D 的面 积 (D) (0  m  n,0   )． 解 D 的面积 (D)=  D dxdy 作变换 v u y v u x = , = 2 ， J(u,v)= 4 v u . (D)=  D dxdy =   dudv v u 4 =     du v u dv n m 4 = ( )( ) 3 3 2 3 3 6  n − m  − . 二、 用极坐标计算二重积分 T :    = =   sin cos y r x r , 0  r  +,0    2 （8）

《数学分析》下所 第二十一章二重积分 海南大学数学系 定理21.14设/代，川满足定理21.13的条件，且在极坐标变换(8)下， xy平面上有界区域D与r0平面上区域△对应，则成立 ∬f6klkw∬fros8,rsin0dr0 正明若D为圆城《在小2+广≤R},则A为9平面上的矩形区域 0,x02].设D为在圆环，p0.于是由定理21.13有 ∬/lddy ff(reoso,rsno)daB 因为x,以在有界闭区域D上有界，在上式中令￡→0即得 (dy f(rcos0.rsin ordrdo 若D是一般的有界区域，则取足够大的R>0,使D包含在圆域 D.ysR 内，并且在DR上定义函数 ∫fxy以(xy)eD f(x,y)=1o.(x.y)eD (i)若原点OED,y平面上射线日=常数与D的边界至多交于两点.△表 示为《O)sr≤⑧a≤0≤B,于是有 le) 若原点O任D,xy平面上的圆r=常数与D的边界至多交于两点， △表示为A)s0≤8，斯≤r≤5，于是有 ∬r(x.yybrdy frdr了frcos0,.rsin 0)o

《数学分析》下册 第二十一章 二重积分 海南大学数学系 5 定理 21.14 设 f (x, y) 满足定理 21．13 的条件，且在极坐标变换（8）下， xy 平面上有界区域 D 与 r 平面上区域  对应，则成立 ( )  D f x, y dxdy = ( )   f r cos,rsin  rdrd . 证明 若 D 为圆域 ( )  2 2 2 x, y x + y  R ，则  为 r 平面上的矩形区域 0,R0,2 ．设 D 为在圆环 ( )  2 2 2 2 x, y 0    x + y  R 中除去中心角为  的扇 形 BBAA 所得的区域，则在变换（8）下， D 对应于平面上的矩形区域  = ,R0,2 − ．但极坐标变换（8）在 D 与  之间是一对一变换，且  在 上函数行列式 J(r, )  0 ．于是由定理 21．13 有 ( )  D f x, y dxdy = ( )   f r cos ,rsin  rdrd ， 因为 f (x, y) 在有界闭区域 D 上有界，在上式中令  →0 即得 ( )  D f x, y dxdy = ( )   f r cos,rsin  rdrd . 若 D 是一般的有界区域，则取足够大的 R  0 ，使 D 包含在圆域 DR = ( )  2 2 2 x, y x + y  R 内，并且在 DR 上定义函数 f (x, y)= ( ) ( )  ( )     x y D f x y x y D 0, , , , , ， （ⅰ）若原点 OD, xy 平面上射线  =常数与 D 的边界至多交于两点. 表 示为 r1 ( )  r  r2 ( ),    ，于是有 ( )  D f x, y dxdy = ( ) ( ) ( )          2 1 cos , sin r r d f r r rdr . 若原点 OD, xy 平面上的圆 r =常数与 D 的边界至多交于两点．  表示为 ( ) ( ) 1 2 1 2  r   r ,r  r  r ，于是有 ( )  D f x, y dxdy = ( ) ( ) ( )   2 1 2 1 cos , sin r r r r rdr f r r d      ．

《数学分析》下册 第二十一章二重积分] 海市大学数学系 (ⅱ)若原点O为D的内点，D的边界方程表示为r=⊙)，则 △表示为0≤r≤r0)0≤0≤2π，于是有 th.ao了l-cs0.rsn0hir =00 (出)若原点O在D的边界上，则△为 0≤r≤r0)a≤0≤B」 于是有 jkhs了jdoJrcom0.o 1 ，其中为圆域2+少2s1 例4球+少+：子=R被圆柱面之+少=所割下部分的体积

《数学分析》下册 第二十一章 二重积分 海南大学数学系 6 （ⅱ）若原点 O 为 D 的内点， D 的边界方程表示为 r = r( ) ，则  表示为 0  r  r( ),0   2 ，于是有 ( )  D f x, y dxdy = ( ) ( )        2 0 0 cos , sin r d f r r rdr . （ⅲ）若原点 O 在 D 的边界上，则  为 0  r  r( ),    ， 于是有 ( )  D f x, y dxdy = ( ) ( )         r d f r r rdr 0 cos , sin . 例 3 计算 I =  D − − d x y  2 2 1 1 ，其中为圆域 1 2 2 x + y  . 解  D − − d x y  2 2 1 1 =   −   2 0 1 0 2 1 dr r r d =    − −   2 0 2 0 1 1 r d =    2 0 d = 2 . 例 4 球 2 2 2 2 x + y + z = R 被圆柱面 x + y = Rx 2 2 所割下部分的体积．

《数学分析》下册 第二十一章二重积分】 海南大学数学系 解rr-r加 ja0了re-rt4Rj6-snoH =40 =3 后-引 例6计算1广ea ,其中D为圆域：x2+y2≤R ,了0e女-e。扩义极坐标变换 解1=00 x=arcose T:y=brsn0,0≤r<+o0≤0≤2x J(r,0)=abr ,广义极坐标变换 6aooi-Fob.音 V=80 当a=6=c=R时得到球的体积为风 作业P242:1-8

《数学分析》下册 第二十一章 二重积分 海南大学数学系 7 解 V =4  − − D R x y d 2 2 2 =4   − 2 0 cos 0 2 2    R d R r rdr = 3 3 4 R ( )  − 2 0 3 1 sin   d =       − 3 2 3 2 4 3  R . 例 5 计算 I = ( )  − + D x y e d 2 2 ，其中 D 为圆域： 2 2 2 x + y  R 解 I =   −   2 0 0 2 R r d re dr = ( ) 2 1 R e −  − ，作广义极坐标变换 T :    = =   sin cos y br x ar , 0  r  +,0    2 ， J(r, ) = abr ， 例 6 求椭球体 1 2 2 2 2 2 2 + +  c z b y a x 的体积. 解 V =8  − − D dxdy b y a x c 2 2 2 2 1 ,广义极坐标变换 V =8   − 2 0 1 0 2 1  d c r abrdr = abc 3 4 ， 当 a = b = c = R 时得到球的体积为 3 3 4  R . 作业 P242: 1-8