
第八章λ一矩阵 §1λ一矩阵§2一矩阵初等变换下的标准形 教学目标:掌握λ一矩阵、λ一矩阵的初等变换、λ一矩阵初等变换下的标准形的概念,λ一矩 阵可逆的充要条件,标准形的求法。 教学重点:λ一矩阵初等变换下的标准形的求法。 教学方法:讲授法. 教学过程: §1λ一矩阵 设P是一个数域,是一个文字.若一个矩阵的元素均属于P[],则称此矩阵为λ一矩阵,因为 PCP[],故通常所说P上矩阵也是λ一矩阵.为了区别起见,P上矩阵称为数字矩阵.今后用 A(1),B(1)等表示λ一矩阵 与数字矩阵一样λ一矩阵也有加法、乘法运算,并且有与数字矩阵相同的算律.同样n×n,λ— 矩阵也有行列式的概念,并与数字矩阵的行列式有相同的性质.利用行列式,可定义一矩阵的子式, 由此可得 定义1若λ一矩阵A()有一个r(r≥1)级子式不为零,而所有r+1级子式(若存在的话)全为 零,则称A()的秩为r.规定零矩阵的秩为零 定义2设A()为矩阵,若存在n×nλ一矩阵B()使 A(1)B(2)=B(1)A(λ)=E (1) 则称A(1)可逆.而B()就称为A()的逆矩阵,记为A-1() 定理1n级矩阵A(λ)可逆0≠|A(λ)∈P 证明若A()可逆,则有B()使(1)式成立.两边取行列式得 |A(λ)}|B(λ)|=|E|=1 上式表明A(1)是P[1]中的零次多项式,即P中非零数
第八章 —矩阵 §1 —矩阵 §2 —矩阵初等变换下的标准形 教学目标: 掌握 —矩阵、 —矩阵的初等变换、 —矩阵初等变换下的标准形的概念, —矩 阵可逆的充要条件,标准形的求法。 教学重点: —矩阵初等变换下的标准形的求法。 教学方法: 讲授法. 教学过程: §1 —矩阵 设 P 是一个数域,是一个文字.若一个矩阵的元素均属于 P ,则称此矩阵为 —矩阵,因为 P P ,故通常所说 P 上矩阵也是 —矩阵.为了区别起见, P 上矩阵称为数字矩阵.今后用 A B ( ), ( ) 等表示 —矩阵 与数字矩阵一样 —矩阵也有加法、乘法运算,并且有与数字矩阵相同的算律.同样 n n , — 矩阵也有行列式的概念,并与数字矩阵的行列式有相同的性质.利用行列式,可定义 —矩阵的子式, 由此可得 定义 1 若 —矩阵 A( ) 有一个 r r( 1) 级子式不为零,而所有 r +1 级子式(若存在的话)全为 零,则称 A( ) 的秩为 r .规定零矩阵的秩为零. 定义 2 设 A( ) 为矩阵,若存在 n n —矩阵 B( ) 使 A B B A E ( ) ( ) ( ) ( ) = = (1) 则称 A( ) 可逆.而 B( ) 就称为 A( ) 的逆矩阵,记为 1 A ( ) − . 定理 1 n 级矩阵 A( ) 可逆 0 ( ) A P . 证明 若 A( ) 可逆,则有 B( ) 使(1)式成立.两边取行列式得 A B E ( ) ( ) 1 = = 上式表明 A( ) 是 P中的零次多项式,即 P 中非零数

反之,若d=A(2)是P中非零数,令A'()表4()的伴随矩阵,则它也是入一矩阵由于 A.4'a-'a.4a=E d d 故A(2)可逆 $2入一矩阵初等变换下的标准形 定义3以下变换叫做入一矩阵的初等变换: (1)交换矩阵的两行(列): (2)用非零数c乘矩阵的某一行(列): (3)将矩阵某一行(列)的(2)倍加到另一行(列),这是()∈P[ 和数字矩阵一样,对应上述三种初等变换,也可引进初等矩阵,分别记为P亿,),PG(c》P亿,j(()》 其作用也和数字阵中的初等矩阵相同初等矩阵均可逆且 P'6,)=P6,),P-'(ic》=Pi(白》P-'Gjoa》=P6j0a》 为了简便,今后用记号[,小表示交换1,j两行(列[(c]表示用c≠0乘i行(列):[i+j(p]表示把j 行列的(2)倍加到1行(列). 定义4若经一系列初等变换可将A)化为B(),则称A()与B()等价 易知等价关系且有反身性、对称性与传递性利用初等变换与初等矩阵的关系可得,A()与B()等 价的充要条件是有一系列初等矩阵B,B,.,P,2,22,.,2使 A()=R,B,.,PB(2)g,O2,.,g (0) 本节将证明任意一个入一矩阵都可经初等变换化为某种对角形.为此,先证 引理设A()的左上角元素a,(2)≠0.并且A()至少有一个元素不被它整除.那么必有与 4)等价的矩阵B(),它的左上角元素也不为零,但次数比a,()的次数低 证明4()的第一列中有一个元素a()不能被4(2)整除,则 aa(2)=a,(a)q)+r(2),r()≠0,(a)<a(a,(2) 对A()作下列初等行变换:
反之,若 d A = ( ) 是 P 中非零数,令 A ( ) 表 A( ) 的伴随矩阵,则它也是 —矩阵.由于 ( ) ( ) ( ) ( ) A A A A E d d = = 故 A( ) 可逆. §2 —矩阵初等变换下的标准形 定义 3 以下变换叫做 —矩阵的初等变换: (1) 交换矩阵的两行(列); (2) 用非零数 c 乘矩阵的某一行(列); (3) 将矩阵某一行(列)的 ( ) 倍加到另一行(列),这是 ( ) . P 和数字矩阵一样,对应上述三种初等变换,也可引进初等矩阵,分别记为 P i j P i c ( , ), ( ( )) P i j ( , ( ( ))) 其作用也和数字阵中的初等矩阵相同.初等矩阵均可逆且 1 1 1 1 P i j P i j P i c P i P i j P i j ( , ) ( , ), ( ( )) ( ( )), ( , ( ( ))) ( , ( ( ))) c − − − = = = 为了简便,今后用记号 i j , 表示交换 i j , 两行(列). i c( ) 表示用 c 0 乘 i 行(列); i j + ( ) 表示把 j 行(列)的 ( ) 倍加到 i 行(列). 定义 4 若经一系列初等变换可将 A( ) 化为 B( ) ,则称 A( ) 与 B( ) 等价. 易知等价关系且有反身性、对称性与传递性.利用初等变换与初等矩阵的关系可得, A( ) 与 B( ) 等 价的充要条件是有一系列初等矩阵 1 2 1 2 , , , , , , , P P P Q Q Q s t 使 1 2 1 2 ( ) , , , ( ) , , , A P P P B Q Q Q = s t (1) 本节将证明任意一个 —矩阵都可经初等变换化为某种对角形.为此,先证 引理 设 A( ) 的左上角元素 11 a ( ) 0 .并且 A( ) 至少有一个元素不被它整除.那么必有与 A( ) 等价的矩阵 B( ) ,它的左上角元素也不为零,但次数比 11 a ( ) 的次数低. 证明 A( ) 的第一列中有一个元素 1 ( ) i a 不能被 11 a ( ) 整除,则 1 11 11 ( ) ( ) ( ) ( ), ( ) 0, ( ( )) ( ( ))) i a a q r r r a = + . 对 A( ) 作下列初等行变换:
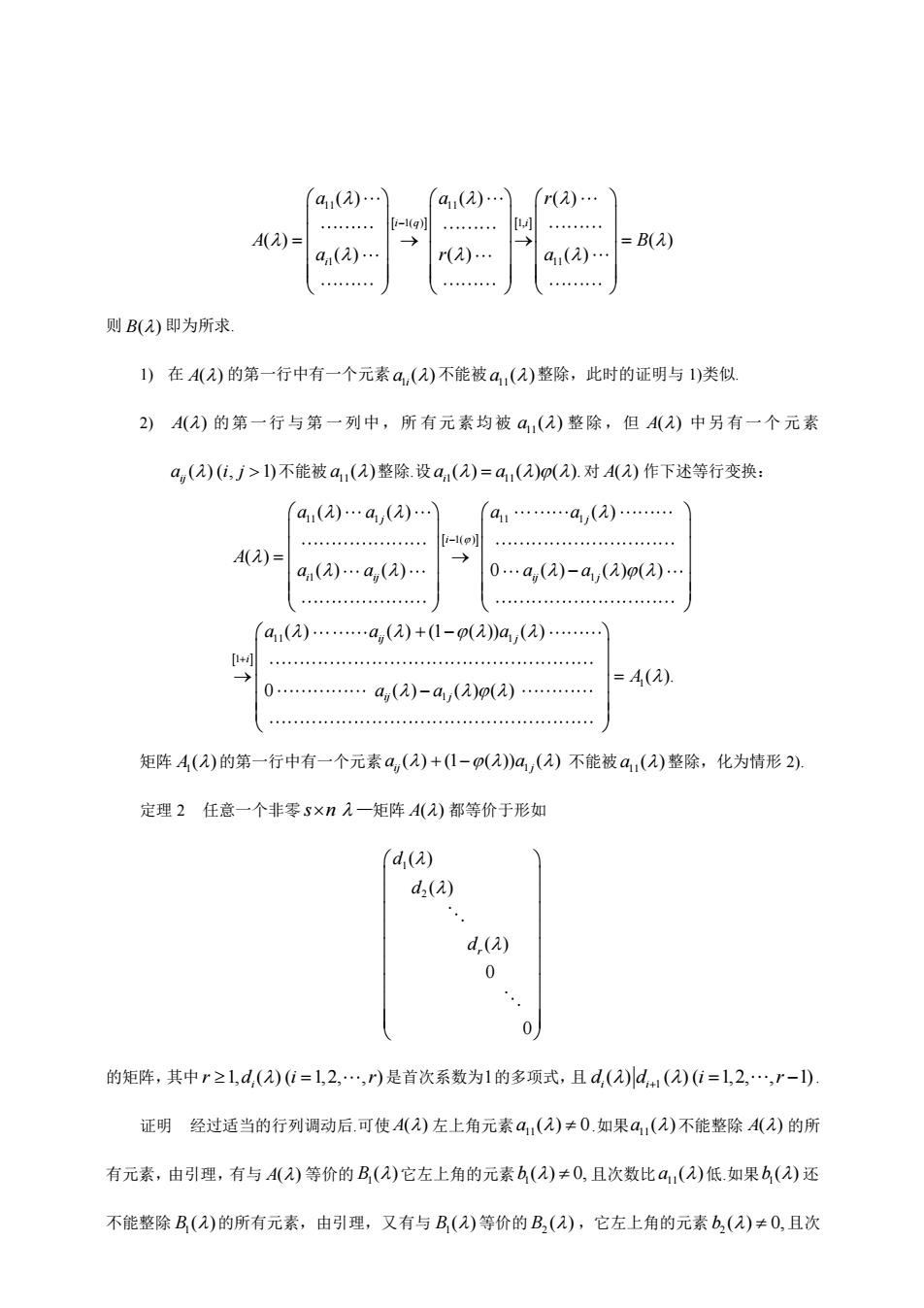
a(). a().)r().) 4A)= =B(2) a(2). r(2). a(2). 则B()即为所求 1)在A()的第一行中有一个元素a,()不能被a,(2)整除,此时的证明与1)类似 2)A()的第一行与第一列中,所有元素均被4,()整除,但A)中另有一个元素 a,(2)(,j广>)不能被a,(a)整除设a(2)=a,()(2).对A(2)作下述等行变换 a(2).a(a).) a.a,(2). 4A(2)= a().a,(2) 0.a,()-a,((2) a(2).a(2)+(1-p()a(2).】 =A(a). 0.a,(2)-a(a0p(2). 矩阵A()的第一行中有一个元素a,(a)+(1-p)a,()不能被a,(2)整除,化为情形2) 定理2任意一个非零s×n入一矩阵A()都等价于形如 d,(a) d2(2) d.(a) 0 0 的矩阵,其中r21,d,(2)0=1,2,.,r)是首次系数为1的多项式,且d()d(2)(i=1,2,.,r-1) 证明经过适当的行列调动后.可使A()左上角元素a,(2)≠0.如果a,(2)不能整除A()的所 有元素,由引理,有与A2)等价的B()它左上角的元素b(a)≠0,且次数比a,()低如果6()还 不能整除B(2)的所有元素,由引理,又有与B,()等价的B,(),它左上角的元素b,()≠0,且次
11 11 1( ) 1, 1 11 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) i q i i a a r A B a r a − = → → = 则 B( ) 即为所求. 1) 在 A( ) 的第一行中有一个元素 1 ( ) i a 不能被 11 a ( ) 整除,此时的证明与 1)类似. 2) A( ) 的第一行与第 一列中,所 有元素均被 11 a ( ) 整除,但 A( ) 中另有一个 元素 ( ) ( , 1) ij a i j 不能被 11 a ( ) 整除.设 1 11 ( ) ( ) ( ). i a a = 对 A( ) 作下述等行变换: 11 1 11 1 1( ) 1 1 11 1 1 ( ) ( ) ( ) ( ) ( ) ( ) 0 ( ) ( ) ( ) ( ) ( ) (1 ( )) ( ) 0 j j i i ij ij j ij j i i a a a a A a a a a a a a a − + = → − + − → 1 1 ( ). ( ) ( ) ( ) j j A a = − 矩阵 1 A ( ) 的第一行中有一个元素 1 ( ) (1 ( )) ( ) ij j a a + − 不能被 11 a ( ) 整除,化为情形 2). 定理 2 任意一个非零 s n —矩阵 A( ) 都等价于形如 1 2 ( ) ( ) ( ) 0 0 r d d d 的矩阵,其中 1, ( ) ( 1,2, , ) i r d i r = 是首次系数为 1 的多项式,且 1 ( ) ( ) ( 1,2, , 1) i i d d i r + = − . 证明 经过适当的行列调动后.可使 A( ) 左上角元素 11 a ( ) 0 .如果 11 a ( ) 不能整除 A( ) 的所 有元素,由引理,有与 A( ) 等价的 1 B ( ) 它左上角的元素 1 b ( ) 0, 且次数比 11 a ( ) 低.如果 1 b ( ) 还 不能整除 1 B ( ) 的所有元素,由引理,又有与 1 B ( ) 等价的 2 B ( ) ,它左上角的元素 2 b ( ) 0, 且次

数比b(2)低如此继续进行下去因a(a)的次数有限,有限步之后,必有B,(a)与A()等价.它左上 角元素b,(2)≠0,且b,(2)整除B,()的所有元素b,()b(2)=b,()q(). 对B,(2)作初等变换 b,().h().】 (b.(2)0 [2-a-0 B,(2) .2-z-(:: A(2) 其中A()中所有元素均被b,()整除,因为它们都是B,()中元素的组合 如果A()≠0,则对A(入)重复以上过程,进而把矩阵化为 d.()0.0Y 0 d(a).0 0 0 A(2) 0 0 (0 0 其中d()与d,(a)都是首次系数为1的多项式(d(a)与b,()只差一个数数倍数),而且 d(2)d4(),d()整除A(a)的所有元素 如此进行下去,4()最后就化成了所要求的形式,它称为A()的标准形 例用初等变换化 (1-元21-1 4)=元2-1 1+22+元-1-2 为标准形 12-1 )12-1元) 10 解:4高02-元→0-元 30- 12+2-1-21-1-2-0-元-2- 10 0-a时10 2 0 0-2232*200-22-元 02 0=B)】 002+
数比 1 b ( ) 低.如此继续进行下去.因 11 a ( ) 的次数有限,有限步之后,必有 ( ) B s 与 A( ) 等价.它左上 角元素 ( ) 0, s b 且 ( ) s b 整除 ( ) B s 的所有元素 ( ); ( ) ( ) ( ). ij ij s ij b b b q = 对 ( ) B s 作初等变换 21 31 12 13 1 2 1( ) , 3 1( ) , 2 1( ) , 3 1( ) , 1 1 ( ) ( ) ( ) 0 0 ( ) ( ) ( ) 0 s j s q q s q q i b b b B b A − − − − = → 其中 1 A ( ) 中所有元素均被 ( ) s b 整除,因为它们都是 ( ) B s 中元素的组合. 如果 1 A ( ) 0 ,则对 1 A ( ) 重复以上过程,进而把矩阵化为 1 2 2 ( ) 0 0 0 ( ) 0 0 0 ( ) 0 0 0 0 d d A 其中 1 d ( ) 与 2 d ( ) 都是首次系数为 1 的多项式( 1 d ( ) 与 ( ) s b 只差一个数数倍数) ,而且 1 2 2 d d d ( ) ( ), ( ) 整除 2 A ( ) 的所有元素. 如此进行下去, A( ) 最后就化成了所要求的形式,它称为 A( ) 的标准形. 例 用初等变换化 2 2 3 2 1 2 1 ( ) 1 1 A − − = − + + − − 为标准形 解: 3 1 2 2 2 1 3 2 1(2 1) 3 2 3 2 3 2 3 1( ) 1 2 1 1 2 1 1 0 0 ( ) 0 0 0 1 1 1 0 A − + − − − − − → − → − → − + − − − − − − − − 3 2( 1) 2( 1) , 3( 1) 2 2,3 3 2( ) 2,3 2 3 2 2 1 0 0 1 0 0 1 0 0 0 0 0 0 0 ( ). 0 0 0 0 0 B − + − − + → − → − → → = − − − − − +

$3不变因子 教学目标掌握行列式因子的概念与性质,不变因子的概念,二入一矩阵等价的充要条件,入一 矩阵可逆的充要条件。 教学重点:行列式因子、不变因子的概念,二入一矩阵等价的充要条件。 教学方法:讲授法。 教学过程: 现在来证明,入一矩阵的标准形是唯一的。首先引入 定义5设元一矩阵4(2)的秩为r,1≤k≤”,A()中全部k阶子式的首项系数为1的最大公因 式D,()称为4()的k阶行列式因子。 定理3等价的入一矩阵具有相同的秩与相同的各阶行列式因子。 证明:我们只需证明,入一矩阵经过一次初等变换,秩与行列式因子是不变的。 设一矩阵A)经过一次行初等变换变成B(),f()与g()分别是4()与B(2)的k阶行 列式因子。我们证明∫=g。下面分三种情形讨论: 1)A()→B()。这时,B()的每个k阶子式或者等于4()的某个k阶子式,或者与 4)的某个k阶子式反号,因此f()是B()的k阶子式的公因式,从而f(2)g()。 2)4()m©1→B()。B()的每个k阶子式或者等于A)的某个k阶子式,或者等于A() 的某个k阶子式的c倍。因此f(a)是B()的k阶子式的公因式,从而f)g()。 3)A()1B)。这时B()中那些包含1行与j行的k阶子式和那些不包含1行与/ 行的k阶子式都等于A()中对应的k阶子式:B()中那些包含i行但不包含j行的k阶子式,按1行
作业: P355,习题 1 之 2),3)。. 预习: 下一节的基本概念. §3 不变因子 教学目标: 掌握行列式因子的概念与性质,不变因子的概念,二 —矩阵等价的充要条件, — 矩阵可逆的充要条件。 教学重点: 行列式因子、不变因子的概念,二 —矩阵等价的充要条件。 教学方法: 讲授法. 教学过程: 现在来证明, —矩阵的标准形是唯一的。首先引入 定义 5 设 —矩阵 A( ) 的秩为 r k r ,1 ,A( ) 中全部 k 阶子式的首项系数为 1 的最大公因 式 ( ) Dk 称为 A( ) 的 k 阶行列式因子。 定理 3 等价的 —矩阵具有相同的秩与相同的各阶行列式因子。 证明: 我们只需证明, —矩阵经过一次初等变换,秩与行列式因子是不变的。 设 —矩阵 A( ) 经过一次行初等变换变成 B( ) ,f ( ) 与 g( ) 分别是 A( ) 与 B( ) 的 k 阶行 列式因子。我们证明 f g = 。下面分三种情形讨论: 1) A( ) ⎯⎯⎯→[ , ] i j B( ) 。这时, B( ) 的每个 k 阶子式或者等于 A( ) 的某个 k 阶子式,或者与 A( ) 的某个 k 阶子式反号,因此 f ( ) 是 B( ) 的 k 阶子式的公因式,从而 f g ( ) ( ) 。 2) A( ) ⎯⎯⎯→ [ ( )] i c B( ) 。B( ) 的每个 k 阶子式或者等于 A( ) 的某个 k 阶子式,或者等于 A( ) 的某个 k 阶子式的 c 倍。因此 f ( ) 是 B( ) 的 k 阶子式的公因式,从而 f g ( ) ( ) 。 3) A( ) ⎯⎯⎯⎯→ [ ( )] i j + B( ) 。这时 B( ) 中那些包含 i 行与 j 行的 k 阶子式和那些不包含 i 行与 j 行的 k 阶子式都等于 A( ) 中对应的 k 阶子式; B( ) 中那些包含 i 行但不包含 j 行的 k 阶子式,按 i 行

分成两部分,而等于4(2)的一个k阶子式与另一个k阶子式的±(2)倍的和。因此f(2)是4()的 k阶子式的公因式,从而f(2)g()。 对于列变换,证明完全一样。总之,如果A()经过一次初等变换变成B(),那么f()g()。 但由初等变换的可逆性,同样可得g(2)/(),于是f()=g(2)。 当A()的k阶子式全部为零时,B()的k阶子式也全部为零:反之亦然。因此,A()与B() 有相同的秩与相同的各阶行列式因子。证毕。 现在来计算标准形矩阵的行列式因子。设标准形为 d(A) d,(a) d,(a) (1) 0 其中d,(2,d,(,.d,()是首项系数为1的多项式,且d()d(2i=l,2,.,r-l).不难看出 在这种形式的矩阵中,如果一个k阶子式包含的行与列的标号不完全相同,那么这个k阶子式一定为 零。因此,为了计算k阶行列式因子,只要看由,占.,4行与,.,4列组成的k阶子式就行了, 而这个k阶子式等于d,(2)d,().d,()。显然,这种k阶子式的最大公因式就是 d(2)d,().d()(k=1,2,.,r). 定理4入一矩阵的标准形是唯一的。 证明设(1)是A()的标准形。由于A()与(1)等价,它们有相同的秩与相同的行列式因 子,因此,4()的秩就是标准形的主对角线上非零元素的个数r:4()的k阶行列式因子就是 D,()=d,(a)d,().d() (2) 于是 4()=D(,d(= D(2) 4(=2 D() (3) 这说明A()的标准形(1)的主对角线上非零元素是被A()的行列式因子所唯一决定的,所以4(2)
分成两部分,而等于 A( ) 的一个 k 阶子式与另一个 k 阶子式的 ( ) 倍的和。因此 f ( ) 是 A( ) 的 k 阶子式的公因式,从而 f g ( ) ( ) 。 对于列变换,证明完全一样。总之,如果 A( ) 经过一次初等变换变成 B( ) ,那么 f g ( ) ( ) 。 但由初等变换的可逆性,同样可得 g f ( ) ( ) ,于是 f g ( ) ( ) = 。 当 A( ) 的 k 阶子式全部为零时, B( ) 的 k 阶子式也全部为零;反之亦然。因此, A( ) 与 B( ) 有相同的秩与相同的各阶行列式因子。证毕。 现在来计算标准形矩阵的行列式因子。设标准形为 1 2 ( ) ( ) ( ) 0 0 r d d d , (1) 其中 1 2 ( ), ( ), ( ) r d d d 是首项系数为 1 的多项式,且 1 ( ) ( )( 1,2, , 1) i i d d i r + = − 。不难看出, 在这种形式的矩阵中,如果一个 k 阶子式包含的行与列的标号不完全相同,那么这个 k 阶子式一定为 零。因此,为了计算 k 阶行列式因子,只要看由 1 2 , , k i i i 行与 1 2 , , k i i i 列组成的 k 阶子式就行了, 而这个 k 阶子式等于 1 2 ( ) ( ) ( ) k i i i d d d 。显然,这种 k 阶子式的最大公因式就是 1 2 ( ) ( ) ( ) k d d d ( 1,2, , ) k r = 。 定理 4 —矩阵的标准形是唯一的。 证明 设(1)是 A( ) 的标准形。由于 A( ) 与(1)等价,它们有相同的秩与相同的行列式因 子,因此, A( ) 的秩就是标准形的主对角线上非零元素的个数 r ; A( ) 的 k 阶行列式因子就是 ( ) Dk = 1 2 ( ) ( ) ( ) k d d d (2) 于是 2 1 1 2 1 1 ( ) ( ) ( ) ( ), ( ) , , ( ) ( ) ( ) r r r D D d D d d D D − = = = 。 (3) 这说明 A( ) 的标准形(1)的主对角线上非零元素是被 A( ) 的行列式因子所唯一决定的,所以 A( )

的标准形是唯一的。正毕。 定义6标准形的主对角线上非零元素d,(2),d,(),.d,()称为元一矩阵A2)的不变因子。 定理5两个入一矩阵等价的充要条件是它们有相同的行列式因子:或者,它们有相同的不变因 子。 证明等式(2)与(3)表明一矩阵的行列式因子与不变因子是相互确定的。因此,两个矩 阵有相同的各阶行列式因子,就有相同的各阶不变因子。 必要性已由定理3证明。 充分性是显然的。事实上,若元一矩阵A()与B()有相同的不变因子,则4()与B()和同 一个标准形等价,因而A(2)与B()等价。证毕。 由(3)可以看出,在1一矩阵的行列式因子之间,有关系 D(aD()(k=l,2,.,r-l). (4) 在计算入一矩阵的行列式因子时,常常先计算最高阶的行列式因子,由(4)便可大致确定低阶 行列式因子的范围了 我们来看可逆矩阵的标准形。设4)为n×n可逆矩阵,由定理1知 4(2)=d≠0。 于是D(2)=1,从而由(4)可知D()=1(k=1,2,.,n),因此 d()=1(k=12.,m). 由此可知,可逆矩阵的标准形是单位矩阵E。反之,与单位矩阵等价的矩阵一定是可逆的,因为它的 行列式是一个非零的数。因此矩阵可逆的充要条件是它与单位矩阵等价。由于A()与B()等价的 充要条件是有一系列初等矩阵R,B,P,Q,Q2,.,Q,使 A()=PE.PB(2)2g2Q, 令B(2)=E,就得到 定理6矩阵A()可逆的充要条件是它可以表示为一些初等矩阵的乘积。 推论两个s×n的元一矩阵A(2)与B()等价的充要条件是,有一个sx5可逆矩阵P(2)与 个n×n可逆矩阵Q(2)使 B()=P(a)AA)Q()。 作业:P357,习题4
的标准形是唯一的。证毕。 定义 6 标准形的主对角线上非零元素 1 2 ( ), ( ), ( ) r d d d 称为 —矩阵 A( ) 的不变因子。 定理 5 两个 —矩阵等价的充要条件是它们有相同的行列式因子;或者,它们有相同的不变因 子。 证明 等式(2)与(3)表明 —矩阵的行列式因子与不变因子是相互确定的。因此,两个矩 阵有相同的各阶行列式因子,就有相同的各阶不变因子。 必要性已由定理 3 证明。 充分性是显然的。事实上,若 —矩阵 A( ) 与 B( ) 有相同的不变因子,则 A( ) 与 B( ) 和同 一个标准形等价,因而 A( ) 与 B( ) 等价。证毕。 由(3)可以看出,在 —矩阵的行列式因子之间,有关系 1 ( ) ( ) ( 1,2, , 1) D D k r k k + = − 。 (4) 在计算 —矩阵的行列式因子时,常常先计算最高阶的行列式因子,由(4)便可大致确定低阶 行列式因子的范围了。 我们来看可逆矩阵的标准形。设 A( ) 为 n n 可逆矩阵,由定理 1 知 A d ( ) 0 = 。 于是 ( ) 1 D n = ,从而由(4)可知 ( ) 1 ( 1,2, , ) D k n k = = ,因此 ( ) 1 ( 1,2, , ) k d k n = = 。 由此可知,可逆矩阵的标准形是单位矩阵 E 。反之,与单位矩阵等价的矩阵一定是可逆的,因为它的 行列式是一个非零的数。因此矩阵可逆的充要条件是它与单位矩阵等价。由于 A( ) 与 B( ) 等价的 充要条件是有一系列初等矩阵 1 2 1 2 , , , , , , , P P P Q Q Q s t ,使 A( ) 1 2 1 2 ( ) = PP P B Q Q Q s t , 令 B E ( ) = ,就得到 定理 6 矩阵 A( ) 可逆的充要条件是它可以表示为一些初等矩阵的乘积。 推论 两个 s n 的 —矩阵 A( ) 与 B( ) 等价的充要条件是,有一个 s s 可逆矩阵 P( ) 与一 个 n n 可逆矩阵 Q( ) 使 B P A Q ( ) ( ) ( ) ( ) = 。 作业: P357,习题 4

预习:下一节的基本概念 §1一§3习题课 教学目标复习所学的基本概念、定理,总结学生解题时易犯的错误,通过例题与练习培养学 生运用所学概念、定理进行推理论证的能力. 教学重点:总结学生解题时易犯的错误,例题讲解 教学方法:讲授、讨论 教学过程 一、复习提问 二、作业讲评 三 例题讲解 例1P356,习题1之5) 说明:此例复习若当标准形的概念 例2.P356,习题2之2) 说明 此例复习不变因 子的概念 例3 P356,习题2之4) 说明:此例复习不变因子的概念 例4P357,习题3. 说明:此例复习不变因子的概念 四、课堂练习 练习1.P356,习题1之5) 练习2.P356,习题2之5) 作业: 预习:下一节的基本概念
预习: 下一节的基本概念. §1—§3 习题课 教学目标: 复习所学的基本概念、定理,总结学生解题时易犯的错误,通过例题与练习培养学 生运用所学概念、定理进行推理论证的能力. 教学重点: 总结学生解题时易犯的错误,例题讲解. 教学方法: 讲授、讨论 教学过程: 一、 复习提问 二、 作业讲评 三、 例题讲解 例 1 P356,习题 1 之 5) 说明: 此例复习若当标准形的概念. 例 2. P356,习题 2 之 2). 说明: 此例复习不变因子的概念. 例 3 P356,习题 2 之 4). 说明: 此例复习不变因子的概念. 例 4 P357,习题 3. 说明: 此例复习不变因子的概念. 四、课堂练习 练习 1 . P356,习题 1 之 5) 练习 2 . P356,习题 2 之 5) 作业: 预习:下一节的基本概念

§4矩阵相似的条件 教学目标掌握数字矩阵相似的充要条件。 教学重点:数字矩阵相似的充要条件。 教学方法:讲授法 教学过程 本节将给出两个n阶数字矩阵A和B相似的充要条件 引理1若有n阶数字矩阵P和Q,使 E-A=P(E-B)0, ( 则A和B相似 证明由(1)可得PQ=E,PBQ。-A,由此有Q。=R,因而A=RBP故A与B相似 引理2对任何非零n阶数字矩阵A和1一矩阵U()与V(),一定存在入一矩阵Q()与 R()及数字矩阵U,和%使 U()=(E-A)Q()+U 2 V(a)=R(a(2E-A)+% (3) 证明将U(2)改写成 U()=DA"+DA-+.+Dn+Dn 这里D,.,D都是n阶数字矩阵,而且D。≠0.若m=0,则令Q(a)=0及U。=D。,它们显然满 足引理2的要求,以下设m>0.令 0)=Q2-1+22m-2++Q.32+Q 这里Q,为待定数字矩阵.于是 (E-A002)=Q1+(Q-AQ)2-+. +(Q-AQ-)2"-+.+(Qn-1-A0n-2)1-A0.- 要使(2)式成立,只要取
§4 矩阵相似的条件 教学目标: 掌握数字矩阵相似的充要条件。 教学重点: 数字矩阵相似的充要条件。 教学方法: 讲授法. 教学过程: 本节将给出两个 n 阶数字矩阵 A 和 B 相似的充要条件. 引理 1 若有 n 阶数字矩阵 P0 和 Q0 使 0 0 E A P E B Q − = − ( ) , (1) 则 A 和 B 相似. 证明 由(1)可得 0 0 0 0 PQ E P BQ A = − , , 由此有 1 0 0 Q P , − = 因而 1 0 0 A P BP . − = 故 A 与 B 相似. 引理 2 对任何非零 n 阶数字矩阵 A 和 —矩阵 U ( ) 与 V( ) ,一定存在 —矩阵 Q( ) 与 R( ) 及数字矩阵 U0 和 V0 使 0 U E A Q U ( ) ( ) ( ) = − + (2) 0 V R E A V ( ) ( )( ) = − + (3) 证明 将 U ( ) 改写成 1 0 1 1 ( ) m m U D D D D m m − = + + + + − 这里 0 , , D D m 都是 n 阶数字矩阵,而且 0 D 0 .若 m = 0 ,则令 Q( ) 0 = 及 U D 0 0 = ,它们显然满 足引理 2 的要求,以下设 m 0. 令 1 2 0 1 2 1 ( ) . m m Q Q Q Q Q m m − − = + + + + − − 这里 Qi 为待定数字矩阵.于是 1 0 1 0 ( ) ( ) ( ) m m E A Q Q Q AQ − − = + − + 1 1 2 1 ( ) ( ) . m k Q AQ Q AQ AQ k k m m m − + − + + − − − − − − 要使(2)式成立,只要取

Q。=D,g=D+Ag,.,Q=D+Ag-.,0nm-1=Dnm1+A0.-1,U=Dnm+A0m 即可用同样的方法可求得()和。. 定理7设A,B为P上n阶方阵.则A与B相似一元E-A与1E-B等价. 证明由定理6的推论知,1E-A与E-B等价即有可逆的U()和V(2)使 AE-A=U((AE-B)V(A) 先证必要性设A=TBT,则 AE-A=AE-T-BT=T(E-B)T. 从而E-A与1E-B等价 再证充分性设有可逆的U(2)与V()使(4)成立由引理2存在Q(),R()以及数字矩阵U,和 。使(2、(3)成立,把(4)改写成 U(a)'(2E-A)=(aE-B)(, 式中的V()用(3)代入,再移项得. 「U('-(aE-B)R()]aE-A)=(aE-B)W。 上式右端等于0或是一个一次矩阵多项式,因此U(2)~-(入E-B)R(2)是一个数字矩阵,记作,即 T=U()'-(E-B)R(),T(E-A)=(2E-BW (5) 现在来证明T可逆由(5)的第一式有 E=U(A)T+U(AXE-B)R(A)=U()T+(E-AV()R(A) =[(E-BQa)+U]T+(E-A0V()R(2) =UT+(E-A)Q()T+V()R(). 等式右边第二项必须为零,否则它的次数至少是1,由于£和U,T都是数字矩阵,等式不可能成立 因此E=U。T.于是T可逆.(5)的第二式得2E-A=T~(aE-B)',再由引理1知A与B相似与 相似 矩阵A的特征矩阵入E一A的不变因子以后就简称为A的不变因子由定理即得 推论A与B相似台相似它们有相同的不变因子. 最后指出,n阶方阵A的特征矩阵E-A的秩一定是n.因此,A的不变因子总是有n个,它们
0 0 1 1 0 1 1 1 1 0 1 , , , , , , . Q D Q D AQ Q D AQ Q D AQ U D AQ = = + = + = + = + k k k m m m m m − − − − − 即可.用同样的方法可求得 R( ) 和 V0 . 定理 7 设 A , B 为 P 上 n 阶方阵.则 A 与 B 相似 − E A 与 E B− 等价. 证明 由定理 6 的推论知, E A− 与 E B− 等价即有可逆的 U ( ) 和 V( ) 使 E A U E B V − = − ( )( ) ( ) (4) 先证必要性.设 1 A T BT, − = 则 1 1 E A E T BT T E B T ( ) , − − − = − = − 从而 E A− 与 E B− 等价. 再证充分性.设有可逆的 U ( ) 与 V( ) 使(4)成立.由引理 2.存在 Q( ) ,R( ) 以及数字矩阵 U0 和 V0 使(2)、(3)成立,把(4)改写成 1 U E A E B V ( ) ( ) ( ) ( ), − − = − 式中的 V( ) 用(3)代入,再移项得. 1 0 U E B R E A E B V ( ) ( ) ( ) ( ) ( ) − − − − = − . 上式右端等于 0 或是一个一次矩阵多项式,因此 1 U E B R ( ) ( ) ( ) − − − 是一个数字矩阵,记作,即 1 0 T U E B R T E A E B V ( ) ( ) ( ), ( ) ( ) − = − − − = − (5) 现在来证明 T 可逆.由(5)的第一式有 1 E U T U E B R U T E A V R ( ) ( )( ) ( ) ( ) ( ) ( ) ( ) − = + − = + − 1 0 ( ) ( ) ( ) ( ) ( ) E B Q U T E A V R− = − + + − 1 0 U T E A Q T V R ( ) ( ) ( ) ( ) . − = + − + 等式右边第二项必须为零,否则它的次数至少是 1 ,由于 E 和 UT0 都是数字矩阵,等式不可能成立. 因此 E U T = 0 .于是 T 可逆.由(5)的第二式得 1 0 E A T E B V ( ) , − − = − .再由引理 1 知 A 与 B 相似与 相似. 矩阵 A 的特征矩阵 E A− 的不变因子以后就简称为 A 的不变因子.由定理即得 推论 A 与 B 相似 相似它们有相同的不变因子. 最后指出, n 阶方阵 A 的特征矩阵E A− 的秩一定是 n .因此, A 的不变因子总是有 n 个,它们