
第三章矩阵的初等变换与线性方程组 ·第一节矩阵的初等变换 ·第二节初等矩阵 ·第三节矩阵的秩 ·第四节线性方程组解的判别法
第三章矩阵的初等变换与线性方程组 • 第一节 矩阵的初等变换 • 第二节 初等矩阵 • 第三节 矩阵的秩 • 第四节 线性方程组解的判别法

第一节矩阵的初等变换 1、矩阵的初等变换 线性方程组的一般形式 41X1+122+.+41mXn 021火1+022火2+.+ a2nxn b2 0m11+0m2X2++0mXn=bm
第一节 矩阵的初等变换 线性方程组的一般形式 + + + = + + + = + + + = m m mn n m n n n n a x a x a x b a x a x a x b a x a x a x b 1 1 2 2 2 1 1 2 2 2 2 2 1 1 1 1 2 2 1 1 1、 矩阵的 初等变换
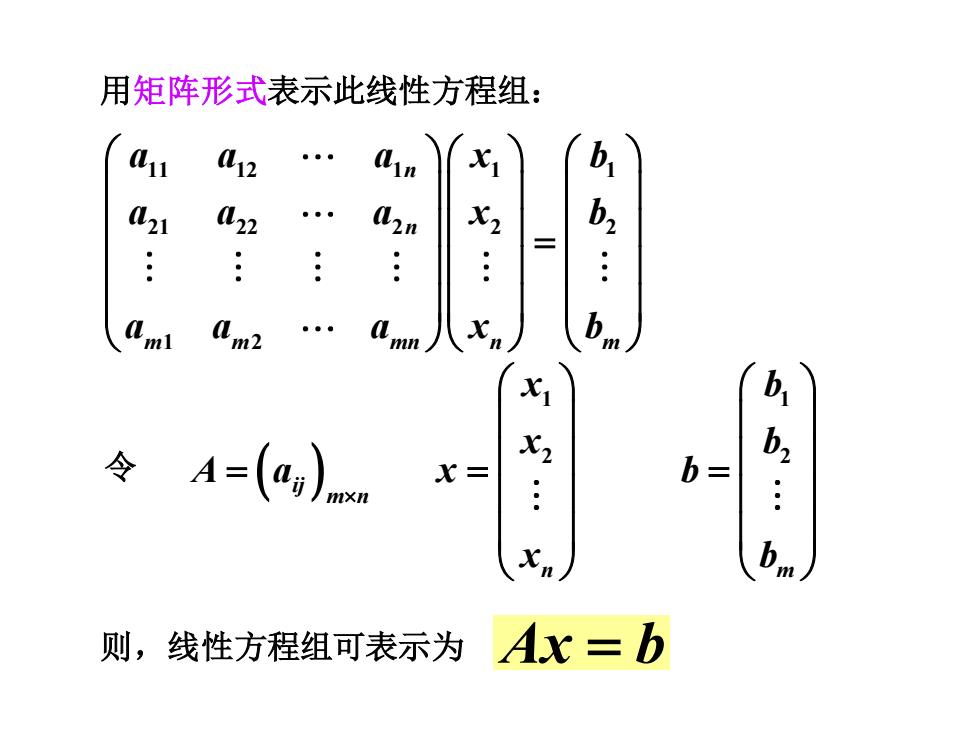
用矩阵形式表示此线性方程组: L11 12 b 21 22 02n X2 b, ● b mn 令A=(a)nn 七2 b2 X= b= Xn 则,线性方程组可表示为 Ax=b
用矩阵形式表示此线性方程组: 11 12 1 1 1 21 22 2 2 2 1 2 n n m m mn n m a a a x b a a a x b a a a x b = 令 1 2 n x x x x = 1 2 m b b b b = ( ij)m n A a = 则,线性方程组可表示为 Ax b =

如何解线性方程组?可以用消元法求解。 始终把方程组看作一个整体变形,用到如下三种变换: (1)交换方程次序; (2)以不等于0的数乘某个方程; (3)一个方程加上另一个方程的k倍. 由于三种变换都是可逆的,所以变换前的方程组与变 换后的方程组是同解的.故这三种变换是同解变换
如何解线性方程组? 可以用消元法求解。 始终把方程组看作一个整体变形,用到如下三种变换: (1)交换方程次序; (2)以不等于0的数乘某个方程; (3)一个方程加上另一个方程的k倍. 由于三种变换都是可逆的,所以变换前的方程组与变 换后的方程组是同解的.故这三种变换是同解变换.

因为在上述变换过程中,仅仅只对方程组的系数和常数 进行运算,未知量并未参与运算. 若记 l12 b B=(Ab)= l22 : ml mn 则对方程组的变换完全可以转换为 对矩阵B方程组的增广矩阵)的变换
若记 11 12 1 1 21 22 2 2 1 2 ( ) n n m m mn m a a a b a a a b B A b a a a b = = 则对方程组的变换完全可以转换为 对矩阵B(方程组的增广矩阵)的变换. 因为在上述变换过程中,仅仅只对方程组的系数和常数 进行运算,未知量并未参与运算.

即,求解线性方程组实质上是对增广矩阵施行 3种初等运算: 统称为矩阵的 (1)对调矩阵的两行。 初等行变换 (2)用非零常数k乘矩阵的某一行的所有元素。 (③)将矩阵的某一行所有元素乘以非零常数k后 加到另一行对应元素上
即,求解线性方程组实质上是对增广矩阵施行 3种初等运算: (1) 对调矩阵的两行。 (2) 用非零常数k乘矩阵的某一行的所有元素。 (3) 将矩阵的某一行所有元素乘以非零常数k后 加到另一行对应元素上。 统称为矩阵的 初等行变换

定义1:下面三种变换称为矩阵的初等行变换: (①)对调两行(对调,两行,记作→); (2)以数k≠0乘以某一行的所有元素 (3)把某一行所有元素的k倍加到另一行 对应的元素上去(第行的k倍加到第i行上 记作+k). 同理可定义矩阵的初等列变换(把“”换成 “c)
定义1:下面三种变换称为矩阵的初等行变换: (1)对调两行(对调i, j两行,记作ri rj); (2)以 数 k 0 乘以某一行的所有元素; ( ) . 3 记 作 ) 对应的元素上去(第 行 的 倍加到第 行 上 把某一行所有元素的 倍加到另一行 i krj r j k i k + 同理可定义矩阵的初等列变换 (把“r”换成 “c”).

矩阵的初等变换 「切子变焕 刀李交奂 通常称(1)对换变换(2)倍乘变换(3)倍加变换 初等变换的逆变换仍为初等变换,且变换类型相 同. 分逆变换←→ ×k逆变换方×()或片÷k +k灯逆变换5+(-k)r,或-k
矩阵的初等变换 初等列变换 初等行变换 通常称 (1) 对换变换 (2) 倍乘变换 (3) 倍加变换 初等变换的逆变换仍为初等变换, 且变换类型相 同. i j r r ri k 逆变换 ; i j r r 逆变换 ) ; 1 ( r k k ri 或 i i krj r + 逆变换 ( ) . i j i krj r + −k r 或 r −

·2、矩阵的等价 如果矩阵A经有限次初等变换变矩阵B, 就称矩阵A与B等价,记作A~B
• 2、矩阵的等价 就称矩阵 与 等价,记作 . 如果矩阵 经有限次初等变换变成矩 阵 , A B A B A B ~

等价关系的性质: ()反身性A台A; (2)对称性若A台B,则B台A; (3)传递性若A台B,B台C,则A台C. 具有上述三条性质的关系称为等价. 例如,两个线性方程组同解, 就称这两个线性方程组等价
等价关系的性质: (1) 反身性 A A; (2) 对称性 若 A B ,则 B A; (3)传递性 若 A B,B C,则 A C. 具有上述三条性质的关系称为等价. 例如,两个线性方程组同解, 就称这两个线性方程组等价