
第三章多维随机变量及其分布 9§3.1二维随变量 9§3.2边缘分布 9§3.3条件分布 9§3.4相互独立的随机变量 。§3.5两个随机变量的函数的分布
第三章 多维随机变量及其分布 §3.1 二维随机变量 §3.2 边缘分布 §3.3 条件分布 §3.4 相互独立的随机变量 §3.5 两个随机变量的函数的分布

第三章多维随机变量及其分布 9§3.1二维随机变量 9§3.2边缘分布 9§3.3条件分布 。§3.4相互独立的随机变量 9§3.5两个随机变量的函数的分布
第三章 多维随机变量及其分布 §3.1 二维随机变量 §3.2 边缘分布 §3.3 条件分布 §3.4 相互独立的随机变量 §3.5 两个随机变量的函数的分布

§3.2边缘分布 例4设二维随机变量(X,Y)的概率密度为 1 f(x,y)= 2m102V1-p exp 2(-p) -00,02>0, -1<p<1. 试求二维正态随机变的边缘概率密度
设二维随机变量(X,Y)的概率密度为 2 2 2 2 1 2 1 2 2 1 2 1 2 2 1 2 ( )( ) ( ) 2 ( ) 2(1 ) 1 exp 2 1 1 ( , ) σ y μ σ σ x μ y μ ρ σ x μ ρ σ σ ρ f x y 试求二维正态随机变量的边缘概率密度. x , y , 1 1. , , , , , 0, 0, 1 2 1 2 1 2 ρ 其 中 μ μ σ σ ρ 都是常数 且 σ σ 例4 §3.2 边缘分布

§3.2边缘分布 -1=4-2p=40=2+y- 002 解fx(x)=f(x,)d, 由于 "-[- 2 02 于是 1 fx(x)= 令=-2}
解 f (x) f (x, y)d y, X 由于 1 2 1 2 2 2 2 2 ( )( ) 2 ( ) σ σ x μ y μ ρ σ y μ , ( ) 2 1 2 2 1 2 1 1 2 2 σ x μ ρ σ x μ ρ σ y μ 于是 , 2π 1 ( ) 2 1 1 2 2 2 2 1 2 1 2(1 ) 1 2 ( ) 2 1 1 2 e e dy σ σ ρ f x σ x μ ρ σ y μ σ ρ x μ X , 1 1 1 1 2 2 2 σ x μ ρ σ y μ ρ 令 t §3.2 边缘分布 2 2 1 1 2 2 2 2 2 2 1 1 2 2 1 2 1 1 ( ) ( )( ) ( ) ( , ) exp 2 2 1 2(1 ) x μ x μ y μ y μ f x y ρ σ σ ρ ρ σ σ σ σ

§3.2边缘分布 由于-oy<o所以-0<K0,而d=Vi-p -(x-41)2 产3 、 则有fx(x) 22o7 01 1 -x-41)2 即 fx(x)= e 21 一0<X<00. V2π01 同理可得 (y-2)2 fy(y)= -e , -0<y<0. √2π02 二维正态分布的两个边缘分布都是一维正态分 布,并且都不依赖与参数p 联合分布包含更多的信息,由联合分布可以求出边 缘分布,但由边缘分布一般无法求出联合分布
则有 d , 2 1 ( ) 2 2 ( ) 1 2 2 1 2 1 e e t σ f x t σ x μ X , . 2π 1 ( ) 2 1 2 1 2 ( ) 1 e x σ f x σ x μ 即 X 同理可得 二维正态分布的两个边缘分布都是一维正态分 布,并且都不依赖与参数r , . 2 1 ( ) 2 2 2 2 2 ( ) 2 e y σ f y σ y μ Y §3.2 边缘分布 联合分布包含更多的信息,由联合分布可以求出边 缘分布,但由边缘分布一般无法求出联合分布 由于-∞<y<∞所以-∞<t<∞,而dt=dy 2 2 1 1 r

§3.2边缘分布 边缘分布均为正态分布的随机变量,其联合分 布不一定是二维正态分布,例如 令(X,)的联合密度函数为 f比,)=1。 -e 2 (1+sinxsiny), 2 显然,(X,Y)不服从正态分布但是 f()= 1-x 2e2,f0)=1e 2 √2 2π 因此边缘分布均为正态分布的随机变量,其联合分 布不一定是二维正态分布
(1 sin sin ), 2π 1 ( , ) ( , ) 2 2 2 f x y e x y X Y x y 令 的联合密度函数为 . 2 1 , ( ) 2 1 ( ) , ( , ) , 2 2 2 2 y Y x X f x e f y e X Y 显 然 不服从正态分布但 是 因此边缘分布均为正态分布的随机变量,其联合分 布不一定是二维正态分布. 边缘分布均为正态分布的随机变量,其联合分 布不一定是二维正态分布, 例如 §3.2 边缘分布

§3.2边缘分布 例设(X,Y)~f(x,y)= e',00时, fx(x)-[f(x,y)dy-Sedy=e". 当x≤0时, fx(x)=Jf(x,y)dy=0. x>0, 0, 其它
解 f x f x y y X ( ) ( , )d e y x y d f x f x y y X ( ) ( , )d . x e 当 x 0时, 0. 0, . , 0, ( ) 其 它 故 e x f x x X (1) ( ); (2) { 1} . 0, . , 0 , ( , ) ~ ( , ) f x P X Y e x y X Y f x y X y 求 其 它 例 设 当x 0时, §3.2 边缘分布

§3.2边缘分布 (2)P{X+Y≤1} =J∬fx,J)dxdy y=1-x x+y≤1 -fidf"e7dy 1/2 -f le-0-e-Jdx =1+e1-2ei
(2) P{X Y 1} x x y dx e y 1 2 1 0 d e e x x x [ ]d (1 ) 2 1 0 1 2 . 2 1 1 e e f x y x y x y ( , )d d 1 y x O x y y 1 x 1 2 §3.2 边缘分布

§3.2边缘分布 例2一整数N等可能地在1,2,3,.,10十个值中取 一个值.设D=D(N)是能整除N的正整数的个数, F=F(N)是能整除N的素数的个数试写出D和F 的联合分布律并求边缘分布律 解 样本点 12345678910 D 1223242434 F 0111121112 由此得D和F的联合分布律与边缘分布律:
解 1 2 3 4 5 6 7 8 9 10 1 2 2 3 2 4 2 4 3 4 0 1 1 1 1 2 1 1 1 2 例2 . . ( ) . . ( ) , 1,2,3, ,10 的联合分布律并求边缘分布律 是能整除 的素数的个数试写出 和 一个值 设 是能整除 的正整数的个数 一整数 等可能地在 十个值中取 F F N N D F D D N N N 由此得 D和F 的联合分布律与边缘分布律 : 样本点 D F §3.2 边缘分布
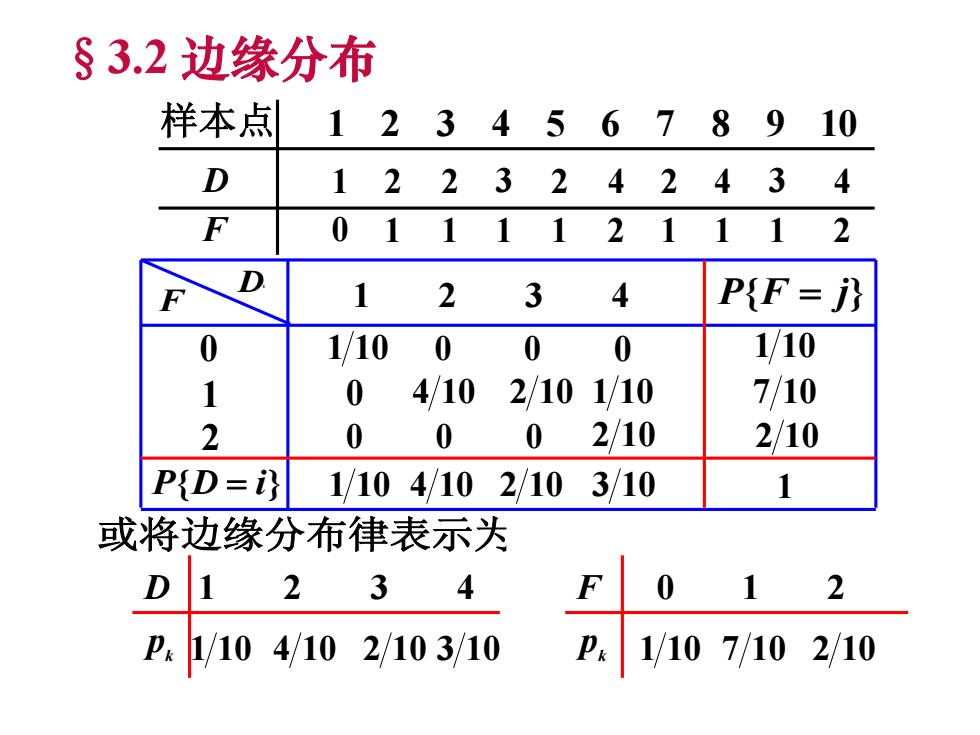
§3.2边缘分布 样本点 12 345678910 D 1223242434 F 01 11121112 D 23 4 P{F=} 0 1/10 0 0 0 1/10 1 04/10 2/101/10 7/10 2 0 0 0 2/10 2/10 P{D=} 1/104/102/103/10 1 或将边缘分布律表示为 23 4 F 2 P.1/104/102/103/10 P.1/107/102/10
D k p 1 2 3 4 1 10 4 10 2 10 3 10 F k p 0 1 2 1 10 7 10 2 10 1 2 3 4 1 10 0 0 0 0 4 10 2 10 1 10 0 0 0 2 10 D F P{F j} 1 10 7 10 2 10 P{D i} 1 10 4 10 2 10 3 10 1 或将边缘分布律表示为 1 2 3 4 5 6 7 8 9 10 1 2 2 3 2 4 2 4 3 4 0 1 1 1 1 2 1 1 1 2 样本点 D F 0 1 2 §3.2 边缘分布