
第五章 矩阵的特征值与特征向量 一.向量的正交及正交矩阵 二.方阵的特征值与特征向量 三.相似矩阵 四.实对称矩阵的对角化
第五章 矩阵的特征值与特征向量 一.向量的正交及正交矩阵 二.方阵的特征值与特征向量 三. 相似矩阵 四. 实对称矩阵的对角化
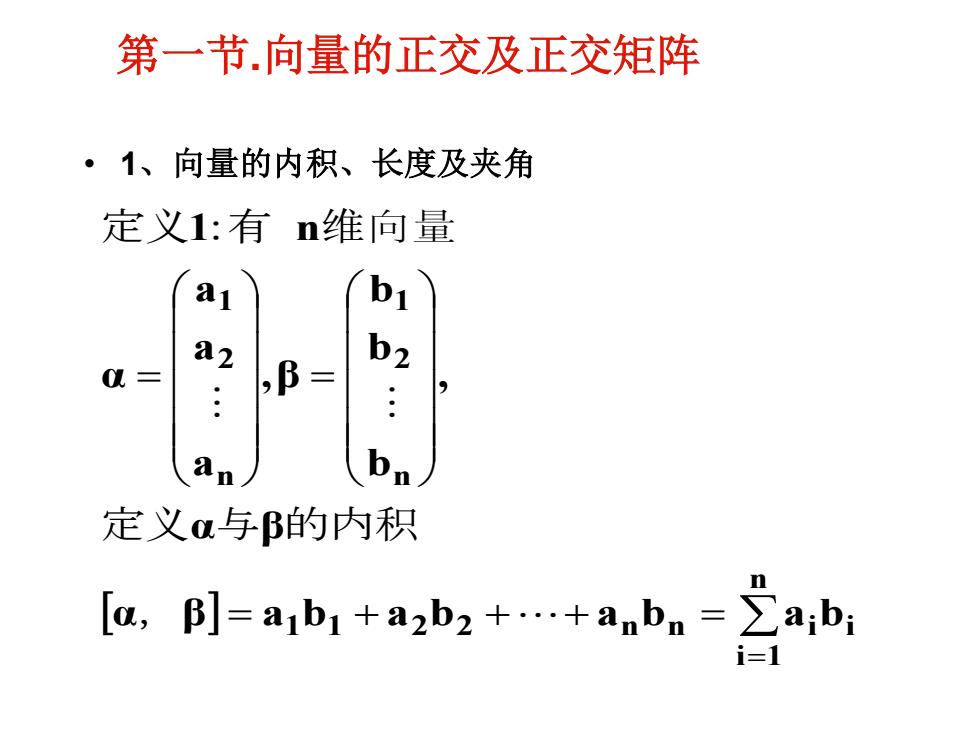
第一节向量的正交及正交矩阵 ·1、向量的内积、长度及夹角 定义1:有n维向量 a1 82 b2 0L= ,B= bn 定义α与的内积 [a,]=a1b1+azb2+.+anbn=∑abi i=1
• 1、向量的内积、长度及夹角 第一节.向量的正交及正交矩阵 = = + + + = = = n i 1 1 1 2 2 n n i i n 2 1 n 2 1 α β a b a b a b a b α β , b b b ,β a a a α 1 n , 定义 与 的内积 定义 :有 维向量

[a,B]=a"B=B"a 向量的内积具有下列性质 1、[α,]≥0当且仅且a=0时,等号成立 2[a,]=B,a] 3[a,B+Y]=[a,]+[a,y] 4、[a,]=[.a,]=[a,p] 其中a,B,y为n维向量,)为实数;
T T , = = 其中 , , 为 维向量, 为实数; 、 , , , 、 , , , ; 、 , , ; 、 , 当且仅且 时,等号成立; 向量的内积 α β γ n λ 4 λ α β λα β α λβ 3 α β γ α β α γ 2 α β β α 1 α α 0 α 0 = = + = + = = 具有下列性质

定义2:规定向量aw=(a1,a2,.an) 的模(或长度) la=Ma,a]=vap+a+.+a 若=1,则称为单位向量;
( ) 若 ,则称 为单位向量; , 的模(或长度) 定义 :规定向量 1 , , 2 2 2 2 1 1 2 = = = + + + = n T n a a a a a a 2

向量的长度具有以下性质 1、非负性,当a≠0时,0; 当a=0时,=0; 2、齐次性,=2l; 3、施瓦兹不等式[a,]≤: 4三角不等式a+≤a+P
4 α β α β 3 α β α β 2 λα λ α α 0 α 0 1 α 0 α 0 + + = = = 、三角不等式 、 不等式 , ; 、 次性, ; 当 时, ; 、 性,当 时, 〉 ; 向量的 具有以下性质 施瓦兹 齐 非负 长度

定义3规定n维非零向量 41 0 b2 & 6B= .: 的夹角为 an bn 9=arccos,月s1I a Bl
定义3规定n维非零向量 = = n bn b b a a a 2 1 2 1 , 的夹角为 1 , = arccos

单位向量 x 00
单位向量 0 =

2、向量的正交性 定义4:若n维向量 与β的内积a,B=0,则称a与阝 正交。 称两两正交的n维非零向量组为正 交向量组
2、向量的正交性 定义4:若n维向量 正交。 与的内积, = 0,则称与 称两两正交的n维非零向量组为正 交向量组

定理3:n维向量组0y1,02,“,C是一组两两正交的非零向 量,则041,02,0线性无关。 证明: 设有2,2.几,使 1必1+202+.+,=0 以a左乘上式两端,得到 a1=0,因为a1≠0, a41=a12≠0
n维向量组 是一组两两正交的非零向 量,则 线性无关。 r , , , 定理3: 1 2 r , , , 1 2 证明: 0 0 0 2 1 1 1 1 1 1 1 1 1 2 2 1 2 = = + + + = T r r r 因为 , 以 左乘上式两端,得到 设有 , , 使 0 , 1 T T

从而必有=0。类似可以证明 2=.=2=0,于是,Q1,a2.0 线性无关
r r 2 1 2 1 0, 0 于是, , 从而必有 。类似可以证明 = = = = 线性无关