
第二章随机变量及其分布 6§2.1随机变量 。§2.2离散型随机变量及其概率分布 9§2.3随机变量的分布函数 9§2.4连续型随机变量及其概室密度 §2.5随机变量的函数的分布 2142
第二章 随机变量及其分布 §2.1 随机变量 §2.2 离散型随机变量及其概率分布 §2.3 随机变量的分布函数 §2.4 连续型随机变量及其概率密度 §2.5 随机变量的函数的分布 2/42

§2.4连续型随机变量及其概率密度 连续型随机变量及概率密度定义: 。如果对于随机变量X的分布函数Fx),存在非负可积函 数x),使对于任意实数x有 F)=[f(dr 则称X为连续型随机变量,其中函数x)称为X的概率密 度函数,简称概率密度 。※由数学分析的知识,连续型随机 儿种提法: 变量的分布函数是连续函数 X的概率分布: 是指分布函数 ·必在实际应用中遇到的基本上是 X为连续型时: 离散和连续型随机变量 是指概率密度 X为离散型时: 是指分布律
§2.4 连续型随机变量及其概率密度 连续型随机变量及概率密度 定义: 如果对于随机变量X的分布函数F(x),存在非负可积函 数f(x),使对于任意实数x有 F(x)= 则称X为连续型随机变量,其中函数f(x)称为X的概率密 度函数,简称概率密度 ※由数学分析的知识,连续型随机 变量的分布函数是连续函数 ※在实际应用中遇到的基本上是 离散和连续型随机变量 x f t dt - ( ) 几种提法: X的概率分布: 是指分布函数 X为连续型时: 是指概率密度 X为离散型时: 是指分布律
§2.4连续型随机变量及其概率密度 9概率密度函数的性质: 。1°非负性:fx)≥0.由定义可知 。2°规范性:f(x)d=F(o)=1 曲线y=x)与Ox轴之间的面积等于1 ●3°对任意实数x1,x2≤2),有Px<X≤2}=Fc2)一Fc1) f(x)ds ·概率Px<X≤x2}等于区间c12l上曲线y=x)之下曲边梯形的面积 ●4°若fx)在点x处连续,则有Fx)=fx) Ax) ·比右连续强,一般的是右连续) X1 X2
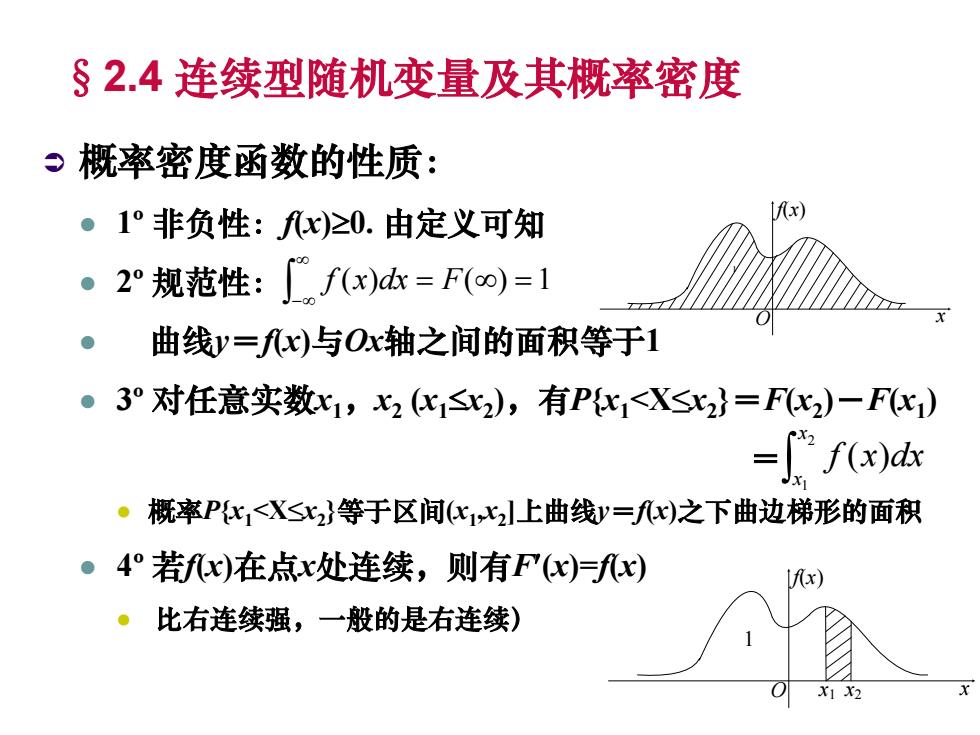
§2.4 连续型随机变量及其概率密度 概率密度函数的性质: 1º 非负性:f(x)0. 由定义可知 2º 规范性: 曲线y=f(x)与Ox轴之间的面积等于1 3º 对任意实数x1,x2 (x1x2 ),有P{x1<X≤x2 }=F(x2 )-F(x1 ) = 概率P{x1<X≤x2 }等于区间(x1 ,x2 ]上曲线y=f(x)之下曲边梯形的面积 4º 若f(x)在点x处连续,则有F(x)=f(x) 比右连续强,一般的是右连续) f (x)dx F() 1 1 O x f(x) 1 O x f(x) x1 x2 2 1 ( ) x x f x dx

§2.4连续型随机变量及其概率密度 pa)一维随机变量的概率密度的线密度含义: 由连续性定义,在连续点处有 F(x+△x)-F(x) P{x<X<x+△ ●fx)=lim =lim △r→0+ △x △x0+ △x 。这正好与物理学中的线密度的定义类似:随机点落在单 位区间上概率的大小 ·当△x充分小时,点x处的曲边梯形可近似为长△x高fx) 的矩形。 即Px<X≤x+△x}≈fx)△x,随机变量X落在c,x+△x 的概率近似等于x)△x,忽略了高阶无穷小。 5
§2.4 连续型随机变量及其概率密度 a) 一维随机变量的概率密度的线密度含义: 由连续性定义,在连续点x处有 f(x)= = 这正好与物理学中的线密度的定义类似:随机点落在单 位区间上概率的大小 当∆x充分小时,点x处的曲边梯形可近似为长∆x高f(x) 的矩形。 即P{x<X≤x+∆x }≈f(x)∆x,随机变量X落在(x,x+∆x] 的概率近似等于f(x)∆x,忽略了高阶无穷小。 x F x x F x x ( ) ( ) lim 0 x P x X x x x { } lim 0 5

§2.4连续型随机变量及其概率密度 9b)对于连续型随机变量,单点概率为0 ·即若X为连续型随机变量,对任意的实数a,有PX=u}=0 p证:显然有包含关系{X=c{a一△r<X≤M} o.'.0sP{X=a}≤P{a一△x<X≤M}=F(a一F(a-△x) ● 而Fx)是连续的(也满足左连续),因为连续型随机变量的分布函 数是连续的 。∴.当△x→0时有0≤P{X=sIim(F(a-△)-F(a)=F(a)-F(a)=0 1 。即P{X=}=0 P(A)=0不能→A=Φ 要注意几点: P(A)=1不能→A=S 。1°只有当X为连续型时,才一定有P{公==0,则不一定 ● 2°尽管P=}=0,但{X=}不是不可能事件 3°连续型随机变量中区间的端点不影响概率值,即对以下概率 不加区分P{<X≤b}=P{asX≤b}=P{sX<b}=P{a<X<b} 6
§2.4 连续型随机变量及其概率密度 b) 对于连续型随机变量,单点概率为0 即若X为连续型随机变量,对任意的实数a,有P{X=a }=0 证:显然有包含关系{X=a}{a-∆x<X≤a } ∴0≤P{X=a }≤P{a-∆x<X≤a }=F(a)-F(a-∆x) 而F(x)是连续的(也满足左连续),因为连续型随机变量的分布函 数是连续的 ∴当∆x→0时有0P{X=a}≤ 即P{X=a}=0 要注意几点: 1°只有当X为连续型时,才一定有P{X=a}=0,否则不一定 2°尽管P{X=a}=0,但{X=a }不是不可能事件 3°连续型随机变量中区间的端点不影响概率值,即对以下概率 不加区分 P{a<X≤b}=P{a≤X≤b}=P{a≤X<b}=P{a<X<b} lim( ( ) ( )) ( ) ( ) 0 0 F a x F a F a F a x 6 P(A)=0不能 A=Φ P(A)=1不能 A=S

§2.4连续型随机变量及其概率密度 例:由分布函数求概率密度 0, x<1 设F(x)= lnx,1≤x<e,求fx) 1, x≥e 。解:先判断Fx)在区间端点的连续性(是否有阶跃特性), 如果连续则直接对Fx)进行分段求导即可,由于连续型 随机变量单点概率为0,不可导的点可直接取右导数即 可,也可随意给定。 0, x<1 f(x)= dF(x) /1 1/x,1≤x<e 1≤x<e= dx 0, 其它 0, x≥e 7
§2.4 连续型随机变量及其概率密度 例:由分布函数求概率密度 设 ,求f(x) 解:先判断F(x)在区间端点的连续性(是否有阶跃特性), 如果连续则直接对F(x)进行分段求导即可,由于连续型 随机变量单点概率为0,不可导的点可直接取右导数即 可,也可随意给定。 x e x x e x F x 1, ln , 1 0, 1 ( ) 0, 其它 1/ , 1 0, , 1 1 0, 1 ( ) ( ) x x e x e x e x x dx dF x f x 7

§2.4连续型随机变量及其概率密度 例1:由概率密度求分布函数和概率 kx, 0≤x<3 ·设随机变量X具有概率密度f(x)=2- X 3≤x≤4 0, 其它 。(1)确定常数k;(2)求Fx);(3)求P{1<X≤7/2} 解:()由规范性得1xd+(2-x/2)k,解得k=1/6; ·(2)由定义 0, x<0 0 x<0 x/6dx, 0≤x<3 0≤x<3 oF)=∫.f0dt= x2/12, */+(2-x/234 -3+2x-x2/4,3≤x<4 x≥4 1, x≥4 ●(3)P{1<X≤7/2}=F(7/2)-F1)=41/48 ●或者用性质(3)在区间(1,7/21上对fx)积分 8
§2.4 连续型随机变量及其概率密度 例1:由概率密度求分布函数和概率 设随机变量X具有概率密度 (1)确定常数k;(2)求F(x);(3)求P{1<X≤7/2 } 解: (1) 由规范性得 1= ,解得k=1/6; (2) 由定义 (3) P{1<X≤7/2 }=F(7/2)-F(1)=41/48 或者用性质(3)在区间(1,7/2]上对f(x)积分 0, 其它 , 3 4 2 2 , 0 3 ( ) x x k x x f x 4 3 3 0 kxdx (2 x / 2)dx 1, 4 3 2 / 4 ,3 4 /12, 0 3 0, 0 1, 4 / 6 (2 / 2) ,3 4 / 6 , 0 3 0, 0 ( ) ( ) 2 2 3 3 0 0 x x x x x x x x x dx x dx x x dx x x F x f t dt x x x - 8

§2.4连续型随机变量及其概率密度 。三种重要的连续型随机变量 (一)均匀分布 Lfx) ·设连续型随机变量X具有概率密度 1 1 b-a f(x)=3b-a ,a<x<b 0, 其它 ●则称x在区间(a,b)上服从均匀分布.记为X~U(a,b)。 。例如:电子和量子在一定能级上的运动轨迹 数值计算中,研究四舍五入引起的误差。 概室密度的两个条件显然成立: 。 非负性成立fx)≥0,且规范性:f)dh=1 9
§2.4 连续型随机变量及其概率密度 三种重要的连续型随机变量 (一)均匀分布 设连续型随机变量X具有概率密度 则称x在区间(a,b)上服从均匀分布.记为X~U(a,b)。 例如:电子和量子在一定能级上的运动轨迹 数值计算中,研究四舍五入引起的误差。 概率密度的两个条件显然成立: 非负性成立f(x)0,且规范性: =1 0, 其它 , 1 ( ) a x b f x b a - f (t)dt O x f(x) a b b a 1 9
§2.4连续型随机变量及其概率密度 9X的分布函数: F(x) x<a 1 F(x)=∫fodh= ,a≤x<b b-a 1. x≥b Fx)为fx)的积分图像 。关于自变量范围:连续型随机变量概率密度函数的自变量一定是 在(一∞,∞)上都有定义,有些区间函数值为0,表明随机变量X落在 这些区间的概率为0,或不可能事件。 。均匀分布的含义:代表一种等可能性,即X落在区间(a,b)中任意等 长度的子区间内的概率是等可能的,或者说X落在区间(α,b)中的概 率只依赖于子区间长度而与子区间位置无关。 9证:对任意长度为的子区间(c,c+),≤c<c+b,有 。Pte<Xe+n="h-6'aaa -a 几何概型 10
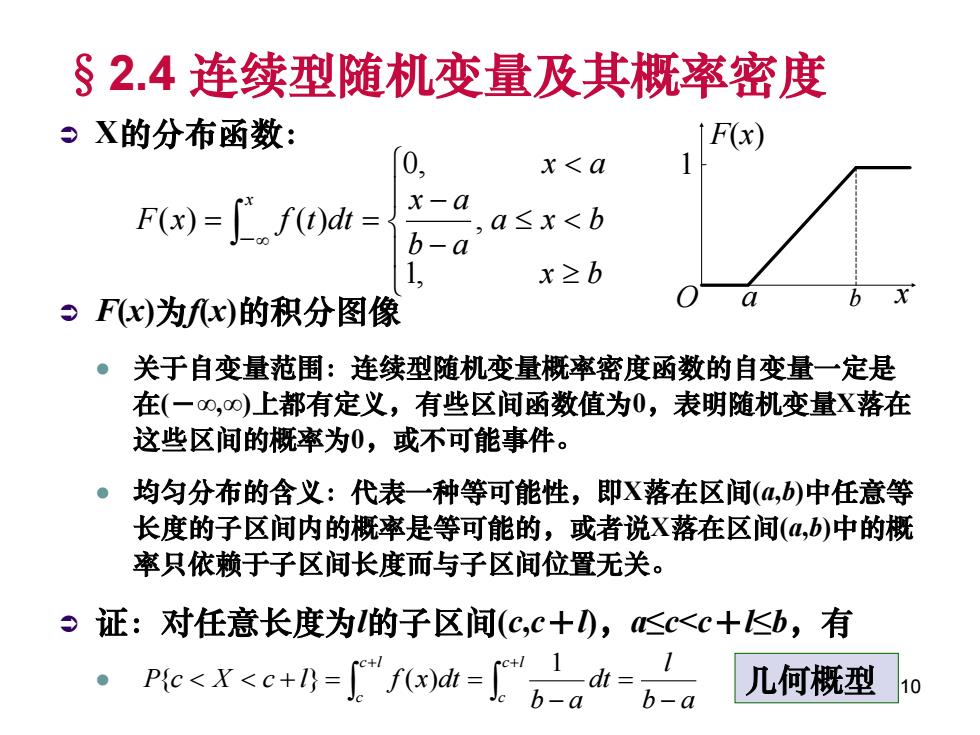
§2.4 连续型随机变量及其概率密度 X的分布函数: F(x)为f(x)的积分图像 关于自变量范围:连续型随机变量概率密度函数的自变量一定是 在(-∞,∞)上都有定义,有些区间函数值为0,表明随机变量X落在 这些区间的概率为0,或不可能事件。 均匀分布的含义:代表一种等可能性,即X落在区间(a,b)中任意等 长度的子区间内的概率是等可能的,或者说X落在区间(a,b)中的概 率只依赖于子区间长度而与子区间位置无关。 证:对任意长度为l的子区间(c,c+l),a≤c<c+l≤b,有 x b a x b b a x a x a F x f t dt x 1, , 0, ( ) ( ) - b a l dt b a P c X c l f x dt c l c c l c 1 { } ( ) O x F(x) a b 1 几何概型 10

§2.4连续型随机变量及其概率密度 例2:设电阻值R是一个随机变量,均匀分布在 9002~11002。求R的概率密度及R落在9502~ 10502的概率。X~U(900,1100) 9解:首先由题意均匀分布,得到R的概率密度函 数为 f(x)=1100-900 900<r<1100 0, 其它 p1050] ∴.P950<R≤1050}= t=0.5 J950200 11
§2.4 连续型随机变量及其概率密度 例2: 设电阻值R是一个随机变量,均匀分布在 900Ω~1100Ω。求R的概率密度及R落在950Ω~ 1050Ω的概率。X~U(900,1100) 解:首先由题意均匀分布,得到R的概率密度函 数为 ∴P{950<R≤1050}= =0.5 0, 其它 , 900 1100 1100 900 1 ( ) r f x 1050 950 200 1 dt 11