
第四章向量组的线性相关性 一.向量组及其线性组合 二.向量组的线性相关性 三.向量组的秩 四。向量空间 五.线性方程组解的结构
二. 向量组的线性相关性 一. 向量组及其线性组合 三. 向量组的秩 第四章 向量组的线性相关性 四. 向量空间 五. 线性方程组解的结构

第一节:向量组及其线性组合 1.向量的定义及其运算 定义:n个有次序的数1,42,.,4m所组成的有序数组 (1,2,.,4n)称为一个n维向量。 这n个数称为该向量的n个分量,第i个数: 称为第i个分量。 分量全为实数的向量称为实向量, 分量全为复数的向量称为复向量 以后我们用小写希腊字母,B,Y.来代表向量
第一节:向量组及其线性组合 分量全为复数的向量称为复向量. 分量全为实数的向量称为实向量, 1. 向量的定义及其运算 定义:n 个有次序的数 1 2 , , , n a a a 所组成的有序数组 ( ) 1 2 , , , n a a a 称为一个n 维向量。 这 n 个数称为该向量的n 个分量,第 个数 称为第 个分量。 i i i a 以后我们用小写希腊字母 , , 来代表向量
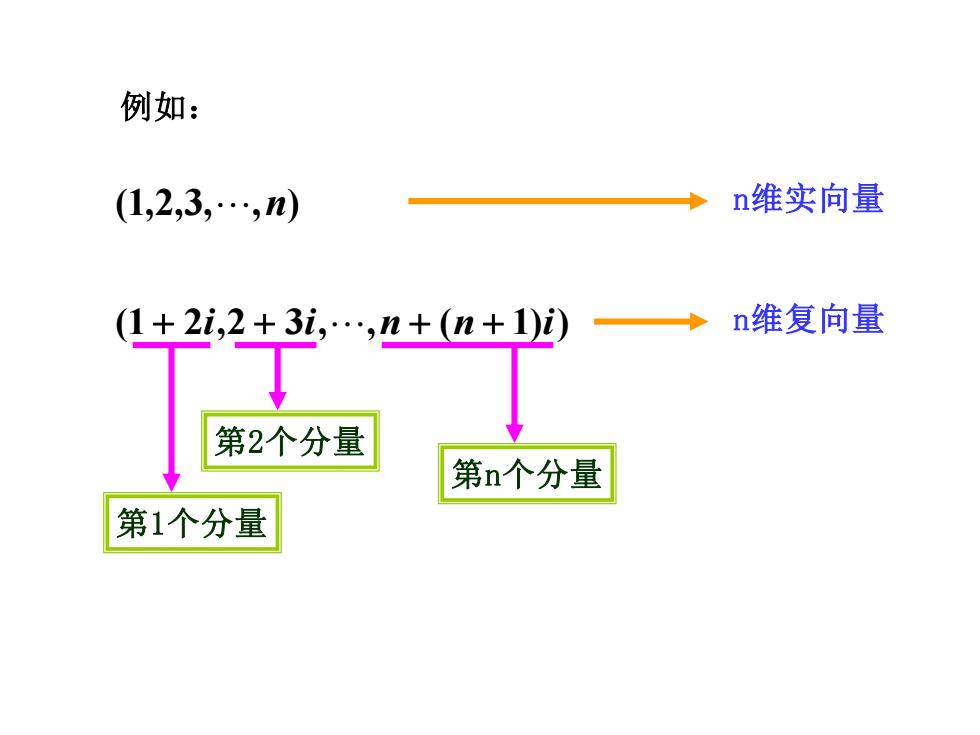
例如: (1,2,3,.,m) n维实向量 (1+2i,2+3i,.,n+(n+1)i)→ n维复向量 第2个分量 第n个分量 第1个分量
例如: (1,2,3, ,n) (1 + 2i,2 + 3i, ,n + (n + 1)i) n维实向量 n维复向量 第1个分量 第n个分量 第2个分量

向量通常写成一行:&=(41,42,.,4n) 称为行向量。 a 有时也写成一列: 0= 称为列向量。 它们的区别 只是写法上 a, 的不同。 分量全为零的向量(0,0,.,0) 称为零向量。 2.向量的运算和性质 向量相等:如果n维向量=(a1,42,.,4n) B=(b1,b2,.,bn) 的对应分量都相等,即4=b(i=1,2,n) 就称这两个向量相等,记为=B
向量通常写成一行: ( ) 1 2 , , , n = a a a 有时也写成一列: 1 2 n a a a = 称为行向量。 称为列向量。 它们的区别 只是写法上 的不同。 分量全为零的向量 (0,0, ,0) 称为零向量。 2. 向量的运算和性质 向量相等:如果n 维向量 ( ) 1 2 , , , n = a a a ( ) 1 2 , , , n = b b b 的对应分量都相等,即 1,2, , ( ) i i a b i n = = 就称这两个向量相等,记为 =

向量加法:向量Y=(a1+b,42+b2,.,4n+bn) 称为向量a=(41,42,.,m B=(b1,b2,.,bn) 的和,记为y=a+B 负向量:向量x=(-41,一4,.,一0n)称为向量a的负向量 向量减法:a-B=a+(-B) 数乘向量:设k为数域p中的数,向量(k1,ka2,.,kan) 称为向量a=(a1,42,.,4n) 与数k的数量乘积。记为k0
向量加法:向量 ( ) 1 1 2 2 , , , n n = + + + a b a b a b 称为向量 ( ) 1 2 , , , n = a a a ( ) 1 2 , , , n = b b b 的和,记为 = + 负向量:向量 ( ) 1 2 , , , n = − − − a a a 称为向量 的负向量 向量减法: − = + −( ) 数乘向量:设k为数域p中的数,向量 ( ) 1 2 , , , n ka ka ka 称为向量 ( ) 1 2 , , , n = a a a 与数k的数量乘积。记为 k

满足运算律: (1)a+B=B+a (5)1·a=a (2)(a+B)+y=(a+B)+Y(6)k(lc)=(kl)a (3)a+0=a (7)k+1)a=ka+la (4)a+(-a)=0 (8)k(a+B)=ka+kB 注:(1)对任意的向量心,存在唯一的零向量0, 使得a+0=a (2) 对任意的向量a,存在唯一的负向量-a, 使得a+(-)=0 (3)0a=0;(-1)a=-;20=0. (4)如果2=0,则2=0或a=0
(4) ( ) 0 (3) 0 (2)( ) ( ) (1) + − = + = + + = + + + = + ( ) ( ) k k k k l k l k l kl + = + + = + = = (8) (7) (6) ( ) ( ) (5)1 满足运算律: 注:(1)对任意的向量 , 存在唯一的零向量 o, 使得 + = o (2)对任意的向量 , 存在唯一的负向量 −, 使得 + − = ( ) o (4)如果 = 0, 则 = = 0 0 或 (3) 0 0; ( 1) ; 0 0. = − = − =

2.向量的线性组合 定义1:给定向量组A:a1,02,Cm’ 对于任何一组实数k1,k2,.,km, 向量kC1+k22+.+kmCm称为向量组A的一个 线性组合,k1,k2,.,km称为这个线性组合的系数。 定义2:给定向量组A:01,2,.,Qm,和向量B 如果存在一组实数入1,入2,.九m, 使得B=几必1+人2a2+.+九mCm 则称向量B是向量组A的线性组合, 或称向量B能由向量组A线性表示
2. 向量的 线性组合 定义1:给定向量组 1 2 : , , , , A m 对于任何一组实数 1 2 , , , , m k k k 向量 1 1 2 2 m m k k k + + + 称为向量组A的一个 线性组合, 1 2 , , , m k k k 称为这个线性组合的系数。 定义2:给定向量组 1 2 : , , , , A m 和向量 如果存在一组实数 1 2 , , , m 使得 = + + + 1 1 2 2 m m 则称向量 是向量组A的线性组合, 或称向量 能由向量组A线性表示。
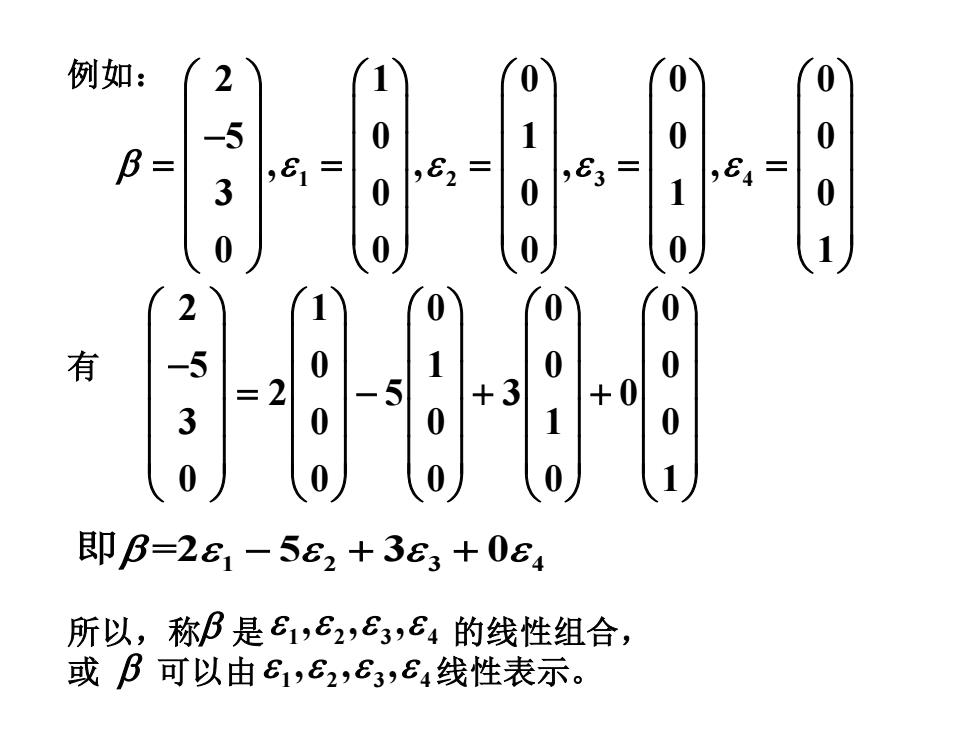
例如: 2 1 0 0 0 -5 0 0 B= 3 0 ,82= 0 ,63= 1 )84= 0 0 0 0 0 2 0 0 0 有 -5 0 1 0 0 =2 0 -5 +3 +0 3 0 1 0 0 0 0 1 即B=281-582+363+084 所以,称B是61,82,83,B4的线性组合, 或B可以由E1,E2,83,84线性表示
例如: 1 2 3 4 2 1 0 0 0 5 0 1 0 0 , , , , 3 0 0 1 0 0 0 0 0 1 − = = = = = 有 2 1 0 0 0 5 0 1 0 0 2 5 3 0 3 0 0 1 0 0 0 0 0 1 − = − + + 即 =2 5 3 0 1 2 3 4 − + + 所以,称 是 的线性组合, 或 可以由 线性表示。 1 2 3 4 , 1 2 3 4

判断向量B可否由向量组01,02,.,0m线性表示的定理。 定理1:向量B可由向量组c1,c2,.,Qm线性表示的 充分必要条件是: 以01,02,.,Cm为系数列向量,以B为常数项列向量 的线性方程组有解,且一个解就是线性表示的系数。 线性方程组的矩阵表示和向量表示: 011x1+ 012X2+ 十 ainXn 三 b L21X1 十 L22X2 十. a2nXn b2 0m1x1+ m22++mn
定理1: 判断向量 可否由向量组 1 2 , , , m 线性表示的定理。 向量 可由向量组 线性表示的 充分必要条件是: 1 2 , , , m 以 1 2 , , , m 为系数列向量,以 为常数项列向量 的线性方程组有解,且一个解就是线性表示的系数。 线性方程组的矩阵表示和向量表示: + + + = + + + = + + + = m m mn n m n n n n a x a x a x b a x a x a x b a x a x a x b 1 1 2 2 2 1 1 2 2 2 2 2 1 1 1 1 2 2 1 1

12 L21 L22 A= X= b= m2 n 方程组可表示为x=b 若A=(a,c2,an) 则方程组的向量表示为XC1+x22+.+xnCn=b
令 11 12 1 21 22 2 1 2 n n m m mn a a a a a a A a a a = 1 1 2 2 n m x b x b x b x b = = 方程组可表示为 Ax b = ( ) 1 2 , , , 若A = n 则方程组的向量表示为 1 1 2 2 n n x x x b + + + =