
《线性代数》教学大纲 Linearity Algebra 适用专业:适用网络工程专业 课程学时:40学时 课程学分:2学分 课程代码: 先修课程:高等数学 一、课程的性质和任务 《线性代数》是工科院校学生的 一门必多基础课,是学习自然科学、工程技术和企业管理所必 备的基础知识和重要工具。学习本课程的目的,是使学生获得行列式、矩阵代数、线性方程组,线性 掌握基本运算,培养逻辑思维、逻辑推理和运用矩阵代数解决某些实际 的火要的基 判 线性 数不仅是物理 电 二、课程教学的基本要求及基本内容 1、理解下列基本概念 n阶行列式 mXn矩阵 矩阵的秩及初等变换 初等矩阵 n维向量组 的线性相关及线性无关 向量的线性组合 向量组的极大无关组与秩 n维向 量空间齐次线性方程组的基础解系 齐次与非齐次线性方程组的通解 佰阵的结 征值与特征向量 相似矩阵与相似 矩 车 交变换 二次型及标 准形 合同变换与合同矩阵 二次型和对应矩阵的正定性 2、掌握下列基本运算 行列式的计算方法 矩连的计管 逆矩连的求法 线性方程组的解 法 矩阵的特征值和特征向量的求法 用正交变换化二次型为标准形 3、培养逻辑思维、逻辑推理和运用矩阵代数解决某些实际问题的能力,为学习后继课程和工作打下 必要的 基本内容: 第一章:行列式 本章教学重点:行列式是一种常用的数学工具,在数学及其它学科中有着广泛的应用。让 学生了解行列式的性质及了解线性方程组的克莱姆法则,掌握行列式的常用计算方法 本章教学难点:学生了解行列式的性质及了解线性方程组的克莱姆法则,掌握行列式的常 用计算方法 教学内容: 第一节 二阶与三阶行列式1、二阶行列式 2、三阶行列式 第二节 n阶行列式的定义。1、排列与逆序2、n阶行列式的定义3、对换 第三节 行列式的性质 第四节 行列式的展开与计算 1、余子式与代数余子式 2、行列式的展开定理 3、行列式的计算 第五节克莱姆法则 第二章:矩阵及其运算
《线性代数》教学大纲 Linearity Algebra 适用专业:适用网络工程专业 课程学时:40学时 课程学分:2学分 课程代码: 先修课程:高等数学 一、课程的性质和任务 《线性代数》是工科院校学生的一门必修基础课,是学习自然科学、工程技术和企业管理所必 备的基础知识和重要工具。学习本课程的目的,是使学生获得行列式、矩阵代数、线性方程组,线性 变换及二次型等基本知识,掌握基本运算,培养逻辑思维、逻辑推理和运用矩阵代数解决某些实际 问题的能力,为学习后继课程和工作打下必要的基础知识。线性代数不仅是物理、力学、电路、运 筹等课程的理论基础,而且随着计算机的飞速发展和广泛应用,使许多实际问题可以通过离散化的 数值计算得到定量解决,这样,作为处理离散问题的线性代数成为大学生今后从事科学研究和工程 设计必备的数学基础。 二、课程教学的基本要求及基本内容 1、理解下列基本概念 n阶行列式 m×n矩阵 矩阵的秩及初等变换 初等矩阵 n维向量组 的线性相关及线性无关 向量的线性组合 向量组的极大无关组与秩 n维向 量空间齐次线性方程组的基础解系 齐次与非齐次线性方程组的通解 矩阵的特 征值与特征向量 相似矩阵与相似变换 正交矩阵与正交变换 二次型及标 准形 合同变换与合同矩阵 二次型和对应矩阵的正定性 2、掌握下列基本运算 行列式的计算方法 矩阵的计算 逆矩阵的求法 线性方程组的解 法 矩阵的特征值和特征向量的求法 用正交变换化二次型为标准形 3、培养逻辑思维、逻辑推理和运用矩阵代数解决某些实际问题的能力,为学习后继课程和工作打下 必要的 基本内容: 第一章 :行列式 本章教学重点:行列式是一种常用的数学工具,在数学及其它学科中有着广泛的应用。让 学生了解行列式的性质及了解线性方程组的克莱姆法则,掌握行列式的常用计算方法 本章教学难点:学生了解行列式的性质及了解线性方程组的克莱姆法则,掌握行列式的常 用计算方法 教学内容: 第一节 二阶与三阶行列式 1、二阶行列式 2、三阶行列式 第二节 n阶行列式的定义。1、排列与逆序 2、n阶行列式的定义 3、对换 第三节 行列式的性质 第四节 行列式的展开与计算 1、余子式与代数余子式 2、行列式的展开定理 3、行列式的计算 第五节 克莱姆法则 第二章:矩阵及其运算

本章教学重点:矩阵是线性代数的主要研究对象。它在线性代数与数学的许多分支中都有 重要应用,许多实际问题可用矩阵表示并用有关理论得到解决。本节让学生掌握矩阵的运 算规律及求逆矩阵的方法,要让学生了解矩阵常用的分块方法 本章教学难点:在于让学生掌握矩阵的运算规律及求逆矩阵的方法,要让学生了解矩阵常 用的分块方法。 教学内容: 第一节 矩阵 1、矩阵 2、矩阵的相等3、几个常用的特殊矩阵 第二节 矩阵的运算 1、矩连的加法 2、数与矩阵相乘 3、矩阵与矩阵相乘 4、矩阵的转置 5、方阵的行列式 第三节逆矩阵 1、逆矩阵的概念 2、前矩连的性质3、方连的可㎡条件与逆矩年的十得 第四节分块矩阵 1、分块矩阵 2、分块对角阵 第三章:矩阵的初等变换与线性方程组 本章教学重点:矩阵的初等变换是矩阵的 一种重要运算。让学生掌握用矩阵的初等行变换 求矩阵的秩、求逆矩阵、解线性方程组的方法,要让学生了解初等矩阵的作用。 本章教学难点:让学生掌握用矩阵的初等行变换求矩阵的秩、求逆矩阵、解线性方程组的 方法,要让学牛了解初等矩阵的作用。 教学内容: 第一节 矩阵的初等变换1、矩阵的初等变换 2、矩阵等价3、矩阵的标准型 第二节 初等矩阵1、初等矩阵 2、利用初等变换求逆矩阵 第三节 矩阵的秩1、矩阵的秩 2、利用初等变换求矩阵的秩3、矩阵秩的性质 第四节 线性方程组解的判别法 第四章:向量组的线性相关性 本章教学重点:向量组的线性相关与线性无关是线性代数的重要内容,在此基础上可讨论 线性方程组的通解问题。】 掌握向量组的线性相关与线性 天的 定义及有关的性质, 掌握齐次线性方程组的基础解系和通解的求法,理解非齐次线性方程组解的结构及通解的 概念。 本章教学难点:让学生掌握向量组的线性相关与线性无关的定义及有关的性质,掌握齐次 线性方程组的基础解系和通解的求法, 理解非齐次线性方程组解的结构及通解的概念。 教学内容: 第一节向量组及其线性组合 1、向量的定义及其运算2、向量的线性组合3、向量组的线性表示 第二节向量组的线性相关性 1、线性相关与线性无关2、向量组的线性相关性 第三节向量组的秩 1、极大线性无关向量组 2、矩阵的行秩与列秩 第四节向量空间 1、向量空间 2、向量空间的基、维数3、坐标向量 第五节线性方程组解的结构
本章教学重点:矩阵是线性代数的主要研究对象。它在线性代数与数学的许多分支中都有 重要应用,许多实际问题可用矩阵表示并用有关理论得到解决。本节让学生掌握矩阵的运 算规律及求逆矩阵的方法,要让学生了解矩阵常用的分块方法。 本章教学难点:在于让学生掌握矩阵的运算规律及求逆矩阵的方法,要让学生了解矩阵常 用的分块方法。 教学内容: 第一节 矩阵 1、矩阵 2、矩阵的相等 3、几个常用的特殊矩阵 第二节 矩阵的运算 1、矩阵的加法 2、数与矩阵相乘 3、矩阵与矩阵相乘 4、矩阵的转置 5、方阵的行列式 第三节 逆矩阵 1、逆矩阵的概念 2、逆矩阵的性质 3、方阵的可逆条件与逆矩阵的计算 第四节 分块矩阵 1、分块矩阵 2、分块对角阵 第三章:矩阵的初等变换与线性方程组 本章教学重点:矩阵的初等变换是矩阵的一种重要运算。让学生掌握用矩阵的初等行变换 求矩阵的秩、求逆矩阵、解线性方程组的方法,要让学生了解初等矩阵的作用。 本章教学难点:让学生掌握用矩阵的初等行变换求矩阵的秩、求逆矩阵、解线性方程组的 方法,要让学生了解初等矩阵的作用。 教学内容: 第一节 矩阵的初等变换 1、矩阵的初等变换 2、矩阵等价 3、矩阵的标准型 第二节 初等矩阵 1、初等矩阵 2、利用初等变换求逆矩阵 第三节 矩阵的秩 1、矩阵的秩 2、利用初等变换求矩阵的秩 3、矩阵秩的性质 第四节 线性方程组解的判别法 第四章:向量组的线性相关性 本章教学重点:向量组的线性相关与线性无关是线性代数的重要内容,在此基础上可讨论 线性方程组的通解问题。让学生掌握向量组的线性相关与线性无关的定义及有关的性质, 掌握齐次线性方程组的基础解系和通解的求法,理解非齐次线性方程组解的结构及通解的 概念。 本章教学难点:让学生掌握向量组的线性相关与线性无关的定义及有关的性质,掌握齐次 线性方程组的基础解系和通解的求法,理解非齐次线性方程组解的结构及通解的概念。 教学内容: 第一节 向量组及其线性组合 1、向量的定义及其运算 2、向量的线性组合 3、向量组的线性表示 第二节 向量组的线性相关性 1、线性相关与线性无关 2、向量组的线性相关性 第三节 向量组的秩 1、极大线性无关向量组 2、矩阵的行秩与列秩 第四节 向量空间 1、向量空间 2、向量空间的基、维数 3、坐标向量 第五节 线性方程组解的结构
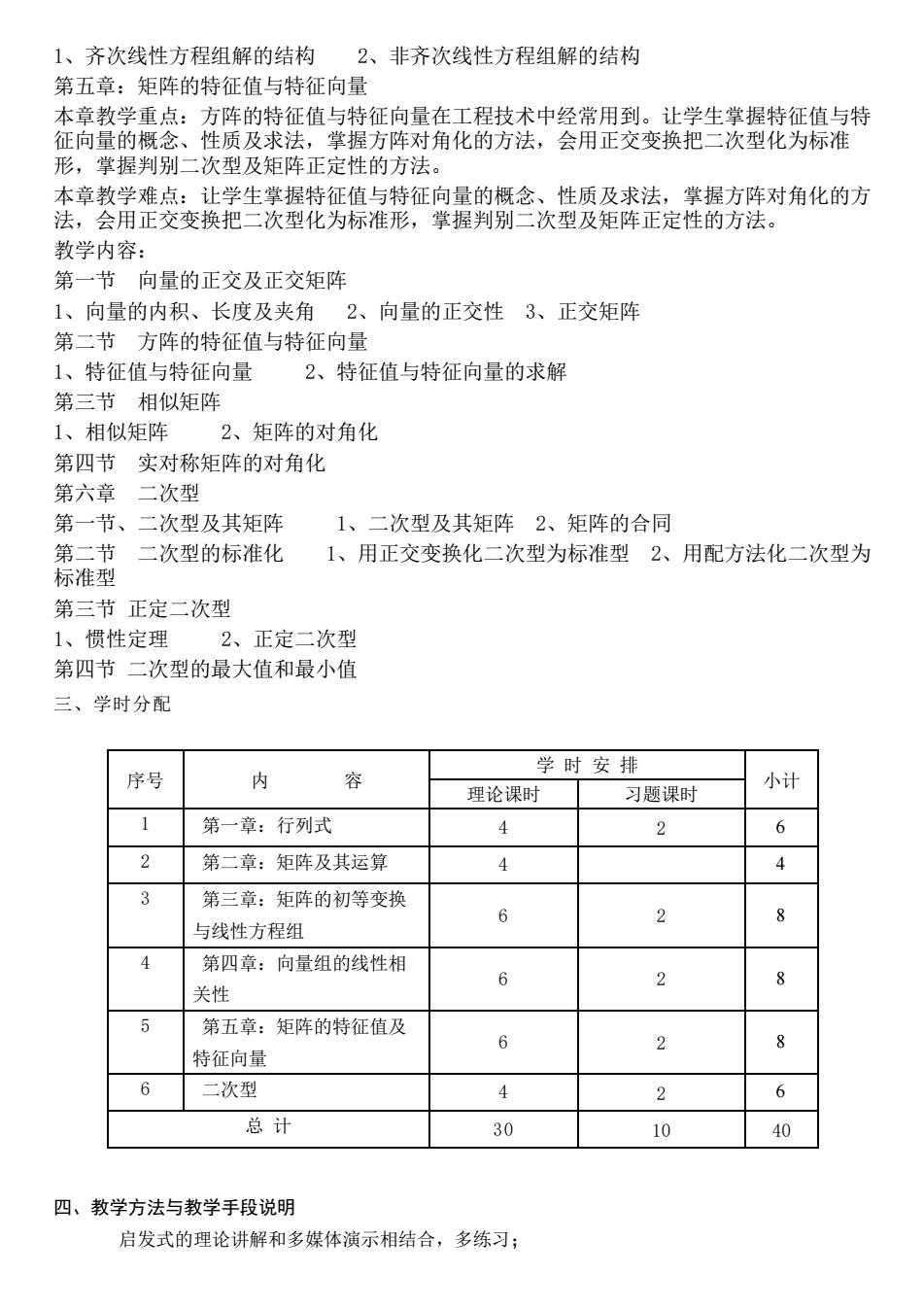
1、齐次线性方程组解的结构2、非齐次线性方程组解的结构 第五章:矩阵的特征值与特征向量 本章教学重点:方阵的特征值与特征向量在工程技术中经常用到。让学生掌握特征值与特 征向量 的概 法 方阵对角化的方法,会用正交变换把二次型化为标准 形,掌握判别二次型及矩阵正定性的方法。 李李整清瓷淡花售委花钙绵楚征家爱纳色x蓝风漆定 、性质及求法,掌握方阵对角化的方 教学内容: 第一节向量的正交及正交矩阵 1、向量的内积、长度及夹角2、向量的正交性3、正交矩阵 第二节方阵的特征值与特征向量 1、特征值与特征向量 2、特征值与特征向量的求解 第三节相似矩阵 1、相似矩阵 2、矩阵的对角化 第四节实对称矩阵的对角化 第六章 一次型 第一节、二次型及其矩阵 1、二次型及其矩阵2、矩阵的合同 第二节 二次型的标准化 1、用正交变换化二次型为标准型2、用配方法化二次型为 标准型 第三节正定二次型 1、惯性定理 2、正定二次型 第四节二次型的最大值和最小值 三、学时分配 的 学时安排 序号 容 理论课时 习题课时 小计 1 第一章:行列式 4 2 6 2 第二章:矩阵及其运算 4 3 第三章:矩阵的初等变换 与线性方程组 6 4 第四章:向量组的线性相 8 关性 6 第五章:矩阵的特征值及 6 8 特征向量 6 二次型 2 6 总计 30 o 0 四、教学方法与教学手段说明 启发式的理论讲解和多媒体演示相结合,多练习;
1、齐次线性方程组解的结构 2、非齐次线性方程组解的结构 第五章:矩阵的特征值与特征向量 本章教学重点:方阵的特征值与特征向量在工程技术中经常用到。让学生掌握特征值与特 征向量的概念、性质及求法,掌握方阵对角化的方法,会用正交变换把二次型化为标准 形,掌握判别二次型及矩阵正定性的方法。 本章教学难点:让学生掌握特征值与特征向量的概念、性质及求法,掌握方阵对角化的方 法,会用正交变换把二次型化为标准形,掌握判别二次型及矩阵正定性的方法。 教学内容: 第一节 向量的正交及正交矩阵 1、向量的内积、长度及夹角 2、向量的正交性 3、正交矩阵 第二节 方阵的特征值与特征向量 1、特征值与特征向量 2、特征值与特征向量的求解 第三节 相似矩阵 1、相似矩阵 2、矩阵的对角化 第四节 实对称矩阵的对角化 第六章 二次型 第一节、二次型及其矩阵 1、二次型及其矩阵 2、矩阵的合同 第二节 二次型的标准化 1、用正交变换化二次型为标准型 2、用配方法化二次型为 标准型 第三节 正定二次型 1、惯性定理 2、正定二次型 第四节 二次型的最大值和最小值 三、学时分配 序号 内 容 学 时 安 排 小计 理论课时 习题课时 1 第一章:行列式 4 2 6 2 第二章:矩阵及其运算 4 4 3 第三章:矩阵的初等变换 与线性方程组 6 2 8 4 第四章:向量组的线性相 关性 6 2 8 5 第五章:矩阵的特征值及 特征向量 6 2 8 6 二次型 4 2 6 总 计 30 10 40 四、教学方法与教学手段说明 启发式的理论讲解和多媒体演示相结合,多练习;

五、考核方式和要求 平时成绩作业课堂纪律占30%,期末考试成绩占70% 六、教材与教学参考书 教材:全国高等农林院校”十一五“规划教材,《线性代数》何东主编,孙冬梅副主编,中国农业出 版社 参考书: 《线性代数》(第三版),同济大学数学教研室编,高等教育出版社 《线性代数辅导》,胡金德等编,清华大学出版社 《高等数学学习指导与解题训练》(线性代数分册),刘学生等主编,大连理工大学出版社
五、考核方式和要求 平时成绩作业课堂纪律占30%,期末考试成绩占70% 六、教材与教学参考书 教材:全国高等农林院校"十一五"规划教材,《线性代数》何东主编,孙冬梅副主编,中国农业出 版社 参考书: 《线性代数》(第三版),同济大学数学教研室编,高等教育出版社 《线性代数辅导》,胡金德等编,清华大学出版社 《高等数学学习指导与解题训练》(线性代数分册),刘学生等主编,大连理工大学出版社