
概率论与数理统计重点与疑 难问题这讲 西部与周边地区大学数学教师暑期研修班 讲课提纲 梅长林 (西安交通大学理学院) 2010.7.26-2010.8.14
概率论与数理统计重点与疑 难问题选讲 西部与周边地区大学数学教师暑期研修班 讲课提纲 梅长林 (西安交通大学理学院) 2010.7.26——2010.8.14

前言 ■内容限于工程数学概率论与数理统计; ■讲授内容不具系统性,只是一些重点和难点以及在授课 中拟引申和展开的内容; ■概率论主要涉及重要概念的引入、理解以及重点需强调 的知识点;数理统计部分主要阐述统计的思想与数学推 理的差异,并简介贝叶斯统计的基本思想以及结合计算 机软件进行统计模拟实验的一些设想; ■对一些内容的处理以及讲授方式只是本人在教学实践中 的一些做法和体会,不妥之处,敬请质疑、讨论; 2010-8-5
2010-8-5 2 一、前言 ◼ 内容限于工程数学概率论与数理统计; ◼ 讲授内容不具系统性,只是一些重点和难点以及在授课 中拟引申和展开的内容; ◼ 概率论主要涉及重要概念的引入、理解以及重点需强调 的知识点;数理统计部分主要阐述统计的思想与数学推 理的差异,并简介贝叶斯统计的基本思想以及结合计算 机软件进行统计模拟实验的一些设想; ◼ 对一些内容的处理以及讲授方式只是本人在教学实践中 的一些做法和体会,不妥之处,敬请质疑、讨论;

二、工程数学概率论写数理统计课程特点 是在大学期间较系统接触的第一门以随机现象为研究对 象的课程,其思想方法(尤其是数理统计的思想方法) 与其他数学课程有较大差异; ■ 本课程内容不具有“自封闭”性,在课程大纲范围内有 些概念不能严格定义,一些定理不能严格证明; ■所涉及的积分多属分段函数以及含参变量的积分,需要 有分段考虑的基本能力: 该课程有强烈应用背景,易于和日常生活中的实际问题 和其他学科领域的问题相结合,便于提高学生的学习兴 趣。 2010-8-5 3
2010-8-5 3 二、工程数学概率论与数理统计课程特点 ◼ 是在大学期间较系统接触的第一门以随机现象为研究对 象的课程,其思想方法(尤其是数理统计的思想方法) 与其他数学课程有较大差异; ◼ 本课程内容不具有“自封闭”性,在课程大纲范围内有 些概念不能严格定义,一些定理不能严格证明; ◼ 所涉及的积分多属分段函数以及含参变量的积分,需要 有分段考虑的基本能力; ◼ 该课程有强烈应用背景,易于和日常生活中的实际问题 和其他学科领域的问题相结合,便于提高学生的学习兴 趣

三、上好第一节课 1.从两个简单实验的对北比引出随机试验和随机现象 实验I:袋中有10个形状完全相同的红球,搅匀后从中任 取一个,所取出球的颜色如何? 实验II:袋中有10个形状完全相同的红球,其中6个白球 4个红球,搅匀后从中任取一个,所取出球的颜 色如何? 2010-8-5 4
2010-8-5 4 三、上好第一节课 1.从两个简单实验的对比引出随机试验和随机现象 实验I: 袋中有10个形状完全相同的红球,搅匀后从中任 取一个,所取出球的颜色如何? 实验II: 袋中有10个形状完全相同的红球,其中6个白球 4个红球,搅匀后从中任取一个,所取出球的颜 色如何?

三、上好第一节课 实验II的特点: (1)实验可以在相同的条件下重复进行; (2)实验的所有结果明确可知,且不止一个: (3) 每次试验总是恰好出现这些结果中的一个,但 在实验之前不能断定到底会出现那一个结果。 满足上述三条的实验随机试验 随机试验描述的现象一随机现象 概率论从数量角度研究随机现象的规律 2010-8-5
2010-8-5 5 三、上好第一节课 实验II的特点: (1)实验可以在相同的条件下重复进行; (2)实验的所有结果明确可知,且不止一个; (3)每次试验总是恰好出现这些结果中的一个,但 在实验之前不能断定到底会出现那一个结果。 满足上述三条的实验 随机试验 随机试验描述的现象 随机现象 概率论 从数量角度研究随机现象的规律

三、上好第、节课 2.随机现象的统计规律性 (1)将实验II重复进行多次,取到的白球数:红球数近 似6:4。 (2)连续投掷一枚均匀硬币,正反面出现的次数近似相 等(参见下表的历史记录)。 2010-8-5 6
2010-8-5 6 三、上好第一节课 2. 随机现象的统计规律性 (1)将实验II重复进行多次,取到的白球数:红球数近 似6:4。 (2)连续投掷一枚均匀硬币,正反面出现的次数近似相 等(参见下表的历史记录)
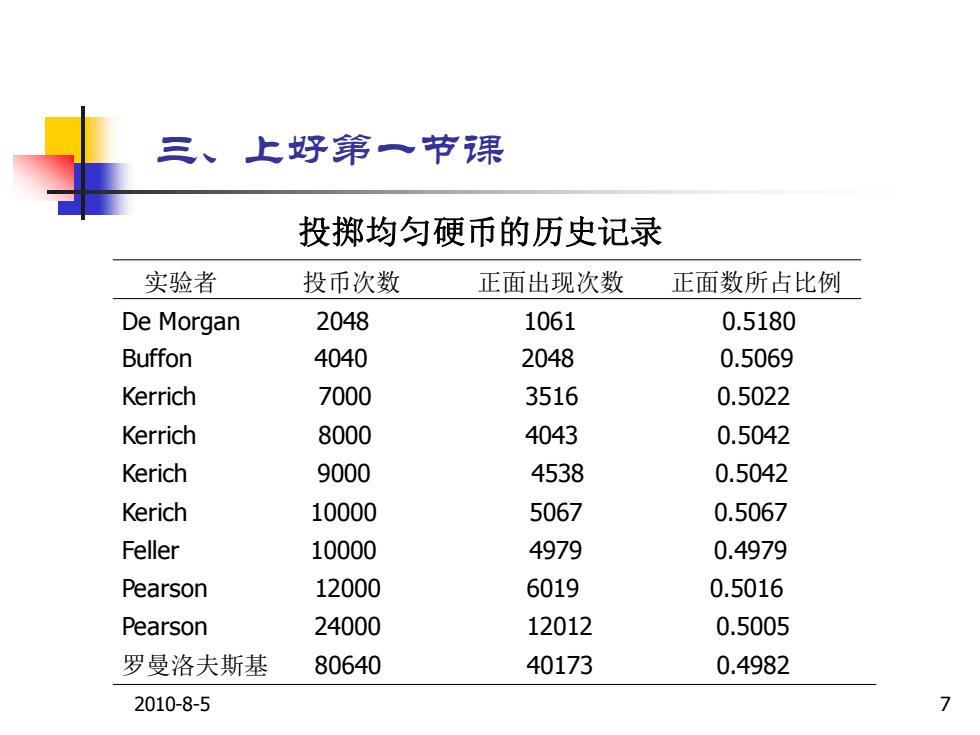
三、上好第一节课 投掷均匀硬币的历史记录 实验者 投币次数 正面出现次数 正面数所占比例 De Morgan 2048 1061 0.5180 Buffon 4040 2048 0.5069 Kerrich 7000 3516 0.5022 Kerrich 8000 4043 0.5042 Kerich 9000 4538 0.5042 Kerich 10000 5067 0.5067 Feller 10000 4979 0.4979 Pearson 12000 6019 0.5016 Pearson 24000 12012 0.5005 罗曼洛夫斯基 80640 40173 0.4982 2010-8-5 7
2010-8-5 7 三、上好第一节课 实验者 投币次数 正面出现次数 正面数所占比例 De Morgan 2048 1061 0.5180 Buffon 4040 2048 0.5069 Kerrich 7000 3516 0.5022 Kerrich 8000 4043 0.5042 Kerich 9000 4538 0.5042 Kerich 10000 5067 0.5067 Feller 10000 4979 0.4979 Pearson 12000 6019 0.5016 Pearson 24000 12012 0.5005 罗曼洛夫斯基 80640 40173 0.4982 投掷均匀硬币的历史记录
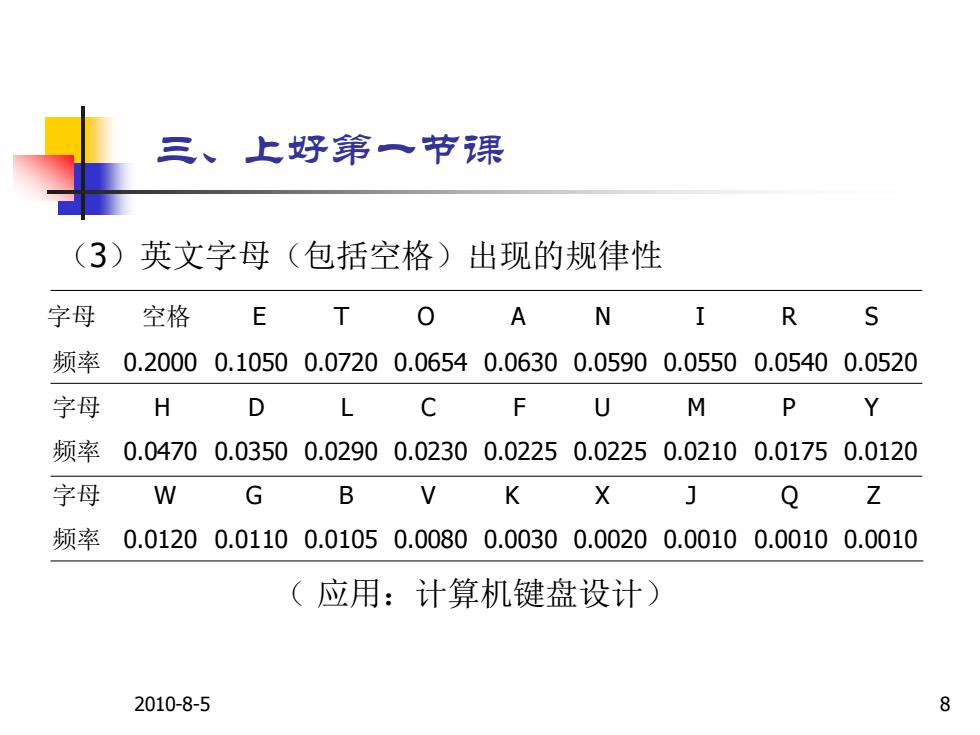
三、上好第一节课 (3)英文字母(包括空格)出现的规律性 字母 空格 E T 0 A N I R S 频率0.20000.10500.07200.06540.06300.05900.05500.05400.0520 字母 H D L C F U M P Y 频率 0.04700.03500.02900.02300.02250.02250.02100.01750.0120 字母 W G B V K X Q Z 频率0.01200.01100.01050.00800.00300.00200.00100.00100.0010 (应用:计算机键盘设计) 2010-8-5 8
2010-8-5 8 三、上好第一节课 (3)英文字母(包括空格)出现的规律性 字母 空格 E T O A N I R S 频率 0.2000 0.1050 0.0720 0.0654 0.0630 0.0590 0.0550 0.0540 0.0520 字母 H D L C F U M P Y 频率 0.0470 0.0350 0.0290 0.0230 0.0225 0.0225 0.0210 0.0175 0.0120 字母 W G B V K X J Q Z 频率 0.0120 0.0110 0.0105 0.0080 0.0030 0.0020 0.0010 0.0010 0.0010 ( 应用:计算机键盘设计)

三、上好第一节课 3工概率论发展简史 概率论的概念形成于16世纪,与投掷骰子的赌博方式有关; Fermat(法国,1601-1665)和Pascal(法国:1623-1662) 的通信被认为是建立概率论数学基础的起点,二人被称为是概 率论的奠基人。 促使Fermat和Pascal通信的人是De Mere(法国:1601- 1665)。 瑞士Bernoul1i家族至少有5人在概率论方面做出重要贡献。 Ko1 mogorov(俄国:1903-1987)在1933年建立了概率的公理 化体系。 我困海宝騄教授(1910-1970)在概率统计研究方面贡献突出g
2010-8-5 9 三、上好第一节课 3. 概率论发展简史 概率论的概念形成于16世纪,与投掷骰子的赌博方式有关; Fermat(法国,1601-1665)和 Pascal(法国:1623-1662) 的通信被认为是建立概率论数学基础的起点,二人被称为是概 率论的奠基人。 促使Fermat和Pascal通信的人是De Mere(法国: 1601- 1665 )。 瑞士Bernoulli家族至少有5人在概率论方面做出重要贡献。 Kolmogorov(俄国:1903-1987)在1933年建立了概率的公理 化体系。 我国许宝騄教授(1910-1970)在概率统计研究方面贡献突出

三、上好第一节课 4.一些概率(统计)实例 (1)De Mere问题:一赌徒以“一枚骰子连掷4次,均不出‘6' 点”与庄家打赌,赌徒的条件是否对他有利?进一步,“两枚骰子连 掷,需多少次,均不出双‘6’的概率会小于至少出现一次双‘6’ 的概率”? (2)赌徒破产问题:一赌徒有本金a元,计划再赢b元就停止赌 博。设赌徒每局赢的概率p=0.5,每局输赢都是一元钱,赌徒输光后停 止赌博,赌徒输光的概率q(a)是多少? (结果:q(a)=b/b+a:若a有限,赌徒贪心b越大,输光的 概率越大;如果一直赌下去(b趋于无穷),赌徒必定输光。)】 2010-8-5 10
2010-8-5 10 三、上好第一节课 4. 一些概率(统计)实例 (1)De Mere问题:一赌徒以“一枚骰子连掷4次,均不出‘6’ 点”与庄家打赌,赌徒的条件是否对他有利?进一步,“两枚骰子连 掷,需多少次,均不出双‘6’的概率会小于至少出现一次双‘6’ 的概率”? (2) 赌徒破产问题:一赌徒有本金a元,计划再赢b元就停止赌 博。设赌徒每局赢的概率p=0.5,每局输赢都是一元钱,赌徒输光后停 止赌博,赌徒输光的概率q(a)是多少? (结果:q(a)=b/(b+a): 若a有限,赌徒贪心b越大,输光的 概率越大;如果一直赌下去(b趋于无穷),赌徒必定输光。)