《概率论与数理统计》课程教学资源（PPT课件）第二章 随机变量及其分布 第五节 随机变量的函数的分布

概華论与款程统外 第五节随机变量的函数的分布 一、离散型随机变量的函数的分布 二、连续型随机变量的函数的分布 三、小结

一、离散型随机变量的函数的分布 二、连续型随机变量的函数的分布 三、小结 第五节 随机变量的函数的分布

概车纶与散理统针「 一、离散型随机变量的函数的分布 设f(x)是定义在随机变量X的一切可能值 x的集合上的函数，若随机变量Y随着X取值x 的值而取y=f(x)的值，则称随机变量Y为随机 变量X的函数，记作Y=f(X). 问题 如何根据己知的随机变量X的 分布求得随机变量Y=f(X)的分布？

, ( ). ( ) , , ( ) X Y f X y f x Y x Y X x f x X = = 变量 的函数 记作 的值而取 的值 则称随机变量 为随机 的集合上的函数 若随机变量 随着 取值 设 是定义在随机变量 的一切可能值 问题 分布求得随机变量 ( )的分布? 如何根据已知的随机变量 的 Y f X X = 一、离散型随机变量的函数的分布

概華论与款醒硫外 例1设X的分布律为 X-1012 1111 4444 求Y=X2的分布律 解Y的可能值为(-1)2,02,12,22； 即0,1,4. PY=0}=PX2=0}=P{X=0}=4 1

Y 的可能值为 ( 1) , 0 , 1 , 2 ; 2 2 2 2 − 即 0, 1, 4. 解 { 0} { 0} { 0} 2 P Y = = P X = = P X = , 4 1 = . 求 2 的分布律 设 的分布律为 Y X X = X p − 1 0 1 2 4 1 4 1 4 1 4 1 例1

概车纶与款理统外 P{Y=1}=P{X2=1}=P{X=-1)U(X=1)} =PX=-1+PX==+1=1, 442 PY=4=P{X2=4}=P{X=2=4 014 故Y的分布律为 111 424 由此归纳出离散型随机变量函数的分布的求法

{ 1} { 1} {( 1) ( 1)} 2 P Y = = P X = = P X = −  X = = P{X = −1}+ P{X = 1} , 2 1 4 1 4 1 = + = { 4} { 4} { 2} 2 P Y = = P X = = P X = , 4 1 = 故 Y 的分布律为 Y p 0 1 4 4 1 2 1 4 1 由此归纳出离散型随机变量函数的分布的求法

概率伦与款程统外 离散型随机变量的函数的分布 如果X是离散型随机变量，其函数Y=g(X) 也是离散型随机变量若X的分布律为 X x x2 Xk Pk P2 Pk 则Y=g(X)的分布律为 Y=g(X)） 8(x1)g(x2) .g(xk) . Pk P P2 Pk 若g(x)中有值相同的应将相应的p合并

离散型随机变量的函数的分布 也是离散型随机变量 若 的分布律为 如果 是离散型随机变量 其函数 X X Y g X . , = ( ) X pk x1 x2  xk  p1 p2  pk  则Y = g(X)的分布律为 pk Y = g(X) p1 p2  pk  g(x1 ) g(x2 )  g(xk )  若 ( )中有值相同的,应将相应的 合并. g xk pk

概车纶与款理统外 X 一1 1 2 例2设 3 6 2-6 6 求Y=X-5的分布律. 解Y的分布律为 4 1 1 2 2

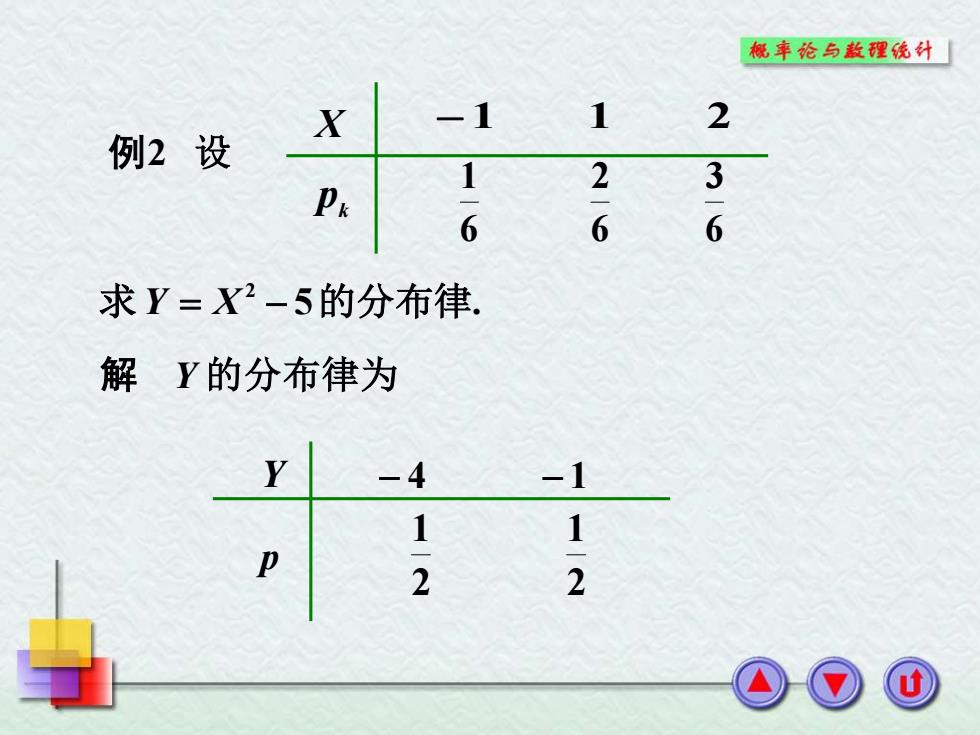
Y 的分布律为 Y p − 4 − 1 2 1 2 1 X k p − 1 1 2 6 1 6 2 6 3 例2 设 5 . 求Y = X 2 − 的分布律 解

概率纶与款理统外「 二、连续型随机变量的函数的分布 例3 设随机变量X的概率密度为 Jx(x)= P, 0<x<4, 0,其他. 求随机变量Y=2X+8的概率密度： 解第一步先求Y=2X+8的分布函数F,(y) F,(y)=P{Y≤y}=P{2X+8≤y}

第一步 先求Y=2X+8 的分布函数 F ( y). Y F ( y) P{Y y} Y =  = P{2X + 8  y} 解 二、连续型随机变量的函数的分布 2 8 . 0, . , 0 4, ( ) 8 求随机变量 的概率密度 其他 设随机变量 的概率密度为 = +       = Y X x x f x X X 例3

概车纶与款理统外 =Px≤'2=dx 第二步由分布函数求概率密度 fy(y)=F,(y) fx(x)dxr =2828

f ( y) F ( y) Y y =  f x x y X ( )d 2 8  − − }= 2 8 { − =  y P X ) , 2 8 )( 2 8 ( − −  = y y fX 第二步 由分布函数求概率密度. [ ( )d ] 2 8 =   − − f x x y X

概率伦与款理统外 所以0-传3生4 2 0, 其他. y-8 8<y<16, 32 0, 其他

      −   − = 0, . 4, 2 8 , 0 2 1 ) 2 8 ( 8 1 ( ) 其他 所以 y y f y Y        − = 0, . , 8 16, 32 8 其他 y y

概车纶与款理统外 例4设随机变量X的概率密度为 x<0, 求随机变量Y=X2和Y=2X+3的概率密度 解先求随机变量Y=X分布函数， F,(y)=PY≤y=P{X2≤y} =P{-V≤X≤√y =Fx(Ny)-Fx(-√y)

F ( y) P{Y y} Y =  { } 2 = P X  y = P{− y  X  y} F ( y) F ( y) = X − X − 2 3 . e , 0. 0, 0, ( ) 23 2 求随机变量 和 的概率密度 设随机变量 的概率密度为 = = +   = − Y X Y X x xx f x X X x 解 , 先求随机变量Y = X2 分布函数 例 4