
概華论与款醒硫外 第六章 样本及抽样分布 习题课 一、重点与难点 二、主要内容 三、典型例题
第六章 样本及抽样分布 习 题 课 二、主要内容 三、典型例题 一、重点与难点

概车纶与款理统外 一、重点与难点 1.重点 (1)正态总体某些常用统计量的分布. (2)临界值的查表计算, 2.难点 ()几个常用统计量的构造。 (2)标准正态分布和F分布临界值的查表计算
一、重点与难点 1.重点 (1) 正态总体某些常用统计量的分布. 2.难点 (1) 几个常用统计量的构造. (2) 临界值的查表计算. (2) 标准正态分布和F分布临界值的查表计算
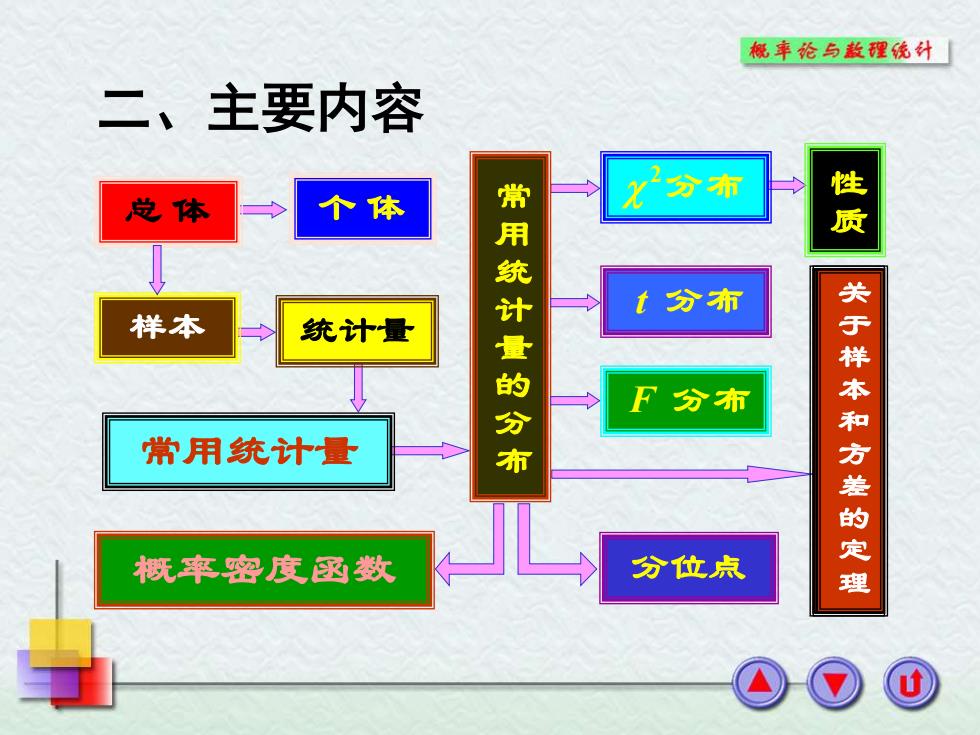
概率纶与款醒统外「 二、主要内容 个体 X2分肃 总体 性 常用统计量的分布 t分布 样本 统计量 F分布 常用统计量 关于样本和方差的定理 概率密度极数 分位点
总 体 个 体 样本 常用统计量的分布 概率密度函数 分位点 二、主要内容 统计量 常用统计量 性质关于样本和方差的定理 t 分布 F 分布 2 分布 关于样本和方差的定理

概车纶与款理统外 总体 试验的全部可能的观察值称为总体 个体 总体中的每个可能观察值称为个体
总体 试验的全部可能的观察值称为总体. 个体 总体中的每个可能观察值称为个体

概華论与款醒硫外 样本 设X是具有分布函数F的随机变量,若X, X2,.,Xn是具有同一分布函数F、相互独立的 随机变量,则称X1,X2,Xn为从分布函数F (或总体F、或总体X)得到的容量为n的简单 随机样本,简称样本
样本 , . ( ) , , , , , , , , 1 2 2 1 随机样本 简称样本 或总体 、或总体 得到的容量为 的简单 随机变量 则 称 为从分布函数 是具有同一分布函数 、相互独立的 设 是具有分布函数 的随机变量 若 F X n X X X F X X F X F X n n

概车纶与款理统外 统计量 设X1,X2,.,Xn是来自总体X的一个样本 g(X1,X2,.,Xn)是X1,X2,.,Xn的函数,若g中 不含未知参数则称g(X1,X2,.,Xn)是一个统 计量
统计量 . , ( , , , ) ( , , , ) , , , , , , , , 1 2 1 2 1 2 1 2 计 量 不含未知参数 则 称 是一个统 是 的函数 若 中 设 是来自总体 的一个样本 n n n n g X X X g X X X X X X g X X X X

概率伦与款程统外 常用统计量 样本平均值:X=之x n i=1 (2)样本方差: s-2x-〔含- 3)样本标准差: ==a2x-
常用统计量 (1)样本平均值: . 1 1 = = n i Xi n X (2)样本方差: = − − = n i Xi X n S 1 2 2 ( ) 1 1 . 1 1 1 2 2 − − = = n i Xi nX n (3)样本标准差: ( ) . 1 1 1 2 2 = − − = = n i Xi X n S S

概车纶与款理统外 常用统计量 4样本k阶(原点矩:4,=∑X,k=1,2,. n i=1 (⑤)样本k阶中心矩: 8=2x-0,k=2,3 n i=i
常用统计量 (4)样本 k 阶(原点)矩: , 1, 2, . 1 1 = = = X k n A n i k k i (5)样本 k 阶中心矩: ( ) , 2, 3, . 1 1 = − = = X X k n B n i k k i

概率伦与款程统外 常用统计量的分布(一) x分布 设X1,X2,Xn是来自总体N(0,1)的样 本,则称统计量x2=X?+X?++X7服从自 由度为n的x2分布,记为x2~x2(n)
常用统计量的分布(一) 2分布 , ~ ( ). , , , , (0, 1) 2 2 2 2 2 2 2 1 2 1 2 n n X X X X X X N n n 由度为 的 分 布 记 为 本 则称统计量 = 服从自 设 是来自总体 的 样 + ++

概车纶与款理统外 X分布的性质 性质1(x分布的可加性) 设~x2(n1),~x2(2),并且,2独 立,则x+2~x2(n1+ 性质2(x分布的数学期望和方差) 若x2~x2(n),则E(x2)=n,D(x2)=2n
分布的性质 2 性质1 , ~ ( ). ~ ( ), ~ ( ), , 1 2 2 2 2 2 1 2 2 2 2 1 2 2 1 2 2 2 1 n n n n + + 立 则 设 并 且 独 ( ) 2分布的可加性 性质2 ~ ( ), ( ) , ( ) 2 . 2 2 2 2 若 n 则 E = n D = n ( ) 2分布的数学期望和方差