
概華论与款醒硫外「 第四节矩、协方差矩阵 一、基本概念 二、n维正态变量的性质 三、小结
一、基本概念 二、n 维正态变量的性质 三、小结 第四节 矩、协方差矩阵

概车纶与款理统外 一、基本概念 1.定义 设X和Y是随机变量,若E(X“),k=1,2, 存在,称它为X的k阶原点矩简称k阶矩 若E{X-E(X)},k=2,3,. 存在,称它为X的k阶中心矩 若E(X“Y),k,1=1,2,. 存在,称它为X和Y的k+I阶混合矩 若EIX-E(X)川[Y-E(Y)'},k,1=1,2,. 存在,称它为X和Y的k+I阶混合中心矩
, , . , ( ), 1,2, X k 阶原点矩 k 阶 矩 X Y E X k k 存在 称它为 的 简称 设 和 是随机变量 若 = , . {[ ( )] }, 2,3, X k 阶中心矩 E X E X k k 存在 称它为 的 若 − = , . ( ), , 1,2, X Y k l阶混合矩 E X Y k l k l + = 存在 称它为 和 的 若 一、基本概念 1.定义 , . {[ ( )] [ ( )] }, , 1,2, X Y k l 阶混合中心矩 E X E X Y E Y k l k l + − − = 存在 称它为 和 的 若

概率伦与款程统外 2.说明 ()以上数字特征都是随变量函数的数学期望 (2)随机变量X的数学期望E(X)是X的一阶原 点矩,方差为二阶中心矩,协方差CoV(X,Y)是X 与Y的二阶混合中心矩; (3)在实际应用中高于4阶的矩很少使用 三阶中心矩E{X-E(X)}主要用来衡量随 机变量的分布是否有偏. 四阶中心矩EX-E(X)4}主要用来衡量随 机变量的分布在均值附近的陡峭程度如何
2. 说明 ; , , Cov( , ) (2) ( ) 与 的二阶混合中心矩 点矩 方差为二阶中心矩 协方差 是 随机变量 的数学期望 是 的一阶原 Y X Y X X E X X (1)以上数字特征都是随机变量函数的数学期望; (3) 在实际应用中,高于4阶的矩很少使用. . {[ ( )] } 3 机变量的分布是否有偏 三阶中心矩E X − E X 主要用来衡量随 . {[ ( )] } 4 机变量的分布在均值附近的陡峭程度如何 四阶中心矩 E X − E X 主要用来衡量随

概车纶与款理统外 3.协方差矩阵 设n维随机变量(X1,X2,.,Xm)的二阶混合 中心矩 ci Cov(Xi,X )=E(IX;-E(Xi)IX;-E(X ) i,j=1,2,.,n 都存在,则称矩阵 Cu C12 .Cin C= C21 C22 Cnl Cn2 C 为n维随机变量的协方差矩阵
3. 协方差矩阵 中心矩 设 n 维随机变量(X1 , X2 ,, Xn )的二阶混合 , , 1,2, , Cov( , ) {[ ( )][ ( )] 都存在 i j n cij Xi X j E Xi E Xi X j E X j = = = − − 则称矩阵 = n n nn n n c c c c c c c c c C 1 2 21 22 2 11 12 1 为 n 维随机变量的协方差矩阵

概華论与款醒硫外 例如二维随机变量(X1,X2)的协方差矩阵为 c= 其中c1=E{IX1-E(X1)3, Ci2=E{IXI-E(X )IX2-E(X2)B, C21=E{X2-E(X2)X1-E(X1)}, C22=E{X2-E(X2)I}
例如 二维随机变量(X1 ,X2 )的协方差矩阵为 = 21 22 11 12 c c c c C {[ ( )] }, 2 1 1 E X1 E X1 其中 c = − {[ ( )][ ( )]}, 12 E X1 E X1 X2 E X2 c = − − {[ ( )][ ( )]}, 21 E X2 E X2 X1 E X1 c = − − {[ ( )] }. 2 22 E X2 E X2 c = −

概率伦与散理统针」 由于c=ci(i,j=1,2,.,n),所以协方差矩 阵为对称的非负定矩阵 协方差矩阵的应用 协方差矩阵可用来表示多维随 机变量的概率密度,从而可通 过协方差矩阵达到对多维随机 变量的研究
. ( , 1,2, , ) , 阵为对称的非负定矩阵 由于 cij = c ji i j = n 所以协方差矩 协方差矩阵的应用 协方差矩阵可用来表示多维随 机变量的概率密度,从而可通 过协方差矩阵达到对多维随机 变量的研究

概華论与款程统外 以二维随机变量(X1,X2)为例. 由于 1 f(xu)=2ng0:1-p rm“-. 0102 引入电库x-)r-) 及(X1,X2)的协方差矩阵C=
( , ) . 以二维随机变量 X1 X2 为例 . ( )( ) ( ) 2 ( ) 2(1 ) 1 exp 2π 1 1 ( , ) 2 2 2 2 2 1 2 1 1 2 2 2 1 2 1 1 2 2 1 2 1 2 − + − − − − − − − = σ x μ σ σ x μ x μ ρ σ x μ ρ σ σ ρ f x x 由于 引入矩阵 , 2 1 = x x X . 2 1 = μ μ μ 及 (X1 , X2 )的协方差矩阵 , 21 22 11 12 = c c c c C
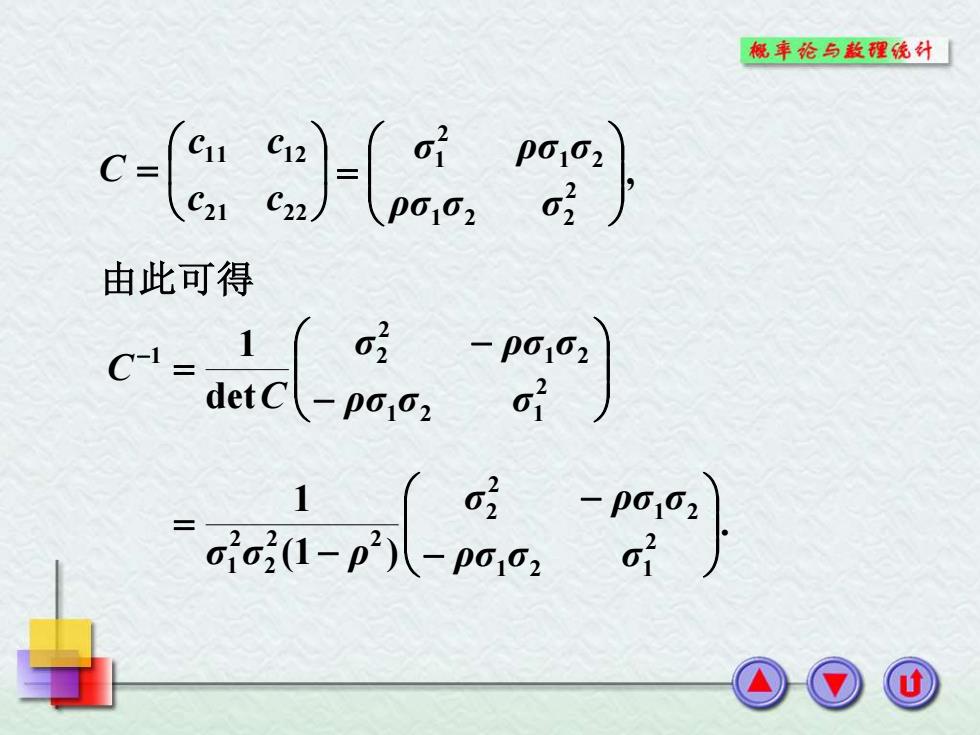
概车纶与款理统外 c-gHa} 由此可得 -D0102 1 =ag(1=p)-0503 -p102
= 21 22 11 12 c c c c C , 2 1 2 2 1 2 2 1 = ρσ σ σ σ ρσ σ 由此可得 − − = − 2 1 2 1 1 2 2 1 2 det 1 ρσ σ σ σ ρσ σ C C . (1 ) 1 2 1 2 1 1 2 2 2 2 2 2 2 1 − − − = ρσ σ σ σ ρσ σ σ σ ρ

概華论与款醒硫外 由于 (X-)TC-(X-) lCw-A出- -p0102 o102 =-
− − − − = − − − − − 2 2 1 1 2 1 2 1 1 2 2 2 1 1 2 2 T 1 ( , ) det 1 ( ) ( ) x μ x μ ρσ σ σ σ ρσ σ x μ x μ C X μ C X μ . ( )( ) ( ) 2 ( ) 1 1 2 2 2 2 2 1 2 1 1 2 2 2 1 2 1 1 2 − + − − − − − = σ x μ σ σ x μ x μ ρ σ x μ ρ 由于

概车纶与款理统外 于是(X1,X2)的概率密度可写成 f(x1,x2) 2nrdosnfx-nrc'x-l
于是(X1 ,X2 )的概率密度可写成( ) ( ) . 2 1 exp (2π) (det ) 1 ( , ) 1 2 2 1 2 1 2 = − − − − X μ C X μ C f x x T