
概率伦与数理统外「 第二节 中心极限定理 一、问题的引入 二、基本定理 三、典型例题 四、小结
第二节 中心极限定理 一、问题的引入 二、基本定理 三、典型例题 四、小结

概華伦与款程统外 一、问题的引入 实例:考察射击命中点与靶心距离的偏差 这种偏差是大量微小的偶然因素造成的微 小误差的总和,这些因素包括:瞄准误差、测量 误差、子弹制造过程方面(如外形、重量等)的 误差以及射击时武器的振动、气象因素(如风速、 风向、能见度、温度等)的作用,所有这些不同 因素所引起的微小误差是相互独立的,并且它们 中每一个对总和产生的影响不大。 问题:某个随机变量是由大量相互独立且均匀 小的随机变量相加而成的,研究其概率分布情况
一、问题的引入 实例: 考察射击命中点与靶心距离的偏差. 这种偏差是大量微小的偶然因素造成的微 小误差的总和, 这些因素包括: 瞄准误差、测量 误差、子弹制造过程方面 (如外形、重量等) 的 误差以及射击时武器的振动、气象因素(如风速、 风向、能见度、温度等) 的作用, 所有这些不同 因素所引起的微小误差是相互独立的, 并且它们 中每一个对总和产生的影响不大. 问题: 某个随机变量是由大量相互独立且均匀 小的随机变量相加而成的, 研究其概率分布情况

概车纶与款理统外 二、基本定理 定理四(独立同分布的中心极限定理) 设随机变量X1,X2,.,Xm,.相互独立服从 同一分布,且具有数学期望和方差:E(X)=4, D(X)=o2>0(k=1,2,则随机变量之和的 立x-2xx-w 标准化变量Y,= k=1 2x
二、基本定理 定理四(独立同分布的中心极限定理) 则随机变量之和的 同一分布 且具有数学期望和方差: 设随机变量 相互独立 服 从 ( ) 0 ( 1,2, ), , ( ) , , , , , , 2 1 2 = = = D X k E X X X X k k n − = = = = n k k n k k n k k n D X X E X Y 1 标准化变量 1 1 n X n n k k − = =1

概率伦与款理统外 的分布函数F(x)对于任意x满足 :-nu lim F(x)=limP每 ≤X n-→oo no 2 定理四表明: 当n→oo,随机变量序列Y,的分布函数收敛于 标准正态分布的分布函数
− = = → → x n X n F x P F x x n k k n n n n 1 lim ( ) lim 的分布函数 ( ) 对于任意 满 足 定理四表明: . , 标准正态分布的分布函数 当n → 随机变量序列Yn 的分布函数收敛于 − − = = x t e dt (x). 2π 1 2 2

概车纶与款理统外 定理五(李雅普诺夫定理) 李雅普诺夫 设随机变量X1,X2,.,Xm,.相互独立它 们具有数学期望和方差: E(Xk)=4k,D(Xk)=Ok2≠0(k=1,2,), 记 B=∑o, k=1 若存在正数6,使得当n→o时, 2X4”-→0
{| | } 0, 1 , , , ( ) , ( ) 0 ( 1,2, ), , , , , , 1 2 2 1 2 2 2 1 2 − → → = = = = = + + = n k k k n n k n k k k k k n E X B n B E X D X k X X X 若存在正数 使得当 时 记 们具有数学期望和方差: 设随机变量 相互独立 它 定理五(李雅普诺夫定理) 李雅普诺夫
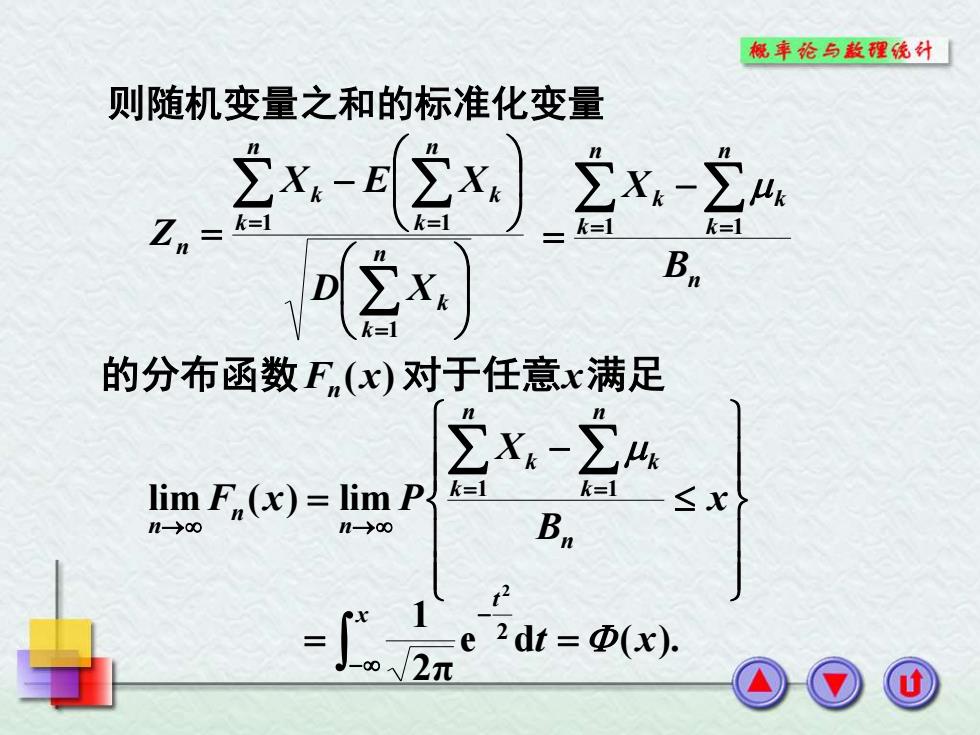
概率伦与款醒统外「 则随机变量之和的标准化变量 x-2x2x-24 k=1 2x B 的分布函数F(x)对于任意x满足 ∑x-∑4 lim F((x)=lim P每 k=1 ≤X〉
则随机变量之和的标准化变量 − = = = = n k k n k k n k k n D X X E X Z 1 1 1 n n k k n k k B X = = − = 1 1 的分布函数Fn (x)对于任意x满足 − = = = → → x B X F x P n n k k n k k n n n 1 1 lim ( ) lim − − = = x t e dt (x). 2π 1 2 2

概车纶与款理统外 定理五表明: 无论各个随机变量X1,X2,.,Xm,.服从什么 分布,只要满足定理的条件,那么它们的和∑X。 k=1 当n很大时,近似地服从正态分布. (如实例中射击偏差服从正态分布) 下面介绍的定理六是定理四的特殊情况
定理五表明: , . , , , , , , 1 1 2 当 很大时 近似地服从正态分布 分布 只要满足定理的条件 那么它们的和 无论各个随机变量 服从什么 n X X X X n k k n = (如实例中射击偏差服从正态分布) 下面介绍的定理六是定理四的特殊情况

概華论与款醒硫外 定理六(德莫佛一拉普拉斯定理) 德莫佛 拉普拉斯 设随机变量nn(n=1,2,)服从参数为n,p (0<p<1)的二项分布,则对于任意x,恒有 Ps小上2ar-ow 证明 根据第四章第二节例题可知,=∑X, k=1 其中X1,X2,.,Xn是相互独立的、服从同一 (0一1)分布的随机变量,分布律为 PXk=i}=p(1-p)-, i=0,1
− − → = = − − = x t n n n x t x np p np P p x n n p e d ( ). 2π 1 (1 ) lim (0 1) , , ( 1,2, ) , 2 2 的二项分布 则 对于任意 恒有 设随机变量 服从参数为 证明 根据第四章第二节例题可知 , 1 = = n k n Xk - 分布的随机变量 分布律为 其中 是相互独立的、服从同一 (0 1) , , , , X1 X2 Xn { } (1 ) , 0, 1. 1 = = − = − P X i p p i i i k 定理六(德莫佛-拉普拉斯定理) 德莫佛 拉普拉斯

概车纶与款理统外「 .E(Xk)=p,D(Xk)=p(1-p)(k=1,2,.,n), 根据定理四得 e 2dt =(x). 定理六表明: 正态分布是二项分布的极限分布,当n充分大 时,可以利用该定理来计算二项分布的概率
E(X ) p, k = D(X ) p(1 p) (k 1,2, ,n), k = − = 根据定理四得 = − − → x np p np P n n (1 ) lim − − = → x np p X np P n k k n (1 ) lim 1 − − = = x t e dt (x). 2π 1 2 2 定理六表明: 正态分布是二项分布的极限分布, 当n充分大 时, 可以利用该定理来计算二项分布的概率
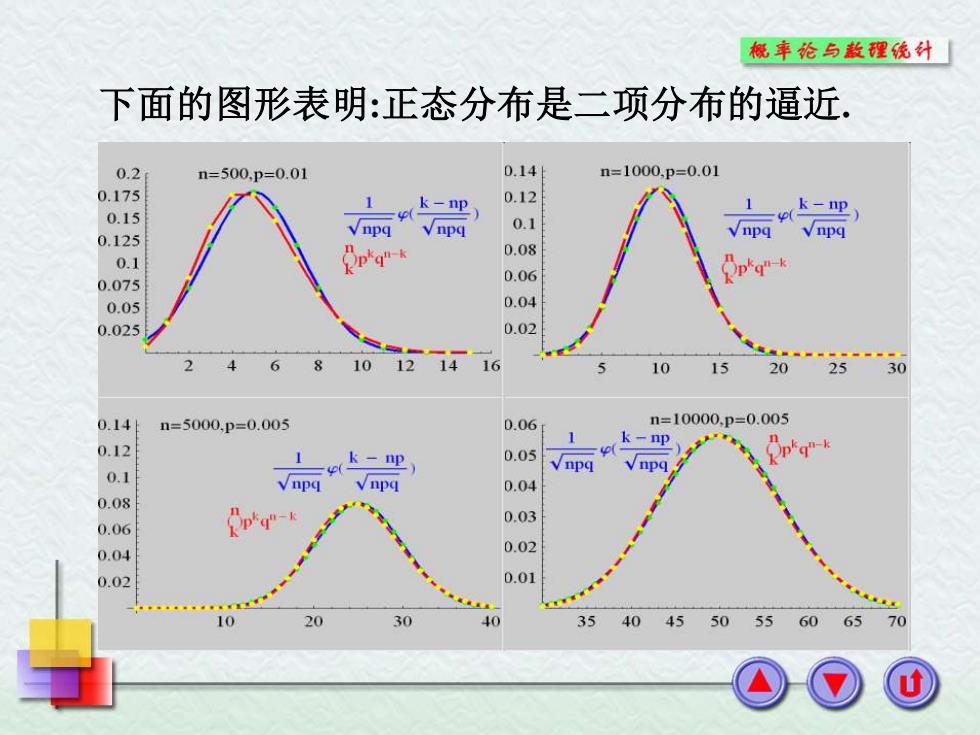
概華论与款醒硫外 下面的图形表明:正态分布是二项分布的逼近, 0.2 n=500,p=0.01 0.14 n=1000,p=0.01 0.175 k-np 0.12 1 0.15 k-np 0.1 0.125 Vpg√pg 0.08 0.1 0.075 0.06 0.05 0.04 0.025 0.02 6 8 101214i6 10 15 20 25 30 0.14 n=5000,p=0.005 0.06 n=10000,p=0.005 1 0.12 k-np 1 0.05 0.1 0.04 0.08 p-s 0.03 0.06 0.04 0.02 0.02 0.01 . 10 20 30 40 35 4045505560 6570
下面的图形表明:正态分布是二项分布的逼近