
第一章随机事件和糯年 §1.1 随机事件 §1.2 概率的定义 §1.3 条件概率、全概率公式和 贝叶斯公式 §1.4 事件的独立性 §1.5 伯努利(Bernoulli)概型 2024年8月27日星期二 1 目录○ 上页 下页 返回
2024年8月27日星期二 1 目录 上页 下页 返回 第一章 随机事件和概率 §1.1 随机事件 §1.2 概率的定义 §1.3 条件概率、全概率公式和 贝叶斯公式 §1.4 事件的独立性 §1.5 伯努利(Bernoulli)概型

主要内容 古典 随机 随机事件 概率 概型 现家 必 对 定 性 合事 本 然 随机 不可能事 几何 立事 义 质 概率 事 试验 件 件 件 件 条件 乘法 事件的 事件的关系和运算 概率 定理 独立性 全概率公式与贝叶斯公式 2024年8月27日星期二 2 目录○ 上页下页 返回
2024年8月27日星期二 2 目录 上页 下页 返回 主要内容 随机 现象 随机 试验 事件的 独立性 随 机 事 件 基 本 事 件 必 然 事 件 对 立 事 件 概 率 古典 概型 几何 概率 乘法 事件的关系和运算 定理 全概率公式与贝叶斯公式 性 质 定 义 条件 概率 不 可 能 事 件 复 合 事 件

两类现象:确定性现象;随机现象, 随机现象 在相同的条件下,并不总是出现相同的结果,其结 果是不确定的现象称为随机现象。 特点:在相同的条件下,重复进行试验或观测,其结 果不止一个,在试验之前,哪一个结果出现,人们事 先无法确定。 条件不能完全决定结果。 2024年8月27日星期二 3 目录 上页 下页 返回
2024年8月27日星期二 3 目录 上页 下页 返回 两类现象: 确定性现象; 随机现象. 特点:在相同的条件下,重复进行试验或观测,其结 果不止一个,在试验之前,哪一个结果出现,人们事 先无法确定。 条件不能完全决定结果。 在相同的条件下,并不总是出现相同的结果,其结 果是不确定的现象称为随机现象。 随机现象

随机试验 试验的条件都相同,但每一次试验的结果也可能不同, 这样的试验称为随机试验(random experiment), 随机试验常用字母E等表示 样本空间 对一个随机试验而言,其一切可能的结果组成 一个集合2,称为该试验的样本空间(sampling space).样本空间的每一个最基本的结果,即样 本空间的元素o,称为样本点(sampling point). 2024年8月27日星期二 目录 上页 下页 返回
2024年8月27日星期二 4 目录 上页 下页 返回 随机试验 试验的条件都相同,但每一次试验的结果也可能不同, 这样的试验称为随机试验(random experiment). 随机试验常用字母E等表示. 样本空间 对一个随机试验而言,其一切可能的结果组成 一个集合 ,称为该试验的样本空间(sampling space).样本空间的每一个最基本的结果,即样 本空间的元素 ,称为样本点(sampling point).

如果一个样本空间仅有有限个样本点,则称为有限 样本空间.如果有如自然数1,2,3,.那样多的点, 则称为可数的无限样本空间.如果样本点落在一个区 间内,则称为不可数的无限样本空间.当一个样本空 间是有限的或可数的无限空间时,一般称为离散样本 空间.一个不可数的无限样本空间称为非离散样本空 间 2024年8月27日星期二 5 目录 上页 下页 返回
2024年8月27日星期二 5 目录 上页 下页 返回 如果一个样本空间仅有有限个样本点,则称为有限 样本空间.如果有如自然数 1,2,3,.那样多的点, 则称为可数的无限样本空间.如果样本点落在一个区 间内,则称为不可数的无限样本空间.当一个样本空 间是有限的或可数的无限空间时,一般称为离散样本 空间.一个不可数的无限样本空间称为非离散样本空 间.

随机事件 通常,称样本空间2的一个子集A,即一 些可能结果组成的一个集合,为一个随机事件 (random event),简称事件.在每次试验中, 当且仅当子集A中的一个样本点出现时,称事 件A发生.由一个样本点构成的集合称为基本 事件(basic event);由多个样本点构成的集 合称为复合事件(composite event). 2024年8月27日星期二 6 目录 上页> 下页 。返回
2024年8月27日星期二 6 目录 上页 下页 返回 随机事件 通常,称样本空间 的一个子集 A ,即一 些可能结果组成的一个集合,为一个随机事件 (random event),简称事件.在每次试验中, 当且仅当子集 A 中的一个样本点出现时,称事 件 A 发生.由一个样本点构成的集合称为基本 事 件(basic event);由多个样本点构成的集 合称为复合事件(composite event).

样本空间Ω也是其自身的一个子集,它 包含所有的样本点,在每次试验中它总是发 生的,称2为必然事件(certain event).空 集Φ不包含任何样本点,在每次试验中都 不发生,称Φ为不可能事件(impossib1e event). 2024年8月27日星期二 7 目录○ 、上页 下页 返回
2024年8月27日星期二 7 目录 上页 下页 返回 样本空间 也是其自身的一个子集,它 包含所有的样本点,在每次试验中它总是发 生的,称 为必然事件(certain event).空 集 不包含任何样本点,在每次试验中都 不发生,称 为不可能事件(impossible event).

事件之间的关系与运算 给定一个随机试验,设2为其样本空间,事件A, B,Ak(k=1,2,3,.)都是2的子集. l、包含关系(inclusion relation) 事件A是事件B的子事件。 ◆事件A发生必然导致事件B发生 ◆事件A的样本点都是事件B的样本点 Ω ACB 记作 A B BSA 2024年8月27日星期二 8 目录○ 上页 下页 返回
2024年8月27日星期二 8 目录 上页 下页 返回 给定一个随机试验,设Ω为其样本空间,事件A, B,Ak ( k =1,2,3,. ) 都是Ω的子集. 事件之间的关系与运算 ◆ 事件A发生必然导致事件B发生 1、包含关系(inclusion relation) A B A B B A ◆ 事件A的样本点都是事件B的样本点 事件A是事件B的子事件 记作
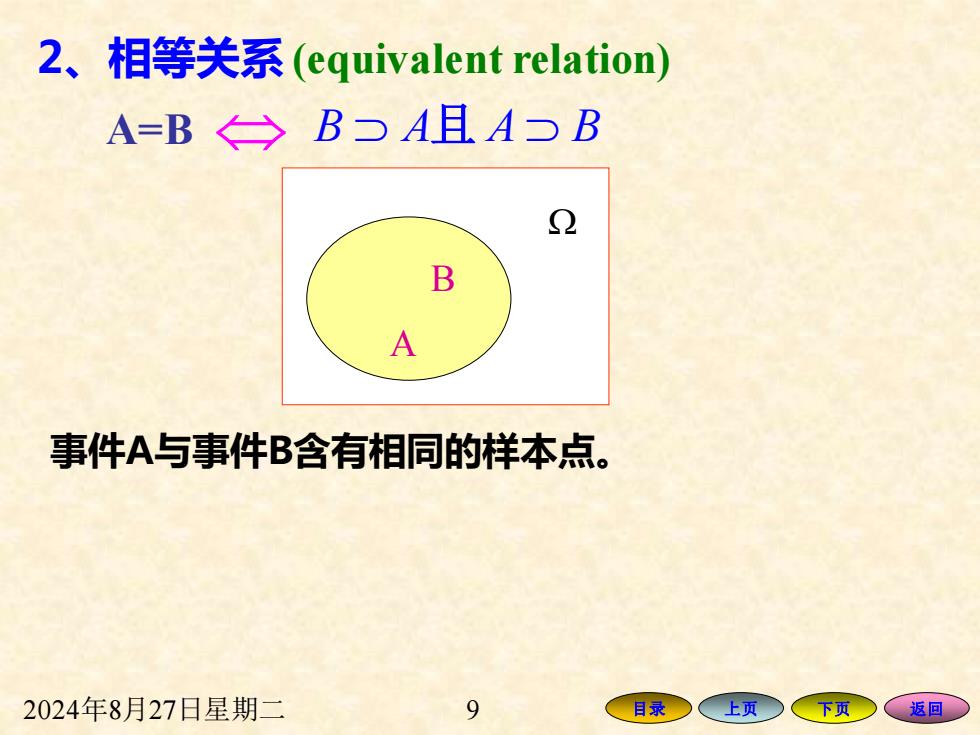
2、相等关系(equivalent relation) A=B←→B一A且A一B B 事件A与事件B含有相同的样本点。 2024年8月27日星期二 9 目录 (上页○ (下页 返回○
2024年8月27日星期二 9 目录 上页 下页 返回 A=B B A A B 且 B A 事件A与事件B含有相同的样本点。 2、相等关系 (equivalent relation)
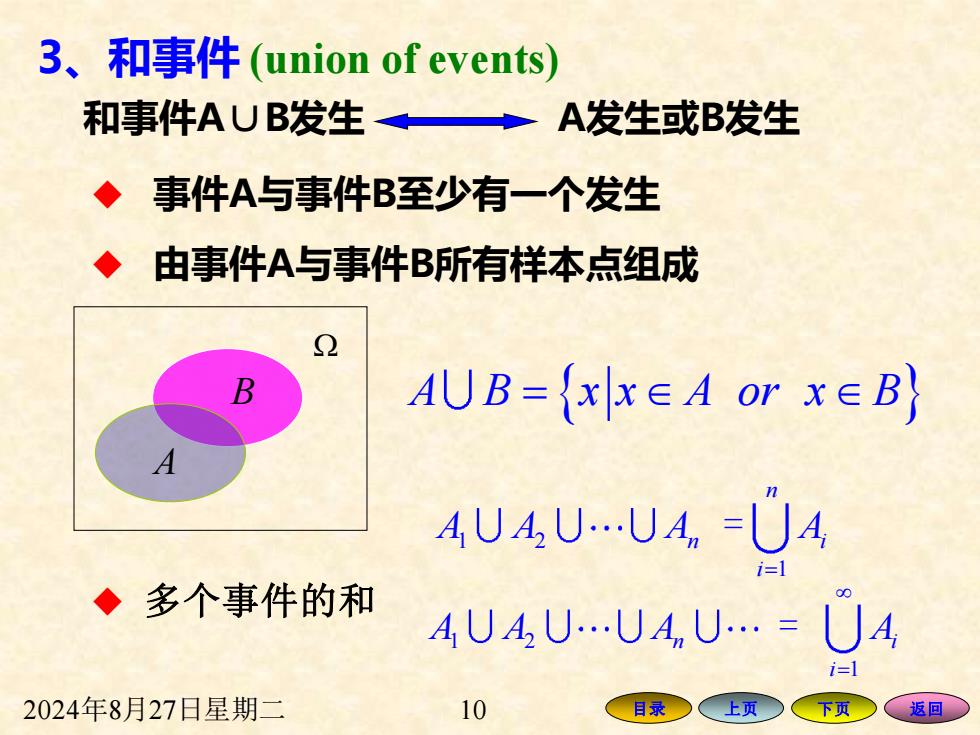
3、和事件(union of events) 和事件AUB发生→A发生或B发生 ◆事件A与事件B至少有一个发生 ◆由事件A与事件B所有样本点组成 AUB={xx∈Aorx∈B} 4UA,U.UAn=UA i= ◆多个事件的和 AUAU.UAnU.=U4 i= 2024年8月27日星期二 10 目录○ 上页○ 下页 。返回
2024年8月27日星期二 10 目录 上页 下页 返回 ◆ 事件A与事件B至少有一个发生 A B x x A or x B = A B 1 2 1 n n i i A A A A = = 1 2 1 n i i A A A A = = ◆ 由事件A与事件B所有样本点组成 ◆ 多个事件的和 和事件A∪B发生 A发生或B发生 3、和事件 (union of events)