第四节 随机变量岛数的分布 己知随机变量的分布 随机变量函数的分布 2024年8月27日星期二 1 目录○ 上页>下页 返回
2024年8月27日星期二 1 目录 上页 下页 返回 第四节 随机变量函数的分布 已知随机变量的分布 随机变量函数的分布
离散型随机变量函数的分布 例:若随机变量X的分布律为 X|-1012 1 111 Pk 188 注意 求:Y=2X+1和Z=X2的分布律 C合并) 解: y-1 13 Z 0 1。 1 1 Pk 2488 Pk 4 28 2024年8月27日星期二 2 目录○ 上页 下页 返回
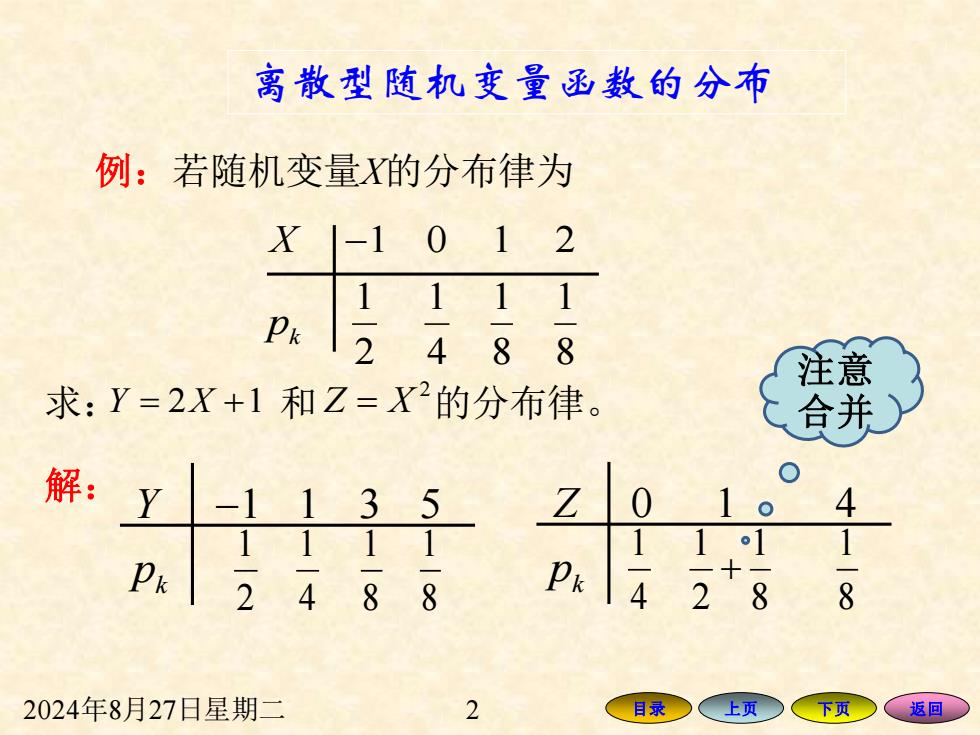
2024年8月27日星期二 2 目录 上页 下页 返回 例:若随机变量X的分布律为 1 0 1 2 1 1 1 1 2 4 8 8 − k X p 求: Y X = + 2 1 和 的分布律。 2 Z X = −1 1 3 5 k Y p 1 2 1 4 1 8 1 8 解: 0 1 4 k Z p 1 4 1 1 2 8 + 1 8 离散型随机变量函数的分布 注意 合并

连续型随机支量函数的分布 设连续型随机变量X的概率密度为f)。y=g 为一个连续函数,求随机变量=gX的概率密度。 一般方法: ()求Y的分布函数Fy) 根据分布函数的定义 F,(y) P(Y<y)=P(g(X)<y) =P(X∈{xg(x)<y) (2)对F)求导,得到fy) 解不等式转化 f(y)=F(y) 为求关于X的概率 2024年8月27日星期二 不八工火T回
2024年8月27日星期二 3 目录 上页 下页 返回 连续型随机变量函数的分布 设 连续型随机变量X 的概率密度为 f (x)。y = g(x) 为一个连续函数,求随机变量Y=g(X)的概率密度。 (1) 求Y的分布函数 FY (y) ( ) F y Y 根据分布函数的定义 P Y y ( ) = P g X y ( ( ) ) (2) 对FY (y) 求导,得到 fY (y) 一般方法: ( ) ( ) Y Y f y F y = = P X x g x y ( ( ) ) 解不等式转化 为求关于X的概率

例:若X~UU(0,1),求Y=2X+1的概率密度。 解:由题意可知,X的概率密度为 f(x)= [1,0<x<1, 10, 其它 分别记X,Y的分布函数为Fx),Fy)。 BO)-PY5-Px1-xE22 将Fy)关于y求导: 升洁卡 其它. 2024年8月27日星期二 目录○ 、上页 下页 返回
2024年8月27日星期二 4 目录 上页 下页 返回 例:若X~U(0,1),求Y=2X+1的概率密度。 解:由题意可知, X的概率密度为 1, 0 1, ( ) 0, x f x = 其它. 分别记X,Y的分布函数为FX (x) , FY (y)。 F y P Y y Y ( ) = = + P X y 2 1 1 2 − = y P X 1 ( ) 2 − = X y F 将 FY (y)关于y求导: ( ) Y f y 1 1 2 2 − − = X y y f 1 1 1 , 0 1, 2 2 0, y − = 其它. 1 , 1 3, 2 0, y = 其它

例:设正方形边长X的概率密度为 2x,0<x<1 fx(x)= 其它 求它的面积Y的概率密度。 0 解:当0时,F(y)=PY<y以=P{X2<以=0 →(y)=Fy)=0 当20时,F)=P{X2≤y=F(N)-F(←) →-阿 25×布0610cy<1 其它 0, 其它 0 2024年8月27日星期 目录 上页 下页 返回
2024年8月27日星期二 5 目录 上页 下页 返回 例: 设正方形边长 X 的概率密度为 求它的面积 Y 的概率密度。 ( ) 2 , 0 1 0, = X x x f x 其它 F y P Y y Y ( ) = 2 = P X y 1 2 0, 0 2 , 1 = y y y 其它 1, 0 1 0, = y 其它 解:当 y<0时, = 0 = = ( ) ( ) 0 Y Y f y F y 当 y≥0时, 2 F y P X y Y ( ) = = − − ( ) ( ) F y F y X X ( ) ( ) ( ) 1 1 2 2 = − − − Y X X f y f y f y y y

例:若连续型随机变量X的概率密度为fx)。 求Y=X的概率密度。 解:当 (上页 下页 返回
2024年8月27日星期二 6 目录 上页 下页 返回 例:若连续型随机变量X的概率密度为fX (x) 。 求 Y X = 的概率密度 。 解:当 y<0时, F y P Y y P X y Y ( ) 0 = = = ( ) ( ) 0 = = Y Y 所以 f y F y 当 y≥0时, F y P Y y Y ( ) = = P X y = − P y X y = − − ( ) ( ) F y F y X X 将 FY (y)关于y求导: f y f y f y Y X X ( ) ( ) ( ) = + − ( ) ( ), 0, ( ) 0, 0. + − = X X Y f y f y y f y y 综上

例:设圆面积X~U[O,π],求圆半径Y的概率密度. 解:由翅设,r-厚内层到 0, 其它 =P对WN 当y<0时,F,(y)=0→(y)=0 当20时,F(y)=P{X<πy}=Fx(πy) 所以人(y)=∫x(πy2)2πy x2π,0≤zy2≤π_∫2y, 0≤y≤1 =π 0, 其它 0, 其它 2024年8月27日星期二 7 目录 上页 下页 返回
2024年8月27日星期二 7 目录 上页 下页 返回 例: 设圆面积 X U~ 0, , 求圆半径 Y 的概率密度. 解:由题设, ( ) 1 , 0, , 0, = = X X x Y f x 其它 所以 ( ) ( ) 2 2 Y X f y f y y = F y P Y y Y ( ) = X P y = ( ) 0 Y = f y ( ) 2 = F y X 1 2 2 , 0 0, = y y 其它 2 , 0 1 0, = y y 其它 当 y<0时, ( ) 2 当 y≥0时, F y P X y Y = ( ) = 0 F y Y

定理:若随机变量X和随机变量Y=)的密度函数分 别为fxc),fyy),当gc)是严格单调函数,则 f(y)=fx[(G(y川G'(y) 其中x=G(y)为y=g(x)的反函数 2024年8月27日星期二 8 目录○ (上页下页 返回
2024年8月27日星期二 8 目录 上页 下页 返回 ( ) [( ( )] ( ) Y X f y f G = y G y 定理: 若随机变量X和随机变量Y=g(X)的密度函数分 别为 f X (x), f Y (y), 当 g(x) 是严格单调函数,则 其中 为 的反函数 x G y y g x = = ( ) ( )

例:若X~N(4,σ2),求Y=aX+b(a≠0)的概率密度。 解:随机变量X的概率密度为 1 (x-u)2 f(x)= -e 2.2 √2元0 ,-00 下页 返回
2024年8月27日星期二 9 目录 上页 下页 返回 例:若 X N( , ) 2 ,求Y=aX+b(a≠0)的概率密度 。 解:随机变量X的概率密度为 2 2 ( ) 2 1 ( ) e , , 2 x f x x − − = − + 由 y g x ax b = = + ( ) ( ) − = = y b x G y a 可得: 由定理可得Y=aX+b(a≠0)的概率密度为 1 ( ) , − = − + Y X y b f y f y a a 即 2 2 ( ) 2 1 1 ( ) e 2π − − − = y b a Y f y a 2 2 [ ( )] 1 2( ) e , 2π − + − = − + y b a a y a 即 2 Y N a b a ~ ( , ( ) ) +

定理:正态分布的线性函数仍服从正态分布. 设X~N(4,o2),Y=aX+b(a≠0),则 Y~N(au+b,(ao)2) 推论 若xu则。w0) 正态分布 的标准化 2024年8月27日星期二 10 目录 返回○
2024年8月27日星期二 10 目录 上页 下页 返回 2 2 ~ ( , ), ( 0), ~ ( , ( ) ) + X = + Y N a N Y aX b b a a 设 则 2 ~ ( , ), ~ (0,1) X − X N N 若 则 推论: 定理: 正态分布的线性函数仍服从正态分布. 正态分布 的标准化