
第一章随机事件和糯年 §1.1 随机事件 §1.2 概率的定义 §1.3 条件概率、全概率公式和 贝叶斯公式 §1.4 事件的独立性 §1.5伯努利(Bernoulli)概型 2024年8月27日星期二 2 目录○ 上页 下页 返回
2024年8月27日星期二 2 目录 上页 下页 返回 第一章 随机事件和概率 §1.1 随机事件 §1.2 概率的定义 §1.3 条件概率、全概率公式和 贝叶斯公式 §1.4 事件的独立性 §1.5 伯努利(Bernoulli)概型

§1.2撬李的定义 一、概率的统计定义 二、概率的公理化定义及概率的性质 三、概率的古典定义 四、概率的几何定义 2024年8月27日星期二 3 目录○ 上页>下页 返回
2024年8月27日星期二 3 目录 上页 下页 返回 二、概率的公理化定义及概率的性质 一、概率的统计定义 三、概率的古典定义 §1.2 概率的定义 四、概率的几何定义

一、概率的统计定义 1、频率及频率的性质 定义1在相同的条件下,重复进行了n次试验,事件A 发生的次数n,称为事件A发生的频数,比值”4称为事 件A发生的频率(frequency).,记为f,(A). 性质:(1)非负性:对任意A,有f,(A)≥0; (2)规范性:f(2)=1; (3)有限可加性: 04)-2(4 2024年8月27日星期二 目录 、上页 下页 返回
2024年8月27日星期二 4 目录 上页 下页 返回 一、概率的统计定义 1、频率及频率的性质 定义 1 在相同的条件下,重复进行了 n 次试验,事件 A 发生的次数 A n 称为事件 A 发生的频 数,比值 A n n 称为事 件 A 发生的频率(frequency),记为 ( ) n f A . 性质: (1) 非负性:对任意 A ,有 ( ) 0 n f A ; (2) 规范性: ( ) 1 n f = ; (3) 有限可加性: ( ) 1 1 . k k n i n i i i f A f A = = =
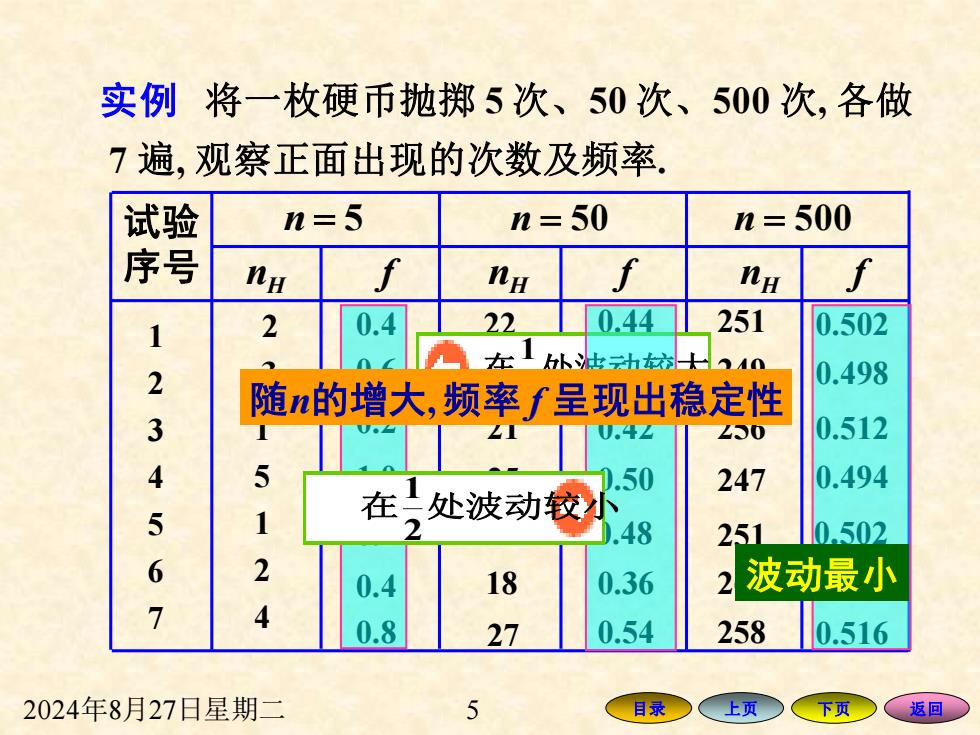
实例将一枚硬币抛掷5次、50次、500次,各做 7遍,观察正面出现的次数及频率. 试验 n=5 n=50 n=500 序号 ne na f H f 2 0.4 2 0.44 251 0.502 在1池动士40 2 0.498 随n的增大,频率f呈现出稳定性 3 U.44 250 0.512 4 .50 247 0.494 5 在一处波动较 .48 251 0.502 6 0.4 18 0.36 2波动最小 0.8 27 0.54 258 0.516 2024年8月27日星期二 5 目录 、上页> 下页 返回
2024年8月27日星期二 5 目录 上页 下页 返回 试验 序号 n = 5 nH f 1 2 3 4 5 6 7 2 3 1 5 1 2 4 nH f n = 50 22 25 21 25 24 18 27 nH n = 500 251 249 256 247 251 262 258 0.4 0.6 0.2 1.0 0.2 0.4 0.8 0.44 0.50 0.42 0.48 0.36 0.54 f 0.502 0.498 0.512 0.494 0.524 0.516 0.50 0.502 实例 将一枚硬币抛掷 5 次、50 次、500 次, 各做 7 遍, 观察正面出现的次数及频率. 在 处波动较大 2 1 波动最小 随n的增大, 频率 f 呈现出稳定性 在 处波动较小 2 1

从上述数据可得 (1)频率有随机波动性即对于同样的n,所得的 f不一定相同; (2)抛硬币次数n较小时,频率f的随机波动幅 度较大,但随n的增大,频率f呈现出稳定性.即 当n逐渐增大时频率f总是在0.5附近摆动,且 逐渐稳定于0.5. 2024年8月27日星期二 6 目录 、上页 下页 返回○
2024年8月27日星期二 6 目录 上页 下页 返回 从上述数据可得 (2) 抛硬币次数 n 较小时, 频率 f 的随机波动幅 度较大, 但随 n 的增大 , 频率 f 呈现出稳定性.即 当 n 逐渐增大时频率 f 总是在 0.5 附近摆动, 且 逐渐稳定于 0.5. (1) 频率有随机波动性,即对于同样的 n, 所得的 f 不一定相同;
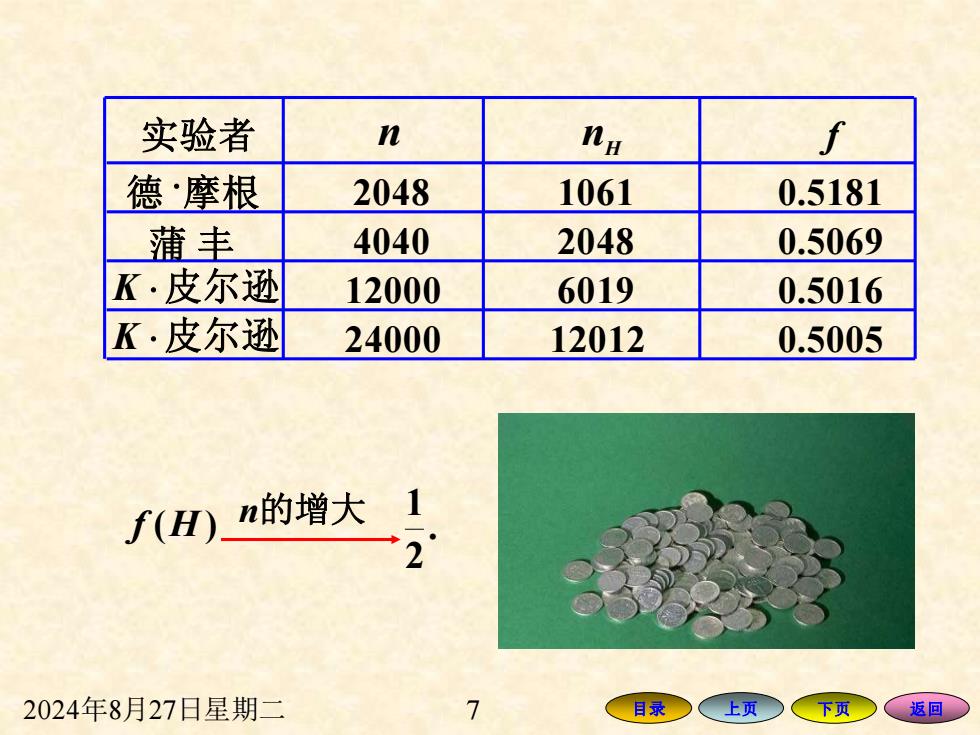
实验者 n na r 德·摩根 2048 1061 0.5181 蒲丰 4040 2048 0.5069 K·皮尔逊 12000 6019 0.5016 K·皮尔逊 24000 12012 0.5005 f(H) n的增大1 2 2024年8月27日星期二 7 目录上页○下页○返回
2024年8月27日星期二 7 目录 上页 下页 返回 实验者 德 摩根 蒲 丰 n nH f K 皮尔逊 K 皮尔逊 2048 1061 0.5181 4040 2048 0.5069 12000 6019 0.5016 24000 12012 0.5005 f (H) n的增大 . 2 1

重要结论 频率当n较小时波动幅度比较大,当n逐渐增 大时,频率趋于稳定值,这个稳定值从本质上反映 了事件在试验中出现可能性的大小.它就是事件的 概率. 2024年8月27日星期二 8 目录> 、上页 下页 返回
2024年8月27日星期二 8 目录 上页 下页 返回 重要结论 频率当 n 较小时波动幅度比较大,当 n 逐渐增 大时 , 频率趋于稳定值,这个稳定值从本质上反映 了事件在试验中出现可能性的大小.它就是事件的 概率.

概率的统计定义 在相同的条件下,独立重复作n次试验,当试验 次数n很大时,如果某事件A发生的频率f,()稳定 地在[0,1]上的某一数值p附近摆动,而且一般来说 随着试验次数的增多,这种摆动的幅度会越来越小, 则称数值p为事件A发生的概率(probability),记 为P(A)=p. 2024年8月27日星期二 9 目录○ 上页>下页 返回
2024年8月27日星期二 9 目录 上页 下页 返回 概率的统计定义 在相同的条件下,独立重复作 n 次试验,当试验 次数 n 很大时,如果某事件 A 发生的频率 ( ) n f A 稳定 地在[0,1]上的某一数值 p 附近摆动,而且一般来说 随着试验次数的增多,这种摆动的幅度会越来越小, 则称数值 p 为事件 A 发生的概率(probability),记 为 P A p ( ) = .

思考 医生在检查完病人的时候摇摇头:“你的 病很重,在十个得这种病的人中只有一个能救活 当病人被这个消息吓得够呛时,医生继续说: “但你是幸运的.因为你找到了我,我已经看过 九个病人了,他们都死于此病” 医生的说法对吗? 2024年8月27日星期二 10 目录>上页 下页 、返回
2024年8月27日星期二 10 目录 上页 下页 返回 医生在检查完病人的时候摇摇头:“你的 病很重,在十个得这种病的人中只有一个能救活 .” 当病人被这个消息吓得够呛时,医生继续说: “但你是幸运的.因为你找到了我,我已经看过 九个病人了,他们都死于此病.” 医生的说法对吗? 思考

二、概率的公理化定义及概率的性质 1933年,苏联数学家柯尔莫哥洛夫提出了概 率论的公理化结构,给出了概率的严格定义,使 概率论有了迅速的发展 柯尔莫哥洛夫资料 2024年8月27日星期二 11 目录 上页> 下页 返回
2024年8月27日星期二 11 目录 上页 下页 返回 二、概率的公理化定义及概率的性质 1933年 ,苏联数学家柯尔莫哥洛夫提出了概 率论的公理化结构 ,给出了概率的严格定义 ,使 概率论有了迅速的发展. 柯尔莫哥洛夫资料