
概華伦与款程统外 第二节方差 一、随机变量方差的概念及性质 二、重要概率分布的方差 三、例题讲解 四、小结
一、随机变量方差的概念及性质 三、例题讲解 二、重要概率分布的方差 四、小结 第二节 方 差
概车纶与款理统外 一、随机变量方差的概念及性质 1.概念的引入 方差是一个常用来体现随机变量取值分散程 度的量. 实例有两批灯泡,其平均寿命都是E)=1000小时. 0 1000 ● 1000
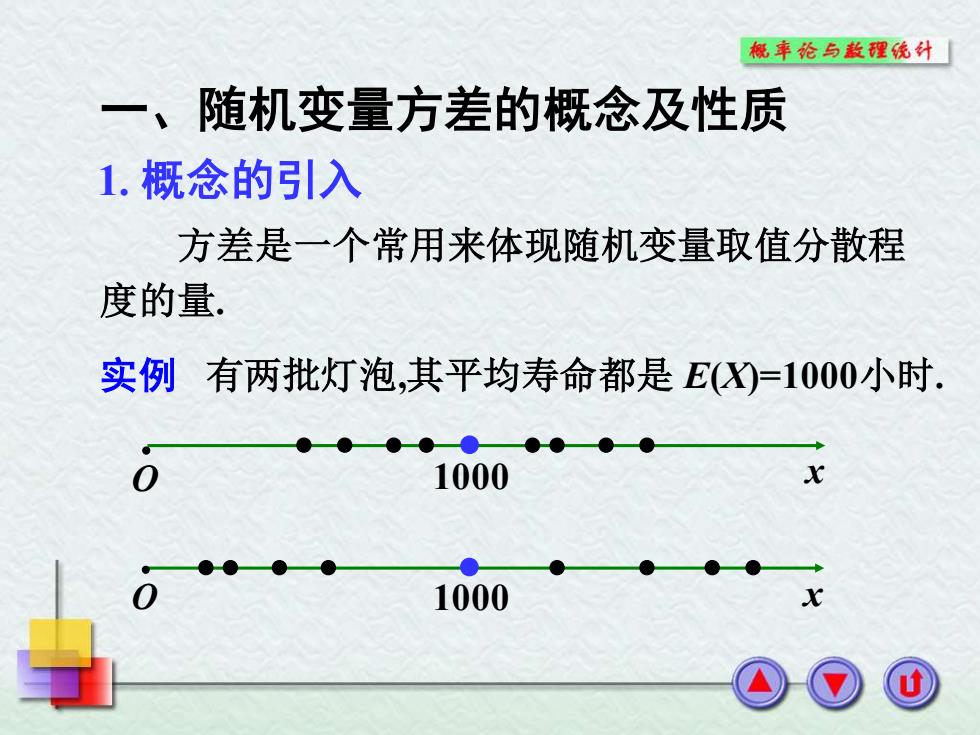
1. 概念的引入 方差是一个常用来体现随机变量取值分散程 度的量. 实例 有两批灯泡,其平均寿命都是 E(X)=1000小时. • O x • • • • • • • • • O x • • • • • • • • • 1000 • 1000 一、随机变量方差的概念及性质

概華论与款醒硫外「 2.方差的定义 设X是一个随机变量若E{[X-E(X)}存在, 则称E{X-E(X)2}为X的方差,记为D(X)或 Var(X),即. D(X)=Var(X)=EX-E(X). 称√D(X)为标准差或均方差,记为σ(X)
( ) , ( ). ( ) Var( ) {[ ( )] }. Var( ), {[ ( ) ] } , ( ) , {[ ( )] } , 2 2 2 D X σ X D X X E X E X X E X E X X D X X E X E X 称 为标准差或均方差 记 为 即 则 称 为 的方差 记 为 或 设 是一个随机变量若 存 在 = = − − − 2. 方差的定义

概车纶与款理统外 3.方差的意义 方差是一个常用来体现随机变量X取值分 散程度的量.如果D)值大,表示X取值分散 程度大,E)的代表性差;而如果D)值小,则 表示X的取值比较集中,以E)作为随机变量 的代表性好
方差是一个常用来体现随机变量 X 取值分 散程度的量. 如果 D(X) 值大, 表示 X 取值分散 程度大, E(X) 的代表性差; 而如果 D(X) 值小, 则 表示X 的取值比较集中, 以 E(X) 作为随机变量 的代表性好. 3. 方差的意义

概華论与款醒硫外 4.随机变量方差的计算 ()利用定义计算 离散型随机变量的方差 十00 D(X)=∑Ix-E(X)rp, k= 其中P{X=x}=Pk,k=1,2,.是X的分布律 连续型随机变量的方差 D(X)=x-E(X)If(x)d.x, 其中f(x)为X的概率密度
离散型随机变量的方差 ( ) [ ( )] , 1 2 k k D X xk E X p + = = − 连续型随机变量的方差 ( ) [ ( )] ( )d , 2 D X x E X f x x + − = − 4. 随机变量方差的计算 (1) 利用定义计算 其中 f (x)为X的概率密度. 其中P{X x } p , k 1,2, 是 X 的分布律. = k = k =

概车纶与款理统外 (2)利用公式计算 D(X)=E(X2)-E(X)P. 证明D(X)=E{X-E(X)) =E{X2-2XE(X)+[E(X)2} =E(X2)-2E(X)E(X)+[E(X)I2 =E(X2)-[E(X)2 =E(X2)-E2(X)
( ) ( ) [ ( )] . 2 2 D X = E X − E X 证明 ( ) {[ ( )] } 2 D X = E X − E X { 2 ( ) [ ( )] } 2 2 = E X − XE X + E X 2 2 = E(X ) − 2E(X)E(X) + [E(X)] 2 2 = E(X ) − [E(X)] (2) 利用公式计算 ( ) ( ). 2 2 = E X − E X

概華论与款醒硫外「 5.方差的性质 (1)设C是常数,则有D(C)=0. 证明D(C)=E(C2)-[E(C)=C2-C2=0. (2)设X是一个随机变量,C是常数,则有 D(CX)=CD(X). 证明D(CX)=E{ICX-E(CX)} =C2EX-E( =CD(X)
证明 2 2 D(C) = E(C ) − [E(C)] 5. 方差的性质 (1) 设 C 是常数, 则有 D(C) = 0. 2 2 = C −C = 0. (2) 设 X 是一个随机变量, C 是常数, 则有 ( ) ( ). 2 D CX = C D X 证明 D(CX ) {[ ( )] } 2 2 = C E X − E X ( ). 2 = C D X {[ ( )] } 2 = E CX − E CX

概车纶与款理统外 (3)设X,Y相互独立,D),D()存在,则 D(X±Y)=D(X)+D(Y): 证明 D(X±Y)=EI(X±Y)-E(X±Y)I} =EX-E(X)】±Y-E(Y)}2 EIX-E(X)2+E[Y-E(Y) ±2E{[X-E(X)川Y-E(Y)} =D(X)+D(Y)
D(X Y ) = D(X) + D(Y ). (3) 设 X, Y 相互独立, D(X), D(Y) 存在, 则 证明 ( ) {[( ) ( )] } 2 D X Y = E X Y − E X Y 2 = E{[X − E(X)] [Y − E(Y )]} 2 {[ ( )][ ( )]} [ ( )] [ ( )] 2 2 E X E X Y E Y E X E X E Y E Y − − = − + − = D(X) + D(Y )

概華论与款程统外 推广若X1,X2,.,Xn相互独立,则有 D(X±X2±.±Xn)=D(X)+D(X2)+.+D(Xn) (4)D(X)=0的充要条件是X以概率1取常数 C,即 P{X=C}=1
推广 ( ) ( ) ( ) ( ). D X1 X2 Xn = D X1 + D X2 ++ D Xn 若 X1 ,X2 , ,Xn 相互独立,则有 即 的充要条件是 以概率 取常数 , (4) ( ) 0 1 C D X = X P{X = C} = 1

概车纶与款理统外 分 布 参数 数学期望 方差 两点分布 00 2 兄 均匀分布 a0 0 02 正态分布 4,o>0 u G2
0 p 1 p p(1− p) 0 1 1, p n np np(1 − p) 0 a b (a + b) 2 ( ) 12 2 b − a θ 0 θ 2 θ 分 布 参数 数学期望 方差 两点分布 二项分布 泊松分布 均匀分布 指数分布 正态分布 μ,σ 0 μ 2 σ