《概率论与数理统计》课程教学资源（PPT课件）第一章 概率论的基本概念 第四节 等可能概型（古典概型）

概车纶与款理统外「 第四节等可能概型（古典概型） 一、等可能概型 二、典型例题 三、几何概率 四、小结

一、等可能概型 二、典型例题 三、几何概率 四、小结 第四节 等可能概型(古典概型)

概華论与款程统外 一、等可能概型（古典概型 1.定义 (①)试验的样本空间只包含有限个元素； (2)试验中每个基本事件姓的可能性相同 具有以上两个特点的试验称为等可能概型或 古典概型

. (2) . (1) ; 古典概型 具有以上两个特点的试验称为等可能概型或 试验中每个基本事件发生的可能性相同 试验的样本空间只包含有限个元素 1. 定义 一、等可能概型(古典概型)

概车纶与款理统外 2.古典概型中事件概率的计算公式 设试验E的样本空间由n个样本点构成，A 为E的任意一个事件，且包含m个样本点，则事 件A出现的概率记为： m A所包含样本点的个数 P(A)= n 样本点总数 称此为概率的古典定义

设试验 E 的样本空间由n 个样本点构成， A 为 E 的任意一个事件，且包含 m 个样本点，则事 件 A 出现的概率记为: 2. 古典概型中事件概率的计算公式 ( ) . 样本点总数 A 所包含样本点的个数 n m P A = = 称此为概率的古典定义

概華伦与款程统外 3.古典概型的基本模型摸球模型 ()无放回地摸球 问题1设袋中有4只白球和2只黑球，现从袋中无 放回地依次摸出2只球，求这2只球都是白球的概率 解设A=摸得2只球都是白球}， 6 基本事件总数为 2 A所包含基本事件的个数为 2 故P(A)

3. 古典概型的基本模型:摸球模型 (1) 无放回地摸球 问题1 设袋中有4 只白球和 2只黑球, 现从袋中无 放回地依次摸出2只球,求这2只球都是白球的概率. 解 设 A = {摸得 2 只球都是白球}, 基本事件总数为 , 2 6       A 所包含基本事件的个数为 , 2 4                   = 2 6 2 4 故 P(A) . 5 2 =

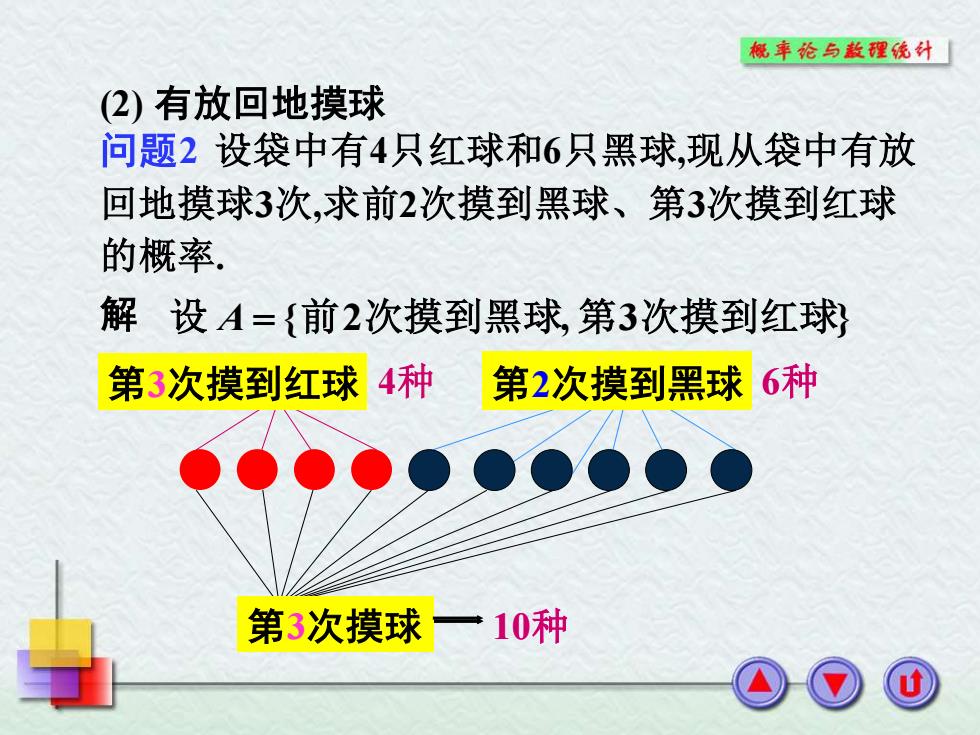
概车纶与款理统外 (2)有放回地摸球 问题2设袋中有4只红球和6只黑球，现从袋中有放 回地摸球3次，求前2次摸到黑球、第3次摸到红球 的概率。 解设A={前2次摸到黑球第3次摸到红球) 第3次摸到红球4种 第2次摸到黑球6种 ●●q 第3次摸球一10种

(2) 有放回地摸球 问题2 设袋中有4只红球和6只黑球,现从袋中有放 回地摸球3次,求前2次摸到黑球、第3次摸到红球 的概率. 解 设 A = {前2次摸到黑球, 第3次摸到红球} 第123次摸球 10种 第3次摸到红球 4种 第12次摸到黑球黑 6种

概率伦与款理统外 基本事件总数为10×10×10=103， A所包含基本事件的个数为6×6×4， 故P(A)= 6×6×4 =0.144. 103 课堂练习 1°电话号码问题在7位数的电话号码中，第一位 不能为0，求数字0出现3次的概率. 2骰子问题 掷3颗均匀骰子，求点数之和为4的 概率. (答案：p=3/63)

基本事件总数为 10 10 10 10 , 3   = A 所包含基本事件的个数为 664, 3 10 6 6 4 ( )   故 P A = = 0.144. 课堂练习 1 o 电话号码问题 在7位数的电话号码中,第一位 不能为0，求数字0出现3次的概率. 2 o 骰子问题 掷3颗均匀骰子,求点数之和为4的 概率. 1 9 9 10 ) 3 6 1 9 ( : 3 3 6               答案 p = ( : 3 6 ) 3 答案 p =

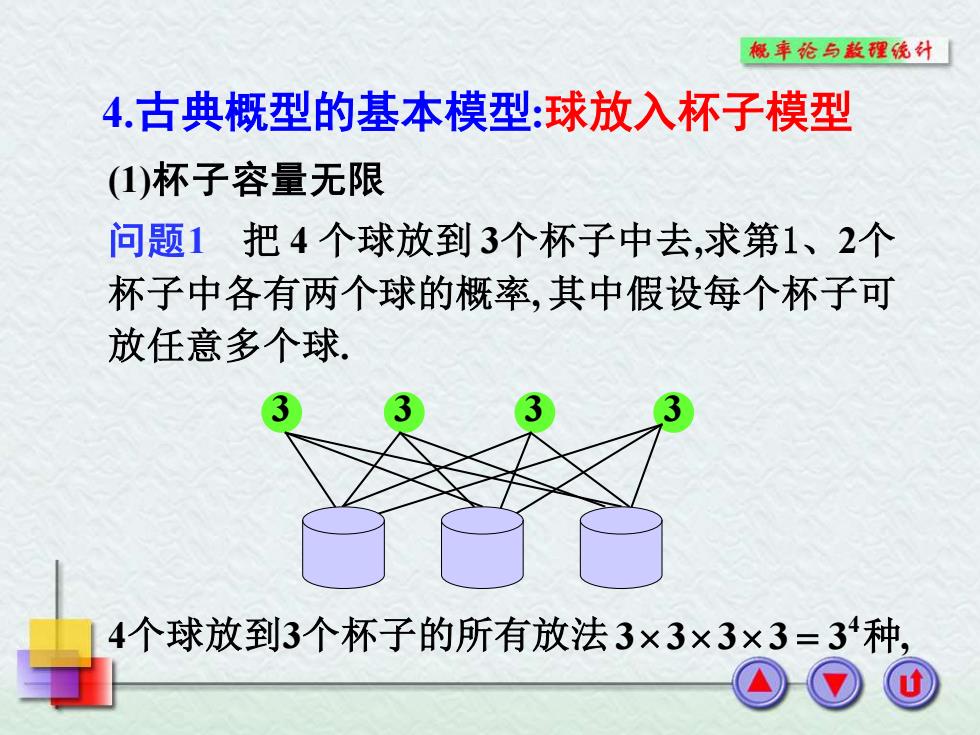
概车纶与款理统外「 4.古典概型的基本模型：球放入杯子模型 ()杯子容量无限 问题1把4个球放到3个杯子中去，求第1、2个 杯子中各有两个球的概率，其中假设每个杯子可 放任意多个球 4个球放到3个杯子的所有放法3×3×3×3=34种

4.古典概型的基本模型:球放入杯子模型 (1)杯子容量无限 问题1 把 4 个球放到 3个杯子中去,求第1、2个 杯子中各有两个球的概率, 其中假设每个杯子可 放任意多个球. 3 3 3 3 4个球放到3个杯子的所有放法 3 3 3 3 3 ,    = 4种

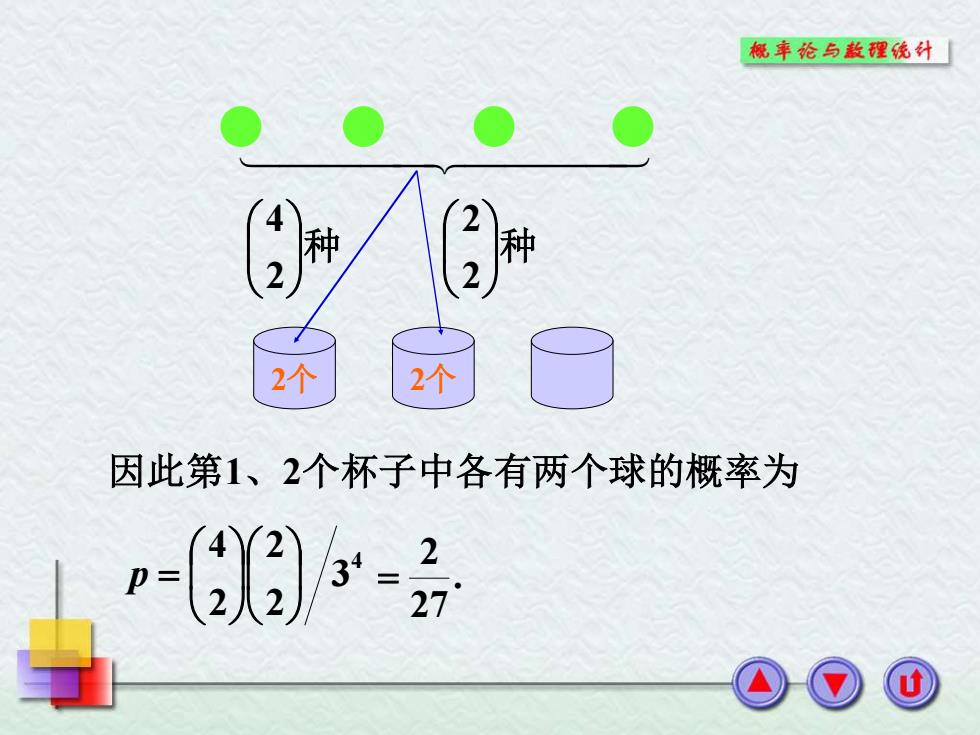
概率伦与款程统外 种 2个 2个 因此第1、2个杯子中各有两个球的概率为 =)3-号

 2个 种      2 4 2个 种      2 2 因此第1、2个杯子中各有两个球的概率为 4 3 2 2 2 4             p = . 27 2 =

概车纶与款理统外 (2)每个杯子只能放一个球 问题2把4个球放到10个杯子中去，每个杯子只能 放一个球，求第1至第4个杯子各放一个球的概率 解第1至第4个杯子各放一个球的概率为 p 4×3×2×1 Pio 10×9×8×7 1 210

(2) 每个杯子只能放一个球 问题2 把4个球放到10个杯子中去,每个杯子只能 放一个球, 求第1 至第4个杯子各放一个球的概率. 解 第1至第4个杯子各放一个球的概率为 4 10 4 4 p p p = 10 9 8 7 4 3 2 1       = . 210 1 =

概華论与款醒硫外 课堂练习 1°分房问题将张三、李四、王五3人等可能地 分配到3间房中去，试求每个房间恰有1人的概率. (答案：2/9) 2°生日问题某班有20个学生都 是同一年出生的，求有10个学生生 日是1月1日，另外10个学生生日是 12月31日的概率. (答案：p= 2010 36520)

2 o 生日问题 某班有20个学生都 是同一年出生的,求有10个学生生 日是1月1日,另外10个学生生日是 12月31日的概率. (答案 : 2 9) 365 ) 10 10 10 20 ( : 20             答案 p = 课堂练习 1 o 分房问题 将张三、李四、王五3人等可能地 分配到3 间房中去,试求每个房间恰有1人的概率