
概车纶与款理统外 第二节 离散型随机变量 及其分布律 一、离散型随机变量的分布律 二、常见离散型随机变量的概率分布 三、小结
一、离散型随机变量的分布律 二、常见离散型随机变量的概率分布 三、小结 第二节 离散型随机变量 及其分布律

概華论与款醒硫外 一、离散型随机变量的分布律 定义设离散型随机变量X所有可能取的值为 xx(k=1,2,),X取各个可能值的概率,即事件 {X=X}的概率,为 P{X=X}=Pk,k=1,2,. 称此为离散型随机变量X的分布律。 说明 (1)pk≥0,k=1,2,. (2)p.=1
说明 (1) p 0, k = 1,2, ; k (2) 1. 1 = k= pk . { } , 1,2, . { } , ( 1,2, ), , 称此为离散型随机变量 的分布律 的概率 为 取各个可能值的概率 即事件 设离散型随机变量 所有可能取的值为 X P X x p k X x x k X X k k k k = = = = = 一、离散型随机变量的分布律 定义
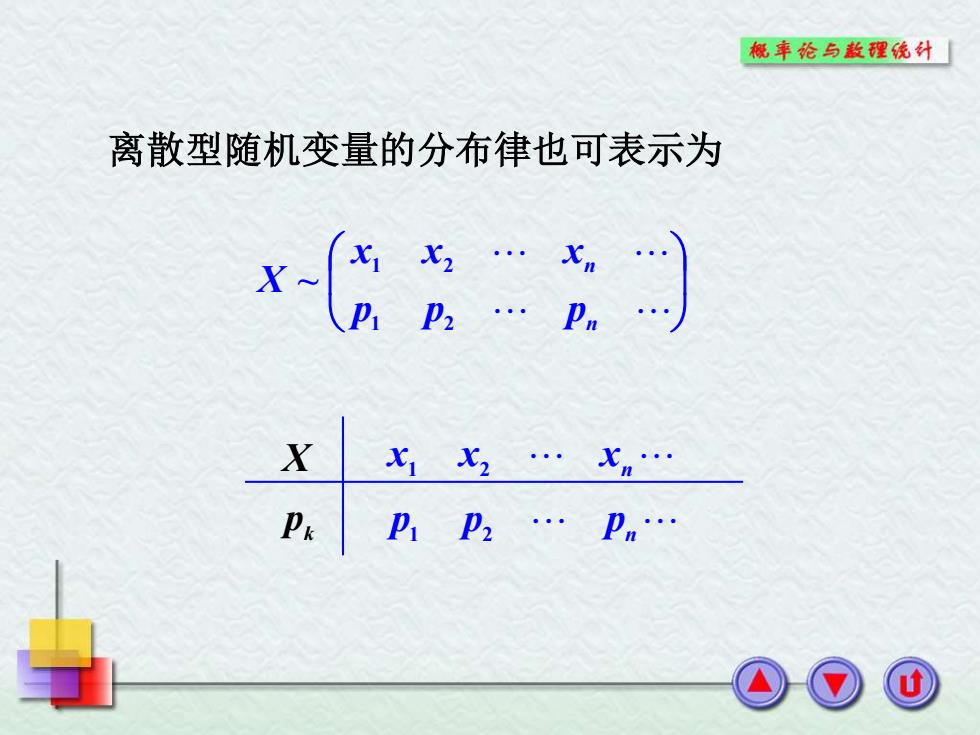
概车纶与款理统外 离散型随机变量的分布律也可表示为 X~ PkpP2.Pn
离散型随机变量的分布律也可表示为 n n p p p x x x X 1 2 1 2 ~ X pk x1 x2 xn p1 p2 pn

概率论与款理统针「 例1设一汽车在开往目的地的道路上需经过四 组信号灯,每组信号灯以1/2的概率允许或禁止汽 车通过.以X表示汽车首次停下时,它已通过的信 号灯的组数(设各组信号灯的工作是相互独立的), 求X的分布律. 解 设p为每组信号灯禁止汽通过的概率则有 X 0 1 2 3 pp(1-p)p1-p)2p(1-p)3p(1-p)
. ( ), . , , 1 2 求 的分布律 号灯的组数 设各组信号灯的工作是相互独立的 车通过 以 表示汽车首次停下时 它已通过的信 组信号灯 每组信号灯以 的概率允许或禁止汽 设一汽车在开往目的地的道路上需经过四 X X 解设 p为每组信号灯禁止汽车通过的概率, 则有 p k X 0 1 2 3 4 p (1 − p) p p p2 (1 − ) p p3 (1 − ) 4 (1 − p) 例 1

概车纶与款理统外 将P代入府 1 2 3 4 0.5 0.25 0.125 0.0625 0.0625
将 代入得 2 1 p = X pk 0 1 2 3 4 0.5 0.25 0.125 0.0625 0.0625

概華论与款醒硫外「 二、常见离散型随机变量的概率分布 1.两点分布 设随机变量X只可能取0与1两个值,它的分 布律为 则称X服从(0一1)分布或两点分布
二、常见离散型随机变量的概率分布 设随机变量 X 只可能取0与1两个值 , 它的分 布律为 X k p 0 1− p 1 p 则称 X 服从 (0—1) 分布或两点分布. 1.两点分布

概车纶与款理统外 实例1“抛硬币”试验,观察正、反两面情 况. 0,当e=正面, X=xe)F1,当e=反面。 随机变量X服从(0一1)分布. 其分布律为
实例1 “抛硬币”试验,观察正、反两面情 况. 随机变量 X 服从 (0—1) 分布. 1, X = X(e) = 0, 当e = 正面, 当e = 反面. X pk 0 1 2 1 2 其分布律为 1

概華论与款醒硫外 实例2200件产品中,有190件合格品,10件不合格 品,现从中随机抽取一件,那末,若规定 取得不合格品, 0,取得合格品. X 0 1 190 10 200 200 则随机变量X服从(0一1)分布
实例2 200件产品中,有190件合格品,10件不合格 品,现从中随机抽取一件,那末,若规定 = 0, 1, X 取得不合格品, 取得合格品. 则随机变量 X 服从(0 —1)分布. X k p 0 1 200 190 200 10

概车纶与款理统外 说明 两点分布是最简单的一种分布,任何一个只有 两种可能结果的随机现象,比如新生婴儿是男还是 女、明天是否下雨、种籽是否发芽等,都属于两点 分布. 两点分布随机数演示
两点分布是最简单的一种分布,任何一个只有 两种可能结果的随机现象, 比如新生婴儿是男还是 女、明天是否下雨、种籽是否发芽等, 都属于两点 分布. 说明 两点分布随机数演示
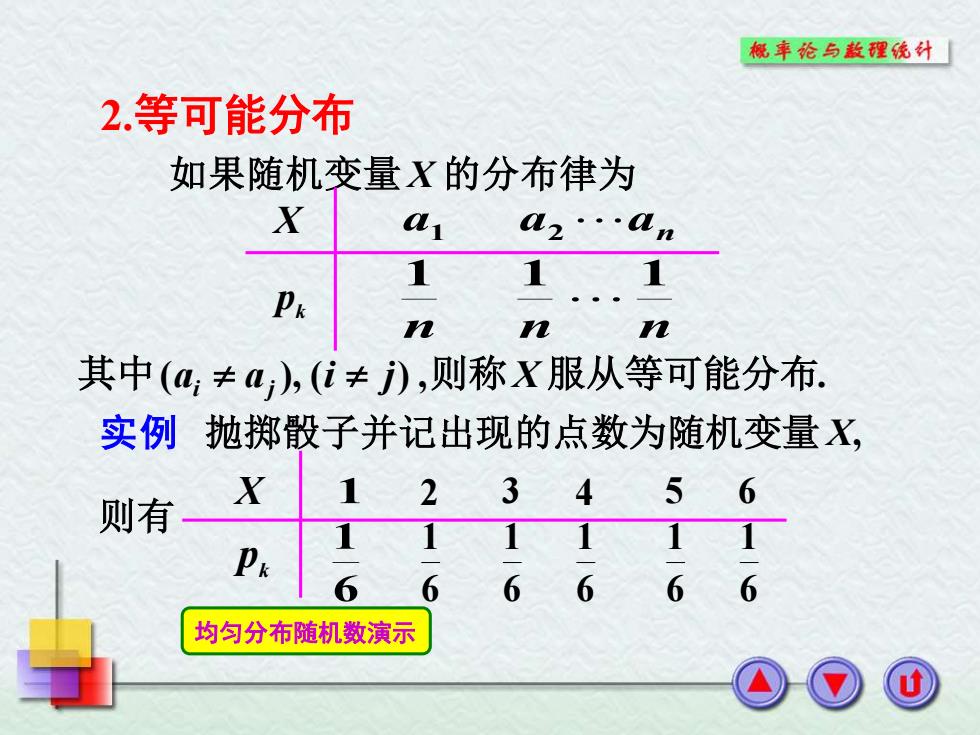
概率伦与款理统外 2.等可能分布 如果随机变量X的分布律为 X al a2···%, 1 1 n n 其中(a,≠a),(i≠),则称X服从等可能分布. 实例抛掷骰子并记出现的点数为随机变量X, 则有 X 123456 11 111 Pe 6 66 66 均匀分布随机数演示
2.等可能分布 如果随机变量 X 的分布律为 实例 抛掷骰子并记出现的点数为随机变量 X, X k p 1 6 1 2 3 4 5 6 6 1 6 1 6 1 6 1 6 1 则有 其中(a a ), (i j) ,则称X 服从等可能分布. i j X pk a1 a2 an n n n 1 1 1 均匀分布随机数演示