《概率论与数理统计》课程教学资源（PPT课件）第二章 随机变量及其分布 第四节 连续型随机变量及其概率密度

概華纶与款程统外 第四节 连续型随机变量及其概率 密度 一、概率密度的概念与性质 二、常见连续型随机变量的分布 三、小结

一、概率密度的概念与性质 二、常见连续型随机变量的分布 三、小结 第四节 连续型随机变量及其概率 密度

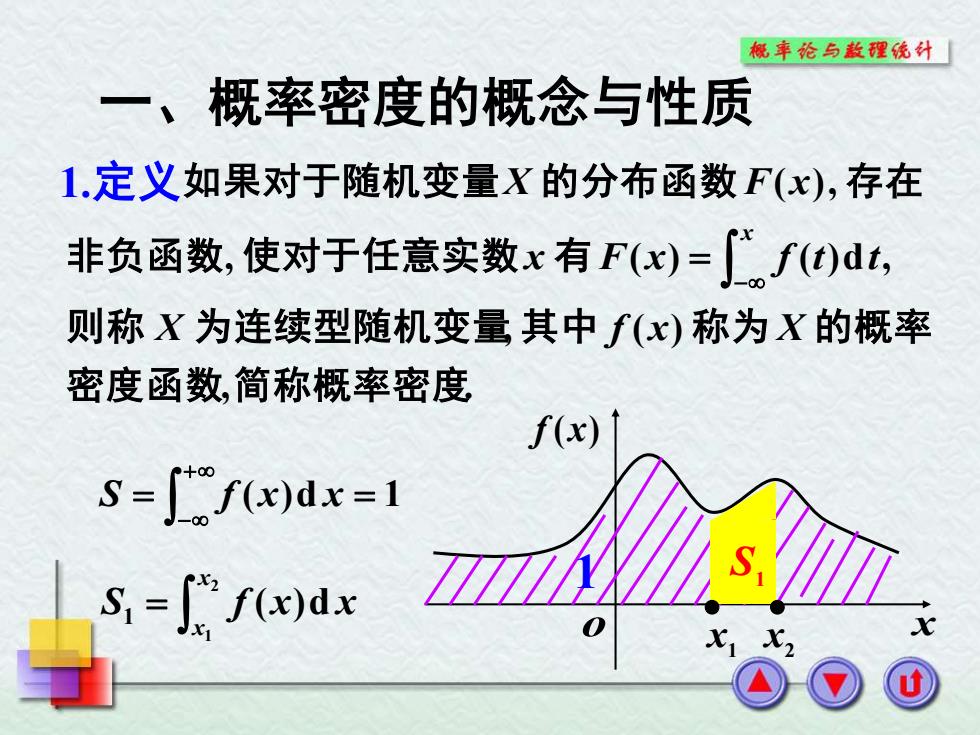
概车纶与散理统外「 一、概率密度的概念与性质 1.定义如果对于随机变量X的分布函数F(x),存在 非负函数，使对于任意实数x有F(x)=,f)dt, 则称X为连续型随机变量其中f(x)称为X的概率 密度函数，简称概率密度 f(x) S=[f(x)dx=1 S=f(x)dx X

, . , ( ) , ( ) ( )d , ( ), 密度函数 简称概率密度 则 称 为连续型随机变量 其 中 称 为 的概率 非负函数 使对于任意实数 有 如果对于随机变量 的分布函数 存 在 X f x X x F x f t t X F x x − = 一、概率密度的概念与性质 1.定义 o x f (x) 1 = ( )d = 1  + − S f x x S1 S f x x x x ( )d 2 1 1  = 1 x • 2 x •

概華论与款醒硫外 性质 (1)f(x)≥0； (2)∫mf(x)dx=1; ④

性质 (1) f (x)  0; (2) ( )d = 1;  + − f x x

概车纶与款理统外 同时得以下计算公式 P{X≤ay=Fa=“fx)dx, P{X>a}=1-P{X≤}=1-F(a) =Jfx)dx-∫fx)dx -f(x)dx+f(x)dx-f(x)dx. (4)若f(x)在点x处连续，则有F'(x)=f(x)

(4) 若 f (x) 在 点 x 处连续,则 有F(x) = f (x). P{X  a} = F(a) f (x)d x, a − = P{X  a} = 1 − P{X  a} f x x f x x a ( ) d ( ) d  −  − = − = 1− F(a) f x x f x x a ( )d ( )d    − − = + f (x)d x. a  = 同时得以下计算公式

概華论与款醒硫外 注意对于任意可能值a,连续型随机变量取a 的概率等于零即 P{X=}=0. Pa+△x 证明PX=a=fx)dx=0. 由此可得 P{a≤X≤b}=P{a<X≤b}=P{a≤X<b} =P{a<X<b}. 连续型随机变量取值落在某一 区间的概率与区间的开闭无关

注意 对于任意可能值 a ,连续型随机变量取 a 的概率等于零.即 P{X = a} = 0. 证明 P{X = a} = 0. 由此可得 f x x a x x a lim ( )d 0  +  → = 连续型随机变量取值落在某一 区间的概率与区间的开闭无关 P{a  X  b}= P{a  X  b} = P{a  X  b} = P{a  X  b}

概车纶与款理统外 注意 若X是连续型随机变量，{X=}是不 可能事件，则有P{X=}=0. 若P{X=a}=0, 连续型 则不能确定{X=是不可能事件 若X为离散型随机变量， {X=a}是不可能事件台P{X==0. 离散型

P{X = a} = 0. 若X是连续型随机变量，{ X=a }是不 可能事件，则有 若 P{X = a} = 0, {X = a}是不可能事件  P{X = a} = 0. 若 X 为离散型随机变量, 注意 连 续 型 离 散 型 则不能确定{X = a}是不可能事件

概華论与款醒硫外「 例1设随机变量X具有概率密度 kx, 0≤x<3, f(x)=2- 2 3≤x≤4， 0, 其它 ()确定常数k; (2)求X的分布函数； 求P1<X≤ 解()由∫f(x)dx=1

}. 27 (3) {1 (1) ; (2) ; 0, . , 3 4, 2 2 , 0 3, ( )   −     = P Xk Xx x kx x f x X 求 确定常数 求 的分布函数 其它 设随机变量 具有概率密度 解 (1) ( )d 1, − 由 f x x = 例 1

概率伦与散理统针」 得udx+2-ax=1解之得君 (2)由k=知X的概率密度为 6 6 0≤x<3, f(x)={2- 235x54 0, 其它

由k 知 X 的概率密度为 6 1 (2) =          −     = 0, . , 3 4, 2 2 , 0 3, 6 ( ) 其它 x x x x f x )d 1, 2 d (2 3 0 4 3 + − =   x x 得 kx x . 6 1 解之得 k =

概華论与款醒统外 由F(x)=nfx)dx得 0,x<0, dx 0sx<3 6 F(x)= 心ax+2-iux,3≤x<4 1,x≥4

          + −      =    1, 4. )d , 3 4, 2 d (2 6 d , 0 3, 6 0, 0, ( ) 3 0 3 0 x x x x x x x x x x F x x x 由  得 − = x F(x) f (x)d x

概车纶与款理统外 0, x<0, x2 0≤x<3, 即F(x)= 12' -3+2r2 ， 3≤x<4, 1, x≥4. PI<K孕=F-0=装

          − + −      = 1, 4. , 3 4, 4 3 2 , 0 3, 12 0, 0, ( ) 2 2 x x x x x x x 即 F x } 2 7 (3) P{1  X  ) (1) 2 7 = F( − F . 48 41 =