《概率论与数理统计》课程教学资源（PPT课件）第三章 多维随机变量及其分布 第五节 两个随机变量的函数的分布

概華论与款醒统外 第五节两个随机变量的函数的分布 一、问题的引入 二、离散型随机变量函数的分布 三、连续型随机变量函数的分布 四、小结

二、离散型随机变量函数的分布 三、连续型随机变量函数的分布 四、小结 一、问题的引入 第五节 两个随机变量的函数的分布

概车纶与款理统外 一、问题的引入 有一大群人，令X和Y分别表示一个人的 年龄和体重，Z表示该人的血压，并且已知Z与 X,Y的函数关系Z=g(X,Y),如何通过X,Y的 分布确定Z的分布. 为了解决类似的问题下面 我们讨论随机变量函数的分布

. , ( , ), , , , , 分布确定 的分布 的函数关系 如何通过 的 年龄和体重 表示该人的血压 并且已知 与 有一大群人 令 和 分别表示一个人的 Z X Y Z g X Y X Y Z Z X Y = 为了解决类似的问题下面 我们讨论随机变量函数的分布. 一、问题的引入

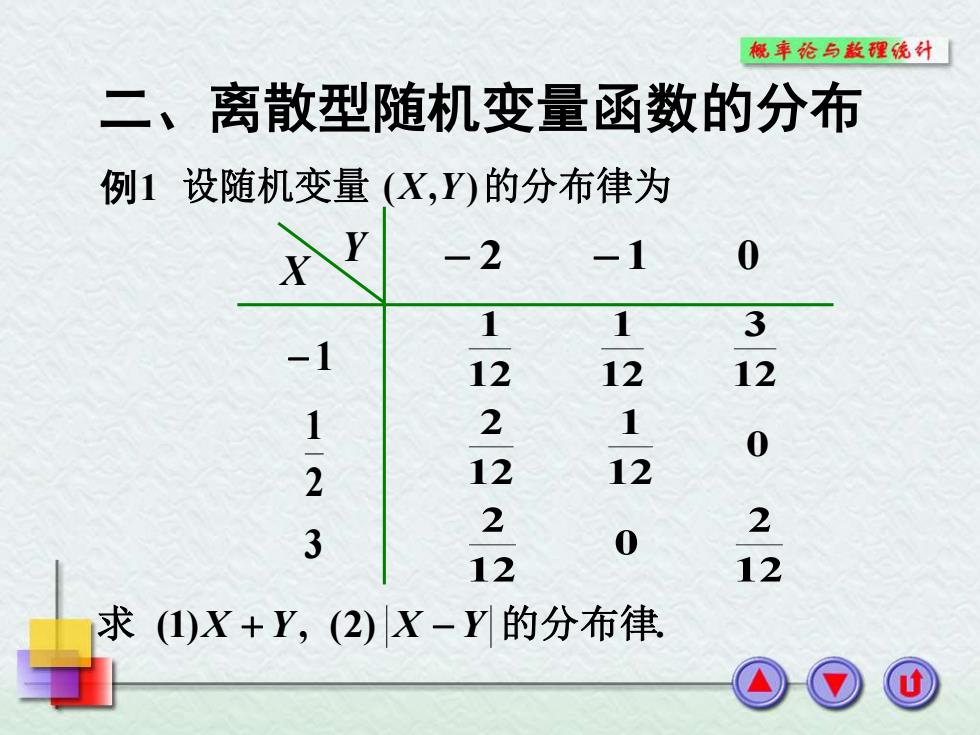
概率论与款程统针「 二、离散型随机变量函数的分布 例1设随机变量(X,Y的分布律为 -2 -1 0 1 1 3 -1 12 12 12 1 2 1 0 12 12 3 2 0 2 12 12 求（①）X+Y,(2)X-Y的分布律

二、离散型随机变量函数的分布 X Y − 2 − 1 0 − 1 2 1 3 12 3 12 1 12 1 0 12 1 12 2 12 2 0 12 2 例1 设随机变量 (X,Y)的分布律为 求 (1)X + Y, (2) X −Y 的分布律

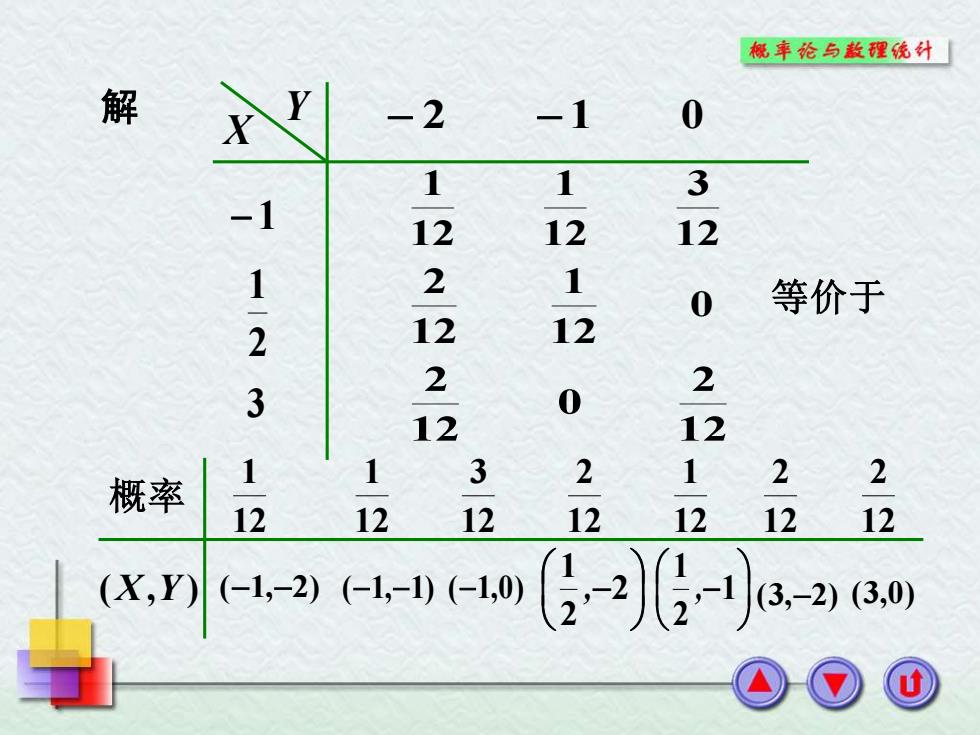
概率伦与款程统针」 解 X -2 -1 0 1 1 3 -1 12 12 12 1 2 1 0 等价于 2 12 12 2 2 3 0 12 12 1 概率 1 3 2 122 12 12 12 12 12 1212 (X,) (-1,-2)(-1,-101,0 -2g-2a0

概率 ( X , Y ) ( − 1 , − 2 ) 121 (−1,−1) 121 (−1,0) 123   −2 21 , 122   −1 21 , 121 (3,−2) 122 (3,0) 122 X Y − 2 − 1 0 − 1213 123 121 121 0 121 122 122 0 122 解 等价于

概華伦与款程统外 概率 1 2 2 1 2 12 12 1212 1212 12 (X,Y -1-2l-w(2-2G8-230, X+Y-3 -21- 13 5 3 X-Y 1 0 1 53 2 2

概率 (X,Y ) (−1,−2) 12 1 (−1,−1) 12 1 (−1,0) 12 3       ,−2 2 1 12 2       ,−1 2 1 12 1 (3,−2) 12 2 (3,0) 12 2 X +Y − 3 − 2 − 1 2 3 − 2 1 − 1 3 X −Y 1 0 1 2 5 2 3 5 3

概车纶与款理统外「 所以X+Y,X-Y的分布律分别为 X+y-3 -2-1 3 1 13 2 2 P 1 3 2 1 2 2 1 12 12 12 12 12 12 5 X-Y 0 1 3-2 5 3 2 1 4 2 1 2 2 P 12 12 12 12 12 12

X +Y P − 3 − 2 − 1 2 3 − 2 1 − 1 3 12 1 12 1 12 3 12 2 12 1 12 2 12 2 X −Y P 0 1 2 5 2 3 5 3 12 4 12 1 12 2 12 1 12 2 12 2 所以 X + Y, X −Y 的分布律分别为

概率伦与款理统外 结论 若二维离散型随机变量的联合分布律为 P{X=x,Y=yj}=P,i,j=1,2,., 则随机变量函数Z=g(X,Y)的分布律为 P(Z==P(g(X,Y)= =∑Pg, k=1,2,. Zk=g(xiyi)

结论 若二维离散型随机变量的联合分布律为 P{X = x ,Y = y } = p , i, j = 1,2,  , i j ij 则随机变量函数Z = g(X,Y)的分布律为 { } { ( , ) } k k P Z = z = P g X Y = z , 1,2, . ( ) =  =  = p k k i j z g x y ij

概车纶与散理统针「 例2设两个独立的随机变量X与Y的分布律为 X 3 Y 2 4 P 0.3 0.7 P 0.6 0.4 求随机变量Z=X+Y的分布律. 解因为X与Y相互独立，所以 P(X=xi,Y=yi}=P(X=xi)P(Y=yi}, 2 4 得 0.18 0.12 30.42 0.28

例2 设两个独立的随机变量 X 与 Y 的分布律为 X PX 1 3 0.3 0.7 Y PY 2 4 0.6 0.4 求随机变量 Z=X+Y 的分布律. { , } { } { }, i j i j P X = x Y = y = P X = x P Y = y 得 Y X 2 4 1 3 0.18 0.12 0.42 0.28 解 因为 X 与 Y 相互独立, 所以

概華论与款醒硫外 P (X,Y) Z=X+Y 24 0.18 (1,2) 3 1 0.180.12 可得 0.12 (1,4) 5 3 0.420.28 0.42 (3,2) 5 0.28 (3,4) 7 Z=X+Y 3 5 1 所以 P 0.18 0.54 0.28

可得 (X,Y ) (3,4) (3,2) (1,4) (1,2) P 0.18 0.12 0.42 0.28 Z = X +Y 3 5 5 7 所以 Z = X +Y P 3 5 7 0.18 0.54 0.28 Y X 2 4 1 3 0.18 0.12 0.42 0.28

概车纶与散理统外「 例3设相互独立的两个随机变量X,Y具有同一 分布律，且X的分布律为 X 0 1 P 0.5 0.5 试求：Z=max(X,Y)的分布律， 解因为X与Y相互独立， 所以P{X=i,Y=}=P{X=P{Y=, 0 1 于是 0 1/221/22 1 1/22 1/22

例3 设相互独立的两个随机变量X, Y 具有同一 分布律,且 X 的分布律为 X P 0 1 0.5 0.5 试求 : Z = max(X,Y )的分布律. 所以 P{X = i,Y = j} = P{X = i}P{Y = j}, 于是 X Y 0 1 1 0 2 1 2 2 1 2 2 1 2 2 1 2 解 因为X与Y相互独立