
概车纶与款理统外 第四节 区间估计 一、区间估计的基本概念 二、典型例题 三、小结
第四节 区间估计 一、区间估计的基本概念 二、典型例题 三、小结

概率伦与款程统外 一、区间估计的基本概念 1.置信区间的定义 设总体X的分布函数F(x;)含有一个未知参 数0,对于给定值a(0<a<1),若由样本X1,X2,., X,确定的两个统计量 0=(X1,X2,.,Xm)和0=0(X1,X2,.,Xm)满足 P{0(X1,X2,Xn)<0<0X1,X2,Xn)}=1-a, 则称随机区间0,0)是0的置信度为-α的置信区 间,和分别称为置信度为-α的双侧置信区间 的置信下限和置信上限1-a为置信度
一、区间估计的基本概念 1. 置信区间的定义 { ( , , , ) ( , , , )} 1 , ( , , , ) ( , , , ) , (0 1), , , , ( ; ) 1 2 1 2 1 2 1 2 1 2 = − = = n n n n n P X X X X X X X X X X X X X X X X F x 和 满 足 确定的两个统计量 数 对于给定值 若由样本 设总体 的分布函数 含有一个未知参 , 1 . , 1 ( , ) 1 的置信下限和置信上限 为置信度 间 和 分别称为置信度为 的双侧置信区间 则称随机区间 是 的置信度为 的置信区 − − −

概车纶与款理统外 关于定义的说明 被估计的参数虽然未知,但它是一个常数, 没有随机性,而区间(,0)是随机的. 因此定义中下表达式 P{0(X1,X2,.,Xn)<0<0(X1,X2,Xn)}=1-a 的本质是: 随机区间(但,0)以1-a的概率包含着参数的真值, 而不能说参数以1-a的概率落入随机区间(但,0)
关于定义的说明 , ( , ) . , , 没有随机性 而区间 是随机的 被估计的参数 虽然未知 但它是一个常数 : { ( , , , ) ( , , , )} 1 1 2 1 2 的本质是 因此定义中下表达式 P X X Xn X X Xn = − 1 ( , ). ( , ) 1 , 而不能说参数 以 的概率落入随机区间 随机区间 以 的概率包含着参数 的真值 − −

概華论与款醒硫外 另外定义中的表达式 P{0(X1,X2,Xn)<B<8(X1,X2,Xn)}=1-a 还可以描述为: 若反复抽样多次(各次得到的样本容量相等,都是) 每个样本值确定一个区间(但,0), 每个这样的区间或包含0的真值或不包含0的真值, 按伯努利大数定理,在这样多的区间中, 包含真值的约占100(1-)%,不包含的约占100a%
: { ( , , , ) ( , , , )} 1 1 2 1 2 还可以描述为 另外定义中的表达式 P X X Xn X X Xn = − 若反复抽样多次(各次得到的样本容量相等,都是n) 每个样本值确定一个区间( , ), 按伯努利大数定理, 在这样多的区间中, 包含真值的约占100(1−)%,不包含的约占100%. 每个这样的区间或包含 的真值或不包含 的真值
概车纶与款理统外 例如若=0.01,反复抽样1000次 则得到的1000个区间中不包含0真值的约为10个
例如 若 = 0.01, 反复抽样1000次, 则得到的1000个区间中不包含 真值的约为10个

概率伦与款醒统外「 2.求置信区间的一般步骤(共3步) (1)寻求一个样本X1,X2,.,Xn的函数: Z=Z(X1,X2,Xn0) 其中仅包含待估参数0,并且Z的分布已知 且不依赖于任何未知数(包括0). (2)对于给定的置信度1-,定出两个常数a,b, 使P{a<Z(X1,X2,.,Xm;0)<b}=1-a
2. 求置信区间的一般步骤(共3步) ( ). , ( , , , ; ) (1) , , , : 1 2 1 2 且不依赖于任何未知参数 包 括 其中仅包含待估参数 并 且 的分布已知 寻求一个样本 的函数 Z Z Z X X X X X X n n = { ( , , , ; ) } 1 . (2) 1 , , , 1 2 = − − P a Z X X X b a b 使 n 对于给定的置信度 定出两个常数

概率伦与散理统针」 (3)若能从a<Z(X1,X2,.,Xm;0)<b得到等价的 不等式Q<0<0,其中0=(X1,X2,.,Xm) 0=0(X1,X2,.,Xn)都是统计量,那么(但,0)就 是0的一个置信度为1-α的置信区间
1 . ( , , , ) , ( , ) , ( , , , ), (3) ( , , , ; ) 1 2 1 2 1 2 是 的一个置信度为 的置信区间 都是统计量 那 么 就 不等式 其 中 若能从 得到等价的 − = = n n n X X X X X X a Z X X X b
概车纶与款理统外「 样本容量n固定,置信水平1-a增大,置信区 间长度增大,可信程度增大,区间估计精度降低. 置信水平1-a固定,样本容量n增大,置信区 间长度减小,可信程度不变,区间估计精度提高. 单击图形播放/暂停E$C键退出 单击图形播放/暂停 ESC键退出 0.4样本容量200置信水平0.05 0.4置信水平0.95样本容量100 03置信区间88 03置信区间64 0 02 0.1 0.1 10 15 20 -0.1 -0.1 10 20 -0.2 -0.2 -0.3 -0.3 -0.4 -0.4
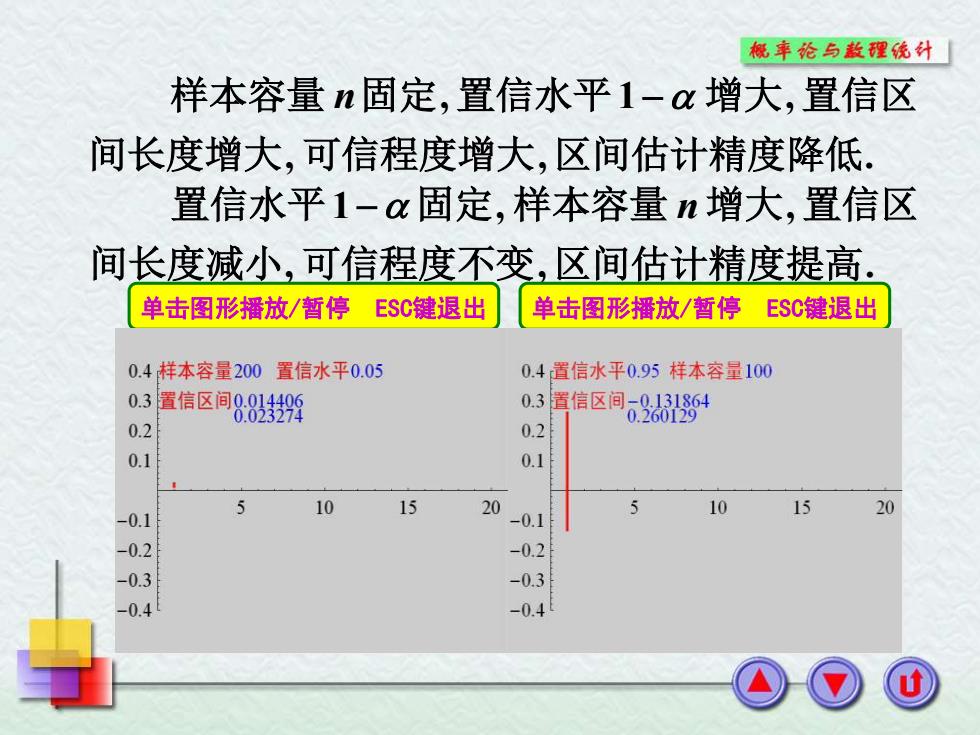
, , . , 1 , 间长度增大 可信程度增大 区间估计精度降低 样本容量 n固定 置信水平 − 增大 置信区 , , . 1 , , 间长度减小 可信程度不变 区间估计精度提高 置信水平 − 固定 样本容量 n 增大 置信区 单击图形播放/暂停 ESC键退出 单击图形播放/暂停 ESC键退出

概车纶与款理统外 二、典型例题 例1设总体X在0,1上服从均匀分布,其中0 (0>0)未知,(X1,X2,Xn)是来自总体X的样本, 给定a,求0的置信水平为1-α的置信区间. 解令Xh=max{X1,X2,.,Xn}, 由上节例4可知, n+1X。是0的无偏估计, "-1 因为X的概率密度为f(x)=了( n, 0≤x≤0, 0, 其他
二、典型例题 , 1 . ( 0) , ( , , , ) , [0, ] , 1 2 给定 求 的置信水平为 的置信区间 未知 是来自总体 的样本 设总体 在 上服从均匀分布 其中 − X X X X X n 解 max{ , , , }, 令 Xh = X1 X2 Xn 由上节例4可知, , 1 Xh 是 的无偏估计 n n + 因为 Xh的概率密度为 = − 0, . , 0 , ( ) 1 其他 x nx f x n n 例1

概華伦与款醒硫外 考察包括待估参数0的随机变量Z=X, 其概率密度为g(z)= nz"-1,0≤z≤1, 0, 其他. 对于给定的a,可定出两个常数a,b(0<a<b≤1), 满足条件P口<合<小1-a 即1-a=∫nz-dz=b"-a", 户P告<0}-1a告公为信风同
, Xh Z = = − 0, . , 0 1, ( ) 1 其他 nz z g z n 其概率密度为 对于给定的,可定出两个常数a,b(0 a b 1), 1 , = − b X P a 满足条件 h 1 d , 1 n n b a n − = nz z = b − a − 即 = 1 −, a X b X P h h , 为置信区间. a X b Xh h 考察包括待估参数 的随机变量