
第二节 边缘分布 在己知二维随机变量的联合分布的前提下,有时候我 们会感兴趣其中某个变量的分布,并希望能由己知的二 维随机变量的分布函数Fx,y)求得。 事实上,由二维随机变量(X,)的分布函数Fx,y),可以 得到它的两个分量X和Y的分布函数为 Fx(x)=P{X≤x=P{X≤x,Y≤+o=F(x,+o) F,(y)=P{Y≤y=P{X≤+oo,Y≤yF(+o,y) 分布函数Fx(x)和Fy)分别称为二维随机变量(X,Y)关于 X和Y的边缘分布。 2024年8月27日星期二 目录 上页 下页 返回
2024年8月27日星期二 1 目录 上页 下页 返回 第二节 边缘分布 事实上,由二维随机变量(X, Y)的分布函数F(x,y),可以 得到它的两个分量X和Y的分布函数为 F x X ( ) = P X x= + P X x Y , = + F x( , ) F y Y ( ) = P Y y= + P X Y y , = + F y ( , ) 分布函数FX (x)和FY (y)分别称为二维随机变量(X, Y)关于 X和Y的边缘分布。 在已知二维随机变量的联合分布的前提下,有时候我 们会感兴趣其中某个变量的分布,并希望能由已知的二 维随机变量的分布函数F(x,y)求得

二维离散型随机变量的边缘分布律 X y2 于是 P12 Pu X2.Xi X2 p21 P22 P2j P2 PP. Pa Pi2 . P P Y y y2 .y P2 p Pp1p2.p, p.=P{X=x}=∑Pi=l2,. 二维离散型随机变量的边 缘分布是一维离散型分布 P,=P{=y}=∑Pj=12. 2024年8月27日星期二 2 目录 上页 下页 返回
2024年8月27日星期二 2 目录 上页 下页 返回 二维离散型随机变量的边缘分布律 1 2 1. 2. . . . . . i i X x x x P p p p 1 2 .1 .2 . . . . . j j Y y y y P p p p 1 2 1 11 12 1 2 21 22 2 1 2 . . . . . . . . . . . . . . . . . . . . j j j i i i ij y y y x p p p x p p p x p p p X Y P p1. 2. p i. p . . P .1 p .2 p . j . p . 二维离散型随机变量的边 缘分布是一维离散型分布 1 , 1,2, i i ij j p P X x p i + = = = = = 1 , 1,2, j j ij i p P Y y p j + = = = = = 于是
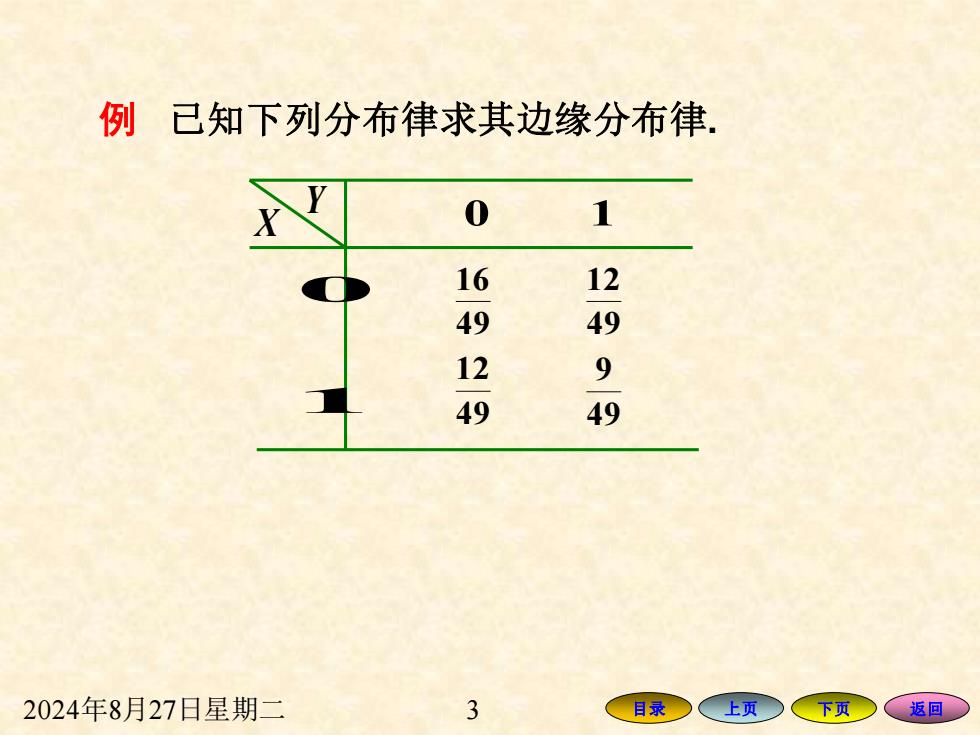
例已知下列分布律求其边缘分布律 0 1 16 12 49 49 9 49 49 2024年8月27日星期二 3 目录 上页 下页今 返回
2024年8月27日星期二 3 目录 上页 下页 返回 例 已知下列分布律求其边缘分布律. X Y 0 1 49 16 49 12 49 12 49 9 1 0
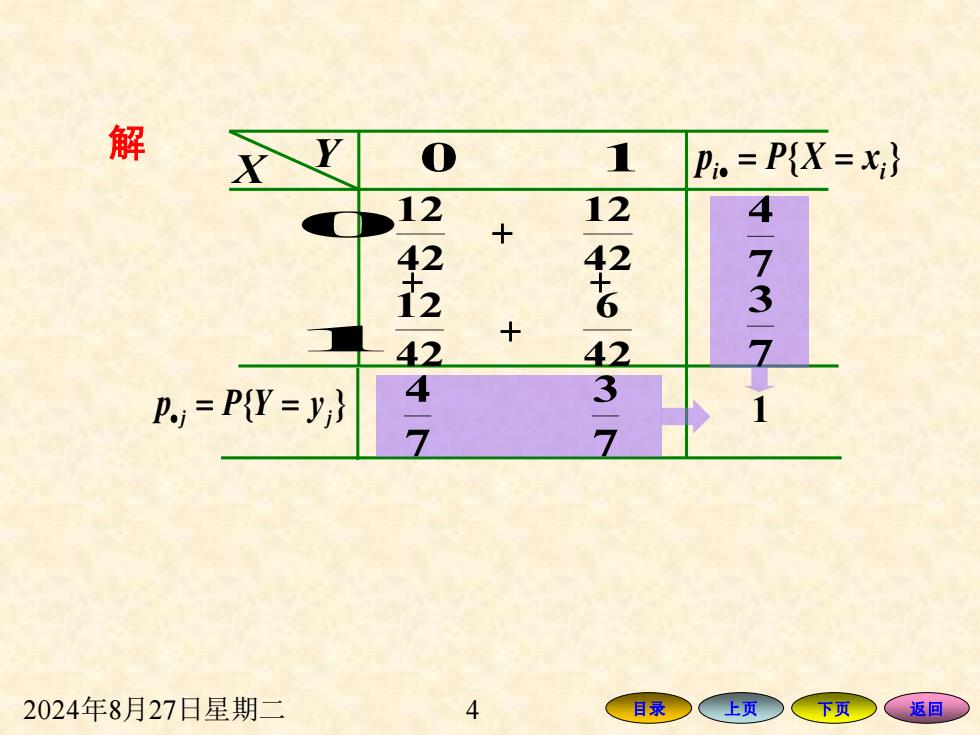
解 0 1 Pi=P(X=x;} 12 12 4 老 73 42 P.)=P(Y=y) 47 13-7 1 2024年8月27日星期二 4 目录 、上页> 下页 返回
2024年8月27日星期二 4 目录 上页 下页 返回 X Y 0 1 42 12 42 12 42 12 42 6 1 0 { } i i p = P X = x • { } j j p = P Y = y • 解 + + + + 7 4 7 3 1 7 4 7 3

例:己已知(X,)的分布律如下,求(X,)关于X和Y的边 缘分布律。 解:(X,关于X的边缘分布律为 0 1 2 01 2 1 0 5 91 33 22 22 P 33 22 22 1 103 2-1 0 (X,)关于Y的边缘分布律为 0 12 2 11 0 0 14 161 P 33 33 11 2024年8月27日星期二 5 目录 上页 下页 返回
2024年8月27日星期二 5 目录 上页 下页 返回 X Y 0 1 2 5 5 1 0 33 22 22 10 2 1 0 33 11 1 2 0 0 11 例:已知(X, Y)的分布律如下,求(X, Y)关于X和Y的边 缘分布律。 0 1 2 18 9 1 33 22 22 X P 0 1 2 14 16 1 33 33 11 Y P 解:(X, Y)关于X的边缘分布律为 (X, Y)关于Y的边缘分布律为
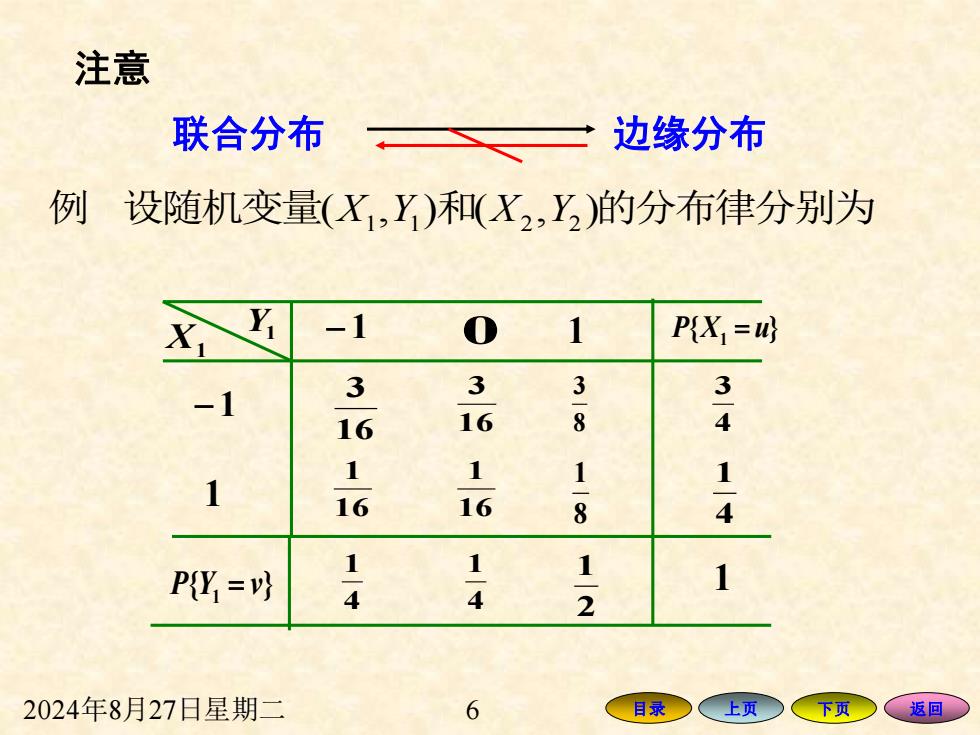
注意 联合分布 边缘分布 例设随机变量(X,Y)和(X,Y)的分布律分别为 -1 0 1 P(X=u) -1 3 3 3-8 16 16 4 1 1 1 1 16 16 8 4 Pg=以 1-4 1-4 2 1 2024年8月27日星期二 6 目录○ 上页 下页 返回○
2024年8月27日星期二 6 目录 上页 下页 返回 注意 联合分布 边缘分布 例 设随机变量(X1 ,Y1 )和(X2 ,Y2 )的分布律分别为 − 1 X1 Y1 0 16 3 16 1 { } P X1 = u { } 1 P Y = v 4 3 4 1 1 4 1 2 1 − 1 16 3 8 3 16 1 8 1 4 1 1 1
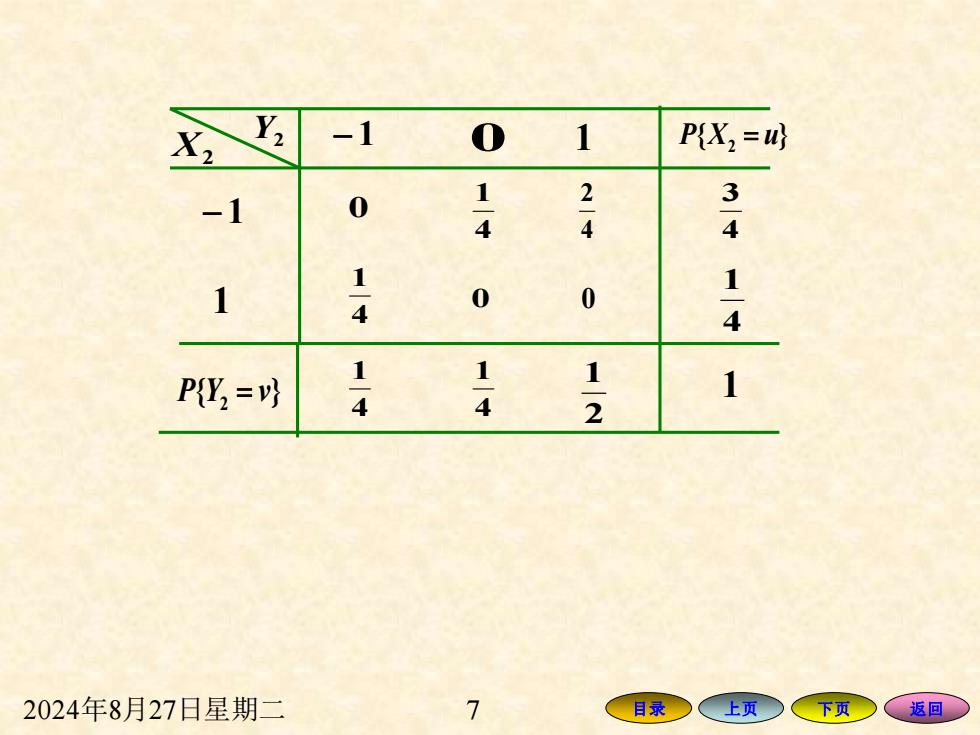
Y -1 0 1 P{X2= -1 0 2 3 4 4 4 1 1 1-4 0 0 4 P,=以 14 4 1-2 1 2024年8月27日星期二 7 目录 (上页下页 返回
2024年8月27日星期二 7 目录 上页 下页 返回 − 1 X2 Y2 0 0 4 1 { } P X2 = u { } 2 P Y = v 4 3 4 1 1 4 1 2 1 − 1 4 1 4 2 0 0 4 1 1 1

二维连续型随机变量的边缘概率密度 一方面,我们有:Fx(x)=P{X<x}=f(x) 另一方面,我们有: F:(x)=P{X<x.Y<+f(x.)dy ds 所以,fx(x)=f(x,y)同理,f(y)=「f(xy) 分别称f(x)和y)为二维随机变量(X,)关于X和Y的边缘 概率密度。 2024年8月27日星期二 8 目录 上页 下页 返回
2024年8月27日星期二 8 目录 上页 下页 返回 一方面,我们有: F x P X x X ( ) = X ( ) x f x dx − = 另一方面,我们有: F x P X x Y X ( ) = + , ( , ) x f x y dy dx + − − = 所以, f x f x y dy X ( ) ( , ) + − = 同理, f y f x y dx Y ( ) ( , ) + − = 二维连续型随机变量的边缘概率密度 分别称fX (x)和fY (y)为二维随机变量(X, Y)关于X和Y的边缘 概率密度

例:设二维随机变量(X,)在区域D={(x,y)0<x<2,0<~1} 上服从均匀分布。求(X,)关于X和Y的边缘概率密度。 解:由题意可知:(X,)的概率密度为 以行P 其它 当x≤0或x心2时, 由于f(x,)=0.故 fx(x)=∫f(,y)=」0=0 当0<x<2时, (=xy)== 2024年8月27日星期二 目录 上页 下页 返回
2024年8月27日星期二 9 目录 上页 下页 返回 例:设二维随机变量(X, Y)在区域D={(x,y)|0<x<2,0<y<1} 上服从均匀分布。求(X, Y)关于X和Y的边缘概率密度。 解:由题意可知: (X, Y)的概率密度为 1 , ( , ) , ( , ) 2 0, x y D f x y = 其它. 当x≤0或x≥2时, 由于f (x, y) = 0.故 f x f x y dy dy X ( ) ( , 0 0 ) + + − − = = = 当0<x<2时, f x f x y dy X ( ) ( , ) + − = 1 0 1 1 d 2 2 = = y

因此 fx()= 0, 其它 同理可得 0)=人0y<1 -0, 其它. 2024年8月27日星期二 10 目录○ 上页 下页 返回
2024年8月27日星期二 10 目录 上页 下页 返回 因此 1 , 0 2, ( ) 2 0, X x f x = 其它. 同理可得 1, 0 1, ( ) 0, Y y f y = 其它