
第四章 随机变量的数字特征 一、离散型随机变量的数学期望 定义:设X是离散型随机变量,其分布律为 P{X=x}=p,i=1,2, 若级数∑xP,绝对收敛,则称级数∑xP,为X的数学期望, i记为EC).即E(X)=∑xP i=1 2024年8月27日星期二 2 目录○ 、上页 下页 返回
2024年8月27日星期二 2 目录 上页 下页 返回 一、离散型随机变量的数学期望 定义:设X是离散型随机变量,其分布律为 = = = , 1,2,. P X x p i i i 若级数 绝对收敛, 1 i i i x p = 则称级数 为X的数学期望, 1 i i i x p = 记为E(X). 即 1 ( ) i i i E X x p = = 第四章 随机变量的数字特征

一维离散型随机变量函数的数学期望 定理:设X是离散型随机变量,其分布律为 P{X=x}=p,i=1,2,. 对任一实值函数g(),若级数∑8(x)p,绝对收敛, 则有 ELg(X】=∑gx)P 2024年8月27日星期二 3 目录 上页 下页今 、返回
2024年8月27日星期二 3 目录 上页 下页 返回 一维离散型随机变量函数的数学期望 定理:设X是离散型随机变量,其分布律为 = = = , 1,2,. P X x p i i i 若级数 绝对收敛, 1 ( )i i i g x p = 则有 1 [ ( )] ( )i i i E g X g x p = = 对任一实值函数g(·)

二维离散型随机变量函数的数学期望 定理:设X,)是二维离散型随机变量,其分布律为 P(X=x,Y=y)=P,ij=1,2,. 若级数∑∑gx,y,)P,绝对收敛,则有 Eg(X,】=∑∑3,y,P, i=1i=1 2024年8月27日星期二 4 目录○ 、上页 下页 返回
2024年8月27日星期二 4 目录 上页 下页 返回 定理:设(X,Y)是二维离散型随机变量,其分布律为 ( , ) , , 1,2, P X x Y y p i j = = = = i j ij 若级数 绝对收敛, 1 1 ( , ) i j ij i j g x y p = = 则有 1 1 [ ( , )] ( , ) i j ij i j E g X Y g x y p = = = 二维离散型随机变量函数的数学期望

二、连续型随机变量的数学期望 定义:设X是连续型随机变量,其概率密度为f(x), 若积分」f(x)d绝对收敛,则称级数∫f(x)dx为X的 数学期望,记为E).即 E(X=∫fx)d 2024年8月27日星期二 5 目录○ 、上页下页 返回
2024年8月27日星期二 5 目录 上页 下页 返回 二、连续型随机变量的数学期望 定义:设X是连续型随机变量,其概率密度为f (x). 若积分 xf x x ( )d 绝对收敛, + − 则称级数 xf x x ( )d 为X的 + − 数学期望,记为E(X). 即 E X xf x x ( ) ( )d + − =

一维连续型随机变量函数的数学期望 定理:设X是连续型随机变量,其概率密度为f(x) 若积分」g(x)f(x)dr绝对收敛,则有 E[g(X)]=g(x)f(x)dx 2024年8月27日星期二 6 目录上页下页 返回
2024年8月27日星期二 6 目录 上页 下页 返回 一维连续型随机变量函数的数学期望 定理:设X是连续型随机变量,其概率密度为f (x). 则有 E g X g x f x x ( ) ( ) ( )d + − = 若积分 g x f x x ( ) ( )d 绝对收敛, + −

二维连续型随机变量函数的数学期望 定理:设连续型随机变量(X,)的概率密度为f(x,y) 若积分∫gx,f(x,dd绝对收敛,则有 E[g(X,Y】=∫r"gx,)fx,y)dd 2024年8月27日星期二 7 目录○ 上页>(下页○ 返回
2024年8月27日星期二 7 目录 上页 下页 返回 定理:设连续型随机变量(X,Y) 的概率密度为f (x,y). 二维连续型随机变量函数的数学期望 若积分 g x y f x y x y ( , ) ( , )d d 绝对收敛, + + − − 则有 E g X Y g x y f x y x y ( , ) ( , ) ( , )d d + + − − =

三、数学期望的性质 1.E(C)=C,C为常数, 2.E(C)=CE(),C为常数: 3.设X和Y是两个随机变量,则有E(X+)=E()+E(Y) 4.设X和Y是两个相互独立的随机变量,则有 EXYEXE(Y) 2024年8月27日星期二 8 目录 上页 下页 返回
2024年8月27日星期二 8 目录 上页 下页 返回 三、数学期望的性质 1. E(C)=C, C为常数; 2. E(CX)=CE(X), C为常数; 3. 设X和Y是两个随机变量,则有E(X+Y)=E(X)+E(Y). 4. 设X和Y是两个相互独立的随机变量,则有 E(XY)=E(X)E(Y)

四、方差的定义及计算公式 定义:设X是一个随机变量,若E[x-E(X}存在 则称E[x-(X}为X的方差。记为DC)或ar 即 D(X)=Var(X)=E[X-E(X) 称√D(X为X的均方差或标准差。记为σ() D(X)= x-E(X)PPX=x},离散型情形 k 广[x-E(X)]'f(x)dk,连续型情形 推论 D(X)=E(X-E(X) 2024年8月27日星期二 目录 上页 下页 返回
2024年8月27日星期二 9 目录 上页 下页 返回 四、方差的定义及计算公式 定义:设X是一个随机变量,若 2 E X E X − ( ) 存在, 则称 为X的方差。 2 E X E X − ( ) 记为 D (X) 或 Var (X). 2 D X Var X E X E X ( ) ( ) ( ) = = − 即 称 D X( ) 为X的均方差或标准差。记为 σ (X). − − = = − = 连续型情形 离散型情形 [ ( )] ( ) , [ ( )] { } , ( ) 2 1 2 x E X f x dx x E X P X x D X k k k 推论 D(X)=E(X2 )―[E(X)]2
五、常见分布及其期望和方差列表 分布名称 数学期望E 方差DX) 0-1分布 p pq 二项分布 np npq 泊松分布 均匀分布 2 12 1 1 指数分布 元 元2 正态分布 2024年8月27日星期二 10 目录○ 上页 下页 返回
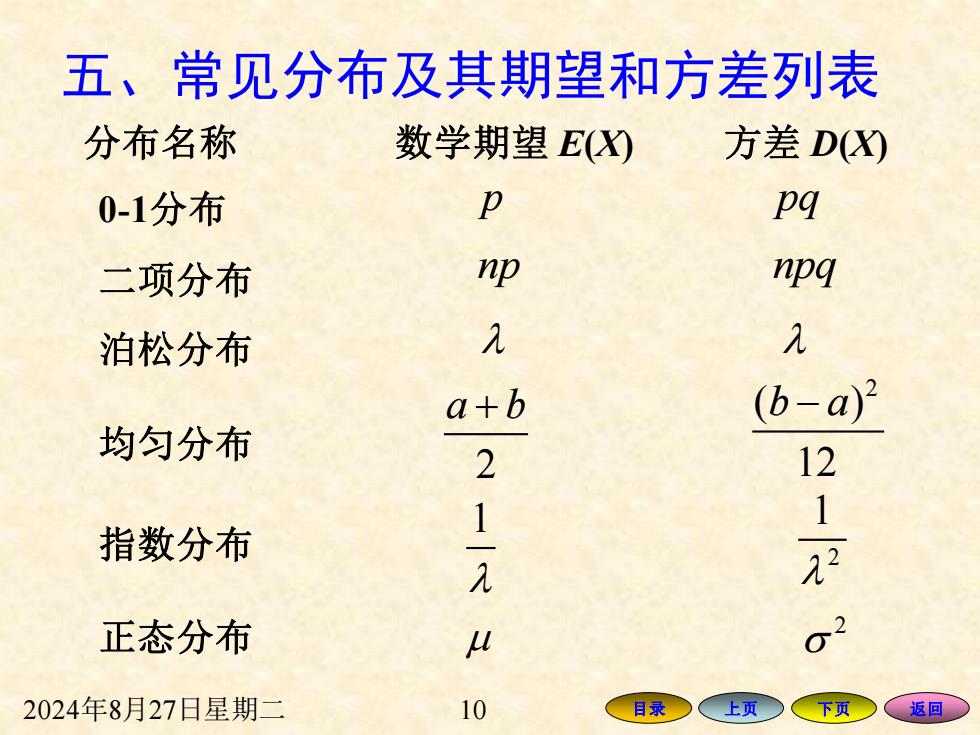
2024年8月27日星期二 10 目录 上页 下页 返回 五、常见分布及其期望和方差列表 分布名称 数学期望 E(X) 方差 D(X) 0-1分布 二项分布 泊松分布 均匀分布 正态分布 指数分布 p pq np npq 2 a b + 2 ( ) 12 b a − 1 2 2 1

六、方差的性质 1.D(C)=0,C为常数; 2.D(CX)=C2DX),DX+C)=D),C为常数; 3.设X和Y是两个随机变量,则有 D(X+Y)=D(X)+D(Y)+2E{[X-E(X)][Y-E(Y]} 特别地,当X和Y是相互独立时,有 D(X+Y)=D(X)+D(Y) 推广到n个相互独立的随机变量时,有 D(X1+X2+.+Xn)=D(X)+D(X2)+.+D(Xn) 2024年8月27日星期二 11 目录今上页> 下页 返回
2024年8月27日星期二 11 目录 上页 下页 返回 六、方差的性质 1. D(C)=0, C为常数; 2. D(CX)=C2D(X), D(X+C)=D(X), C为常数; 3. 设X和Y是两个随机变量,则有 D(X+Y)=D(X)+D(Y)+2E{[X-E(X)][Y-E(Y)]}. 特别地,当X和Y是相互独立时,有 D(X+Y)=D(X)+D(Y) 推广到n个相互独立的随机变量时,有 1 2 1 2 ( ) ( ) ( ) ( ) D X X X D X D X D X + + + = + + + n n