
概率伦与款理统外 第二节边缘分布 一、边缘分布函数 二、离散型随机变量的边缘分布律 三、连续型随机变量的边缘分布 四、小结
二、离散型随机变量的边缘分布律 三、连续型随机变量的边缘分布 一、边缘分布函数 四、小结 第二节 边缘分布
概车纶与款理统外 一、边缘分布函数 问题:已知(X,Y)的分布,如何确定X,Y的分布? F(x,y)=P{X≤x,Y≤y},F(x)=P{X≤x, P{X≤x}=P{X≤x,Y<o}=F(x,oo)=Fx(x) 0 (X,Y)关于X的边缘分布函数
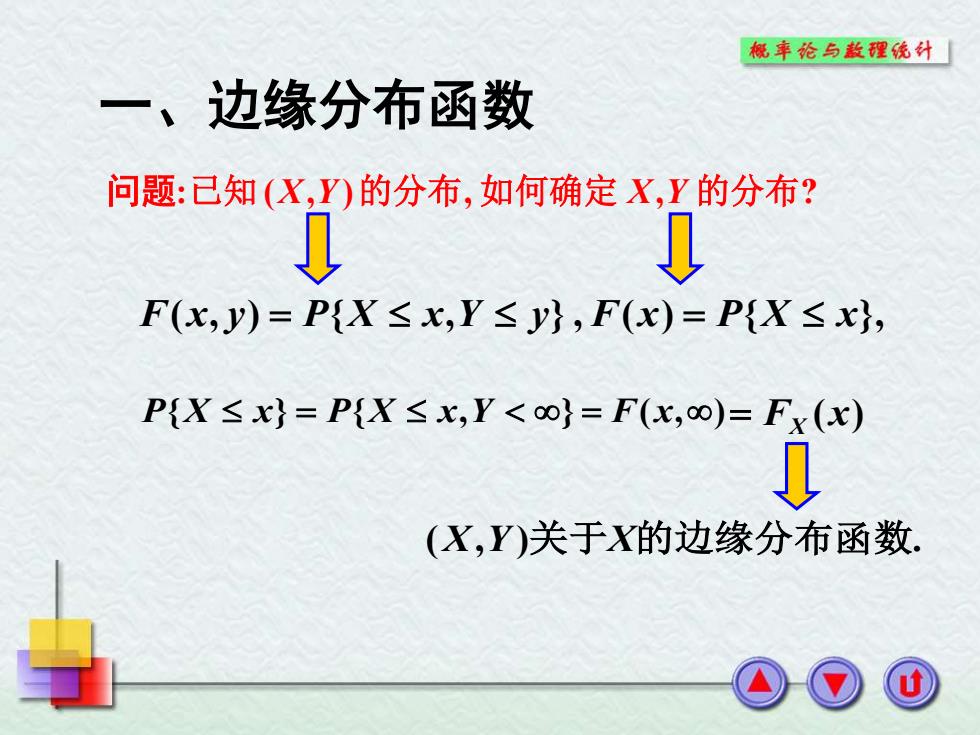
一、边缘分布函数 F(x, y) = P{X x,Y y}, F(x) = P{X x}, P{X x} = P{X x,Y } = F(x,) F (x) = X (X,Y )关于X的边缘分布函数. 问 题:已知 (X,Y )的分布, 如何确定 X,Y 的分布?

概華论与款醒硫外 定义设F(x,y)为随机变量(X,Y)的分布函数, 则F(x,y)=P{X≤x,Y≤y}. 令y→o,称P{X≤x}=P{X≤x,Y<∞}=F(x,o) 为随机变量(X,Y)关于X的边缘分布函数, 记为Fx(x)=F(x,o): 同理令x→0, Fy(y)=F(o,y)=P{X<o,Y≤y}=P{Y≤y} 为随机变量(X,Y)关于Y的边缘分布函数
F ( y) F( , y) P{X ,Y y} P{Y y} Y = = = 为随机变量 ( X,Y )关于Y 的边缘分布函数. ( , ) . , { } { , } ( , ) ( , ) { , }. ( , ) ( , ) , 为随机变量 关 于 的边缘分布函数 令 称 则 设 为随机变量 的分布函数 X Y X y P X x P X x Y F x F x y P X x Y y F x y X Y → = = = F (x) = F(x,). 记为 X 定义 同理令 x →

概车纶与款理统外「 二、离散型随机变量的边缘分布律 定义 设二维离散型随机变量X,Y)的联合分布 律为 P{X=x,Y=yj}=p,i,j=1,2,. 记 p.=∑P=PX=x},i=1,2, p=∑pg=PY=yj=1,2, 分别称p.(i=1,2,)和p(j=1,2,.)为(X,Y) 关于X和关于Y的边缘分布律
. ( 1,2, ) ( 1,2, ) ( , ) { }, 1,2, , { }, 1,2, , { , } , , 1,2, . ( , ) 1 1 关 于 和关于 的边缘分布律 分别称 和 为 记 律 为 设二维离散型随机变量 的联合分布 X Y p i p j X Y p p P Y y j p p P X x i P X x Y y p i j X Y i j j i j ij i j i ij i j ij = = = = = = = = = = = = = = • • = • = • 定义 二、离散型随机变量的边缘分布律
概率纶与款醒统外「 X X1 X2 Xi yi 11 P21 y2 P12 P22 二 PX=x=∑Pi=12,. i- PY=y}=∑Pgj=1,2
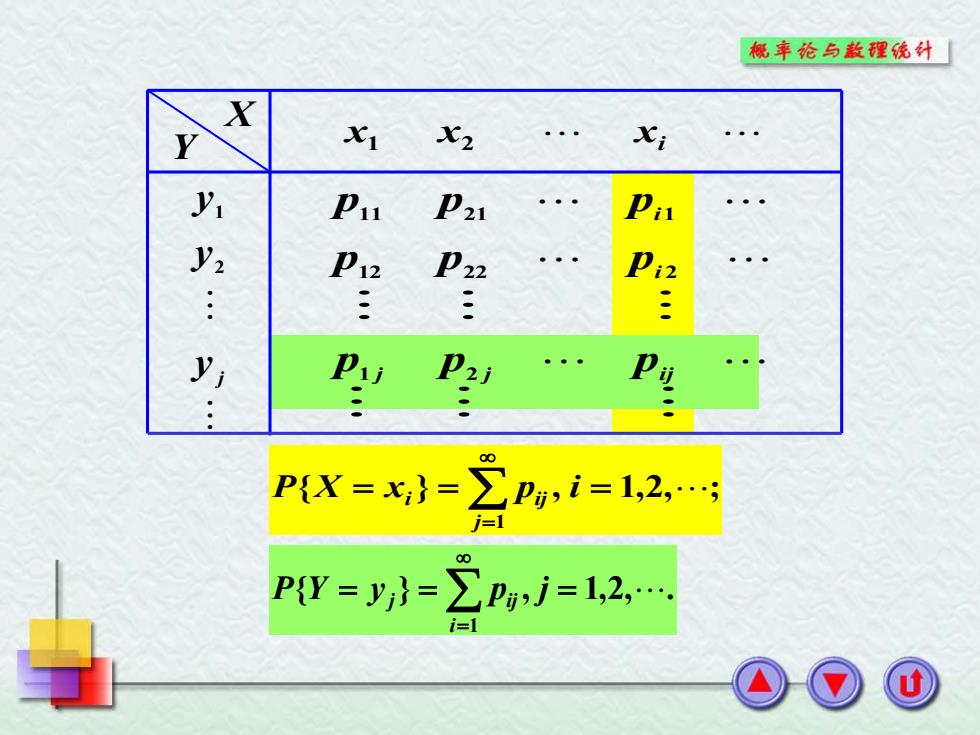
{ } , 1,2, ; 1 = = = = P X x p i j i ij { } , 1,2, . 1 = = = = P Y y p j i j ij X Y x1 x2 xi j y y y 2 1 p11 p21 pi1 p12 p22 pi 2 p1 j p2 j pij

概率伦与散理统针」 因此得离散型随机变量关于X和Y的边缘分布函 数分别为 F,()=Fx,o)=∑2pg, x≤xj=l E,U)=Fo,)=∑Pg
( ) ( , ) , 1 = = = x x j X ij i F x F x p ( ) ( , ) . 1 = = = y y i Y ij j F y F y p 因此得离散型随机变量关于X 和Y 的边缘分布函 数分别为
概華伦与款程统外 例1已知下列分布律求其边缘分布律 0 1 16 12 49 49 12 9 49 49
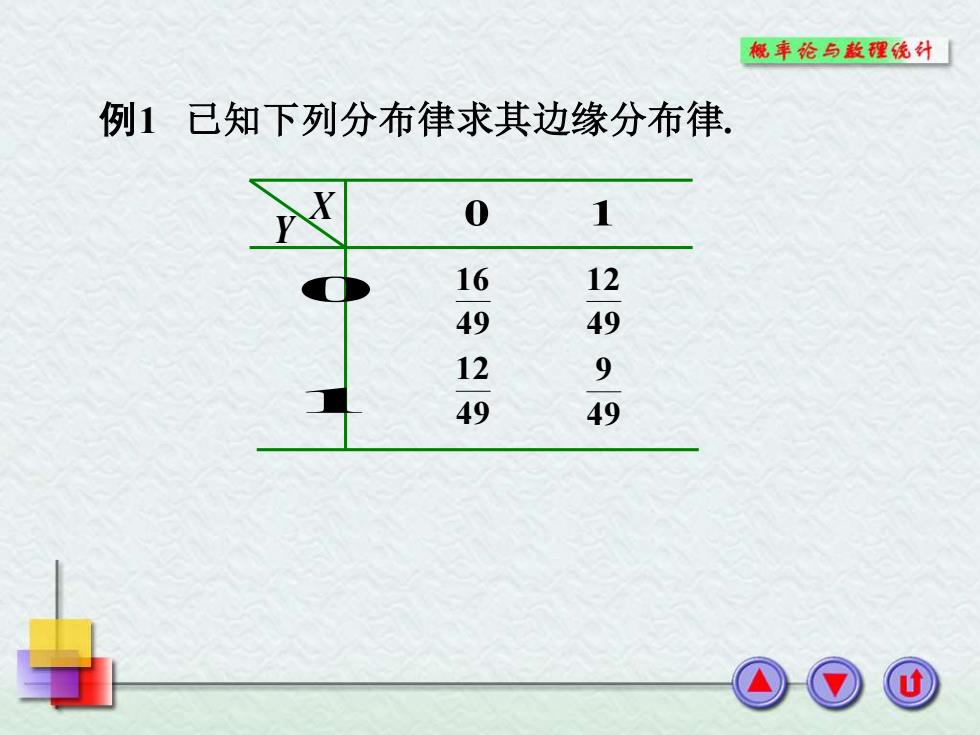
例1 已知下列分布律求其边缘分布律. X Y 0 1 49 16 49 12 49 12 49 9 1 0
棍丰伦与散程统针」 解 0 1 P.=P(Y=y} 2 12 4 + 老 73 42 + Pi.P(X=x} 4-7 13-7 注意 联合分布 二边缘分布
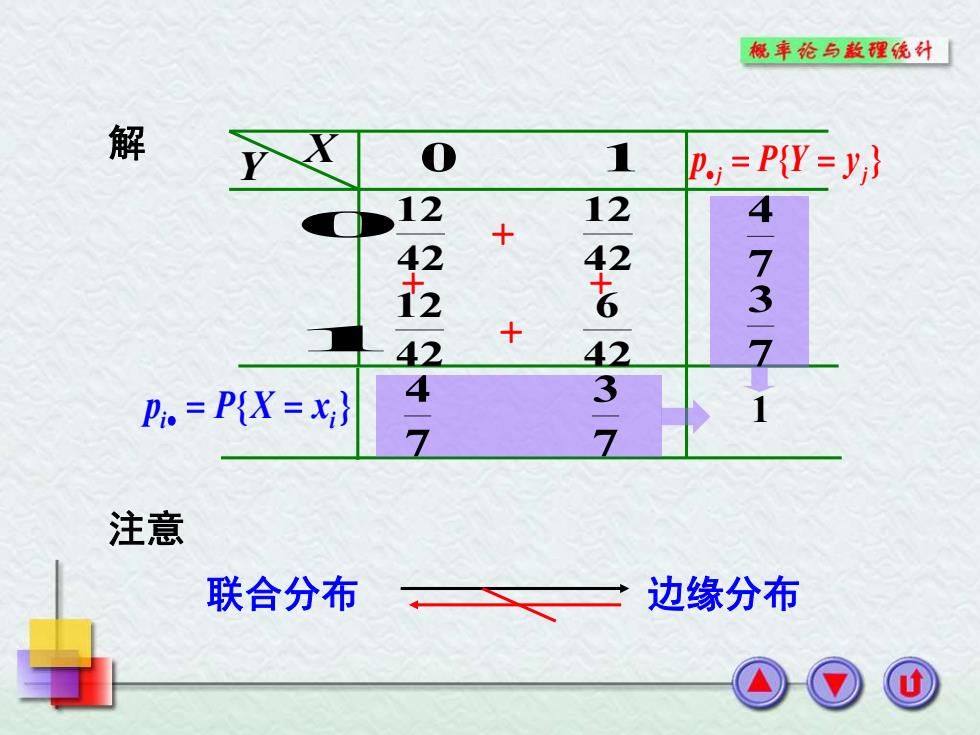
X Y 0 1 42 12 42 12 42 12 42 6 1 0 { } i i p = P X = x • { } j j p = P Y = y • 注意 联合分布 边缘分布 解 + + + + 7 4 7 3 1 7 4 7 3

概率纶与款理统外 例2一整数N等可能地在1,2,3,.,10十个值中取 一个值.设D=D(N)是能整除N的正整数的个数, F=F(N)是能整除N的素数的个数.试写出D和F 的联合分布律,并求边缘分布律. 解 样本点 12345678910 D 1223242434 F 0111121112 由此得D和F的联合分布律与边缘分布律:
解 1 2 3 4 5 6 7 8 9 10 1 2 2 3 2 4 2 4 3 4 0 1 1 1 1 2 1 1 1 2 例2 , . ( ) . . ( ) , 1,2,3, ,10 的联合分布律 并求边缘分布律 是能整除 的素数的个数 试写出 和 一个值 设 是能整除 的正整数的个数 一整数 等可能地在 十个值中取 F F N N D F D D N N N = = 由此得 D 和F 的联合分布律与边缘分布律 : 样本点 D F

棍丰伦与散理统针」 D 123 4 P{F=} 0 1/10 0 0 0 1/10 1 0 4/102/101/10 7/10 2 0 0 02/10 2/10 P(D=i 1/104/10 2/10 3/10 1 或将边缘分布律表示为 D1234 F012 P:/104/102/103/10 y10710210
D k p 1 2 3 4 1 10 4 10 2 10 3 10 F k p 0 1 2 1 10 7 10 2 10 1 2 3 4 1 10 0 0 0 0 4 10 2 10 1 10 0 0 0 2 10 D F P{F = j} 1 10 7 10 2 10 P{D = i} 1 10 4 10 2 10 3 10 1 或将边缘分布律表示为 0 1 2