《概率论与数理统计》课程教学资源（PPT课件）第一章 概率论的基本概念 第六节 独立性

概奉伦论与散理统计 第六节 独立性 一、事件的相互独立性 二、几个重要定理 三、例题讲解 四、小结

一、事件的相互独立性 二、几个重要定理 三、例题讲解 四、小结 第六节 独立性

概率论与款理统外 一、事件的相互独立性 1.引例 盒中有5个球(3绿2红)，每次取出一个，有放回 地取两次.记 A=第一次抽取，取到绿球， B=第二次抽取，取到绿球， 则有 P(BA)=P(B), 它表示A的发生并不影响B发生的可能性大小. P(BA)=P(B)P(AB)=P(A)P(B)

一 、事件的相互独立性 , , , , . 5 (3 2 ), , 第二次抽取 取到绿球 第一次抽取 取到绿球 地取两次 记 盒中有 个球 绿 红 每次取出一个 有放回   B A 则有 P(B A)  P(B), 它表示 A的发生并不影响 B 发生的可能性大小. P(B A)  P(B)  P(AB)  P(A)P(B) 1.引例

概奉论与散理统计「 2.定义 设A,B是两事件，如果满足等式 P(AB)=P(A)P(B) 则称事件A,B相互独立，简称A,B独立. 说明 事件A与事件B相互独立，是指事件A的 发生与事件B发生的概率无关

, , , . ( ) ( ) ( ) , , 则称事件 相互独立 简称 独立 设 是两事件 如果满足等式 A B A B P AB P A P B A B  事件 A 与 事件 B 相互独立,是指事件 A 的 发生与事件 B 发生的概率无关. 说明 2.定义

概率伦与敖理统外 请同学们思考 两事件相互独立与两事件互斥的关系. 两事件相互独立P(AB)=P(A)P(B): 二者之间没 两事件互斥 AB=☑ 有必然联系 例如 B 若P=P(B剧 AB 则P(AB)=P(A)P(B). 由此可见两事件相互独立，但两事件不互斥

两事件相互独立 P(AB)  P(A)P(B) 两事件互斥 AB   A B , 2 1 , ( ) 2 1 若 P(A)  P B  AB 则 P(AB)  P(A)P(B). 例如 由此可见两事件相互独立，但两事件不互斥. 两事件相互独立与两事件互斥的关系. 请同学们思考 二者之间没 有必然联系

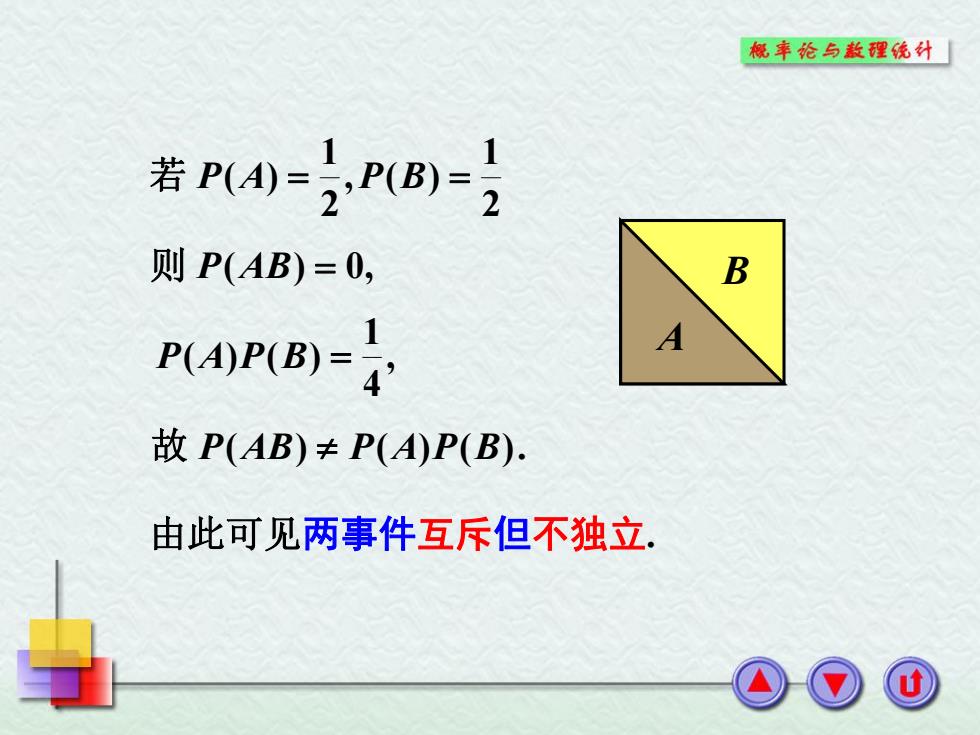
概奉论与散理统计「 若P0P®-} 则P(AB)=0, B PAPB, 故P(AB)≠P(A)P(B): 由此可见两事件互斥但不独立

A B 2 1 , ( ) 2 1 若 P(A)  P B  故 P(AB)  P(A)P(B). 由此可见两事件互斥但不独立. 则 P(AB)  0, , 4 1 P(A)P(B) 

概率伦与敖理统外 3.三事件两两相互独立的概念 定义设A,B,C是三个事件，如果满足等式 P(AB)=P(A)P(B), P(BC)=P(B)P(C), P(AC)=P(A)P(C), 则称事件A,B,C两两相互独立

3.三事件两两相互独立的概念 , , . ( ) ( ) ( ), ( ) ( ) ( ), ( ) ( ) ( ), , , , 则称事件 两两相互独立 定义 设 是三个事件 如果满足等式 A B C P AC P A P C P BC P B P C P AB P A P B A B C        

概奉论与散理统计「 4.三事件相互独立的概念 定义设A,B,C是三个事件，如果满足等式 P(AB)=P(A)P(B), P(BC)=P(B)P(C), P(AC)=P(A)P(C), P(ABC)=P(A)P(B)P(C), 则称事件A,B,C相互独立· 注意 三个事件相互独立 2三个事件两两相互独立

注意 三个事件相互独立 三个事件两两相互独立 4.三事件相互独立的概念 , , . ( ) ( ) ( ) ( ), ( ) ( ) ( ), ( ) ( ) ( ), ( ) ( ) ( ), , , , 则称事件 相互独立 定义 设 是三个事件 如果满足等式 A B C P ABC P A P B P C P AC P A P C P BC P B P C P AB P A P B A B C        

概率伦与数理统外 推广设A1,A2,An是n个事件，如果对于任意 k(1<k≤n),任意1≤i1<i2<.<ik≤n,具有等式 P(AA2.A)=P(A)P(A,).P(A), 则称A1,A,An为相互独立的事件 n个事件相互独立 n个事件两两相互独立

( ) ( ) ( ) ( ), 1 2 k 1 2 k P Ai Ai Ai  P Ai P Ai P Ai , , , . 则称 A1 A2  A n 为相互独立的事件 n 个事件相互独立 n个事件两两相互独立 任意 具有等式 设 是 个事件 如果对于任意 (1 ), 1 , , , , , 1 2 1 2 k k n i i i n A A A n k n        推广 

概奉论与散理统计 二、几个重要定理 定理一设A,B是两事件，且P(A)>0.若A,B相 互独立，则P(BA)=P(B).反之亦然， 证明 P(BA)= P(AB) P(A) P(A)P(B)=P(B) P(A) →P(BA)=P(B):

证明 ( ) ( ) ( ) P A P AB P B A  ( ) ( ) ( ) ( ) P B P A P A P B    P(B A)  P(B). , ( ) ( ). . , , ( ) 0. , 互独立 则 反之亦然 设 是两事件 且 若 相 P B A P B A B P A A B   二、几个重要定理 定理一

概率论与数理统外 定理二若A,B相互独立，则下列各对事件， A与B,A与B,A与B也相互独立. 证明 先证A与B独立. 因为A=ABUAB且(AB)(AB)=, 所以P(A)=P(AB)+P(AB), 即PAB)=P(A)-PAB)

证明 先证 A 与 B 独立. 因为 A  AB  AB 且 (AB)(AB)  , 所以 P(A)  P(AB)  P(AB), 即 P(AB)  P(A) P(AB). , , . , , , 与 与 与 也相互独立 若 相互独立 则下列各对事件 A B A B A B 定理二 A B