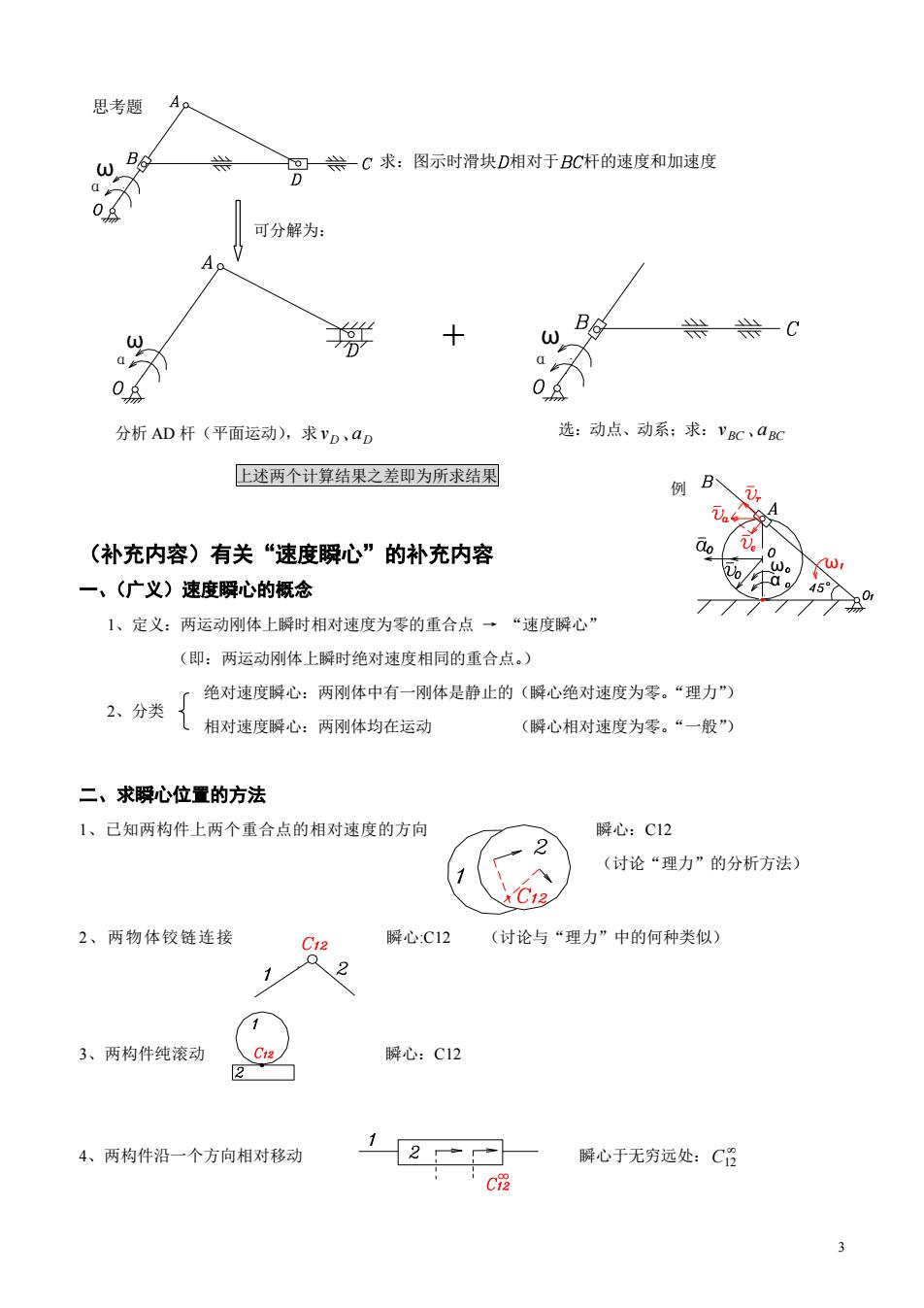
思考题 。C求：图示时滑块D相对于BC杆的速度和加速度 可分解为： 分析AD杆（平面运动），求VD,ap 选动点、动系：求：VC,aC 上述两个计算结果之差即为所求结果 例B (补充内容)有关“速度瞬心”的补充内容 一、（广义）速度瞬心的概念 1、定义：两运动刚体上瞬时相对速度为零的重合点一“速度瞬心” (即：两运动刚体上瞬时绝对速度相同的重合点。) 之、分类厂绝对速度厚心：两刚体中有-体是静止的（偶心绝对速度为零。“男力 儿相对速度瞬心：两刚体均在运动 (瞬心相对速度为零。“一般”) 二、求瞬心位置的方法 1、己知两构件上两个重合点的相对速度的方向 解心：C12 2 (讨论“理力”的分析方法》 ℃13 2、两物体铰链连接 C12 降心：C12 (讨论与“理力”中的何种类似) 1 、2 3、两构件纯滚动 瞬心：C12 2 4、两构件沿一个方向相对移动 12 解心于无穷远处：C日 3 ω α ω 例 上述两个计算结果之差即为所求结果 （补充内容）有关“速度瞬心”的补充内容 一、（广义）速度瞬心的概念 1、定义：两运动刚体上瞬时相对速度为零的重合点 → “速度瞬心” （即：两运动刚体上瞬时绝对速度相同的重合点。） 绝对速度瞬心：两刚体中有一刚体是静止的（瞬心绝对速度为零。“理力”） 相对速度瞬心：两刚体均在运动 （瞬心相对速度为零。“一般”） 二、求瞬心位置的方法 1、已知两构件上两个重合点的相对速度的方向 瞬心：C12 （讨论“理力”的分析方法） 2、两物体铰链连接 瞬心:C12 （讨论与“理力”中的何种类似） 3、两构件纯滚动 瞬心：C12 4、两构件沿一个方向相对移动 瞬心于无穷远处：  C12 思考题 ω α 求：图示时滑块 相对于 杆的速度和加速度 可分解为： α ω 分析 AD 杆（平面运动），求 D 、aD v ω α 选：动点、动系；求： BC 、aBC v + 2、分类