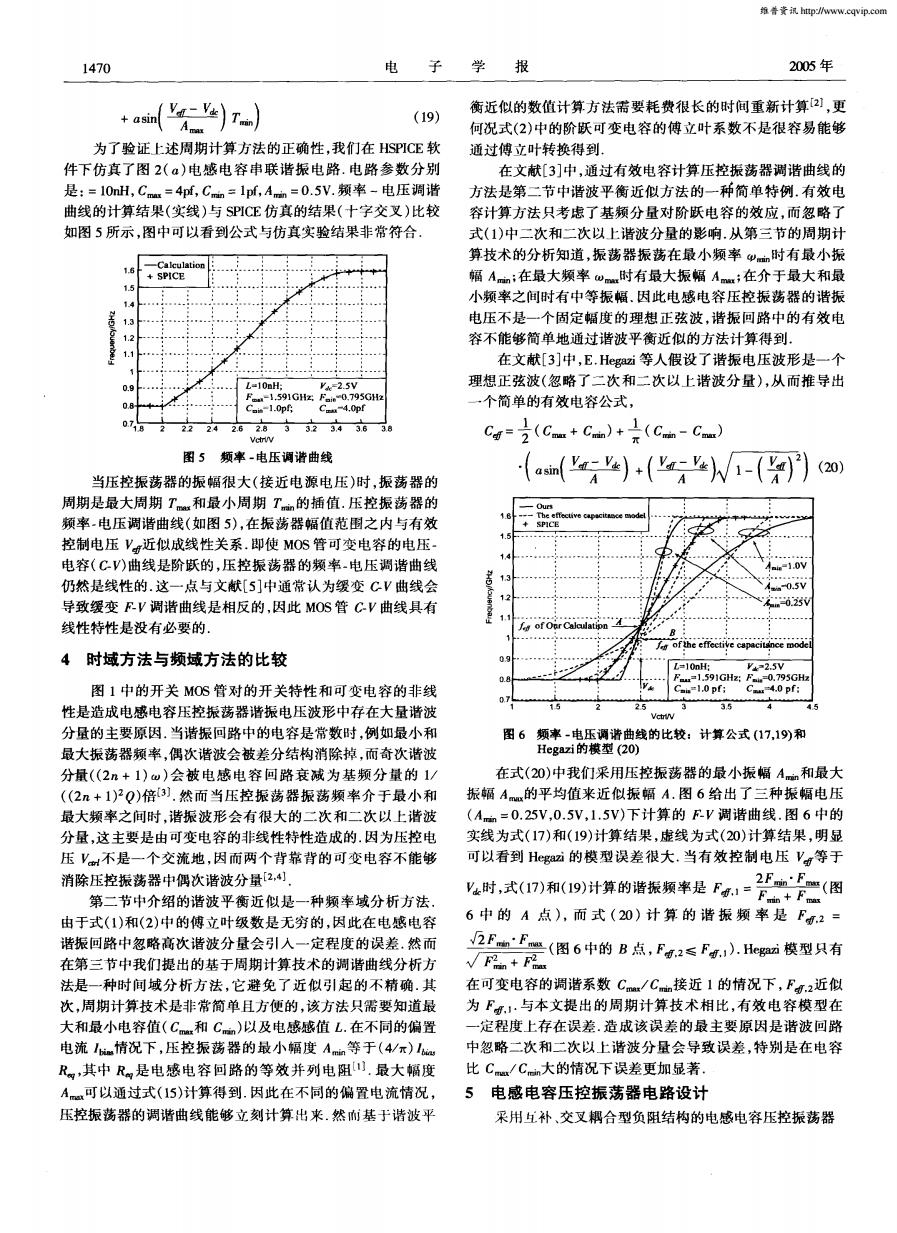
维告黄讯http://www,cqvip..com 1470 电 子 学 报 2005年 +）r 衡近似的数值计算方法需要耗费很长的时间重新计算2！，更 (19) 何况式(2)中的阶跃可变电容的傅立叶系数不是很容易能够 为了验证上述周期计算方法的正确性，我们在HSPICE软 通过傅立叶转换得到. 件下仿真了图2（α）电感电容串联谐振电路.电路参数分别 在文献[3]中，通过有效电容计算压控振荡器调谐曲线的 是：=10mH,Cmu=4pf,Cmn=1pf,Am=0.5V.频率-电压调谐 方法是第二节中谐波平衡近似方法的一种简单特例.有效电 曲线的计算结果（实线）与SPICE仿真的结果（十字交叉）比较 容计算方法只考虑了基频分量对阶跃电容的效应，而忽略了 如图5所示，图中可以看到公式与仿真实验结果非常符合 式(1)中二次和二次以上谐波分量的影响.从第三节的周期计 算技术的分析知道，振荡器振荡在最小频率wm时有最小振 1.6 SPICE 幅A:在最大频率wm时有最大振幅Am;在介于最大和最 1.4 小频率之间时有中等振幅.因此电感电容压控振荡器的谐振 1.3 电压不是一个固定幅度的理想正弦波，谐振回路中的有效电 1.2 容不能够简单地通过谐波平衡近似的方法计算得到. 1.1 在文献[3]中，E.Hegazi等人假设了谐振电压波形是一个 0.9 L=10nH; k-2.5V 理想正弦波（忽略了二次和二次以上谐波分量），从而推导出 F.-1.591GHx:F0.795GH2 0.8时 Csis-1.0pf C-4.0p 一个简单的有效电容公式， 0718 22 24 2.62.83 32343638 cg=2(cam+ca)+(ca-C） 图5频率-电压调谐曲线 (20 当压控振荡器的振幅很大（接近电源电压）时，振荡器的 asm'）+('W1-( 周期是最大周期T和最小周期T的插值.压控振荡器的 颍率.电压调谐曲线（如图5），在振荡器幅值范围之内与有效 SPICE 控制电压V近似成线性关系.即使MOS管可变电容的电压 电容(CV)曲线是阶跃的，压控振荡器的频率-电压调谐曲线 -1.0V 仍然是线性的.这一点与文献[5]中通常认为缓变CV曲线会 0.5V 导致缓变FV调谐曲线是相反的，因此MOS管CV曲线具有 线性特性是没有必要的」 of the effective capacitance mode 4时域方法与频域方法的比较 L=10nH: -2.5V F=1.591GHz:Fm=0.795GH 图1中的开关MOS管对的开关特性和可变电容的非线 Cai=1.0 pf: C4.0D: 性是造成电感电容压控振荡器谐振电压波形中存在大量谐波 25 3.5 Vctry 分量的主要原因.当谐振回路中的电容是常数时，例如最小和 图6频率-电压调谐曲线的比较：计算公式(17,19)和 最大振荡器频率，偶次谐波会被差分结构消除掉，而奇次谐波 Hegazi的模型(20) 分量(2n+1)w)会被电感电容回路衰减为基频分量的1/ 在式(20)中我们采用压控振荡器的最小振幅Am和最大 (2n+1)2Q)倍3).然而当压控振荡器振荡频率介于最小和 振幅Am的平均值来近似振幅A.图6给出了三种振幅电压 最大频率之间时，谐振波形会有很大的二次和二次以上谐波 (A=0.25V,0.5V,1.5V)下计算的E-V调谐曲线.图6中的 分量，这主要是由可变电容的非线性特性造成的.因为压控电 实线为式(17)和(19)计算结果，虚线为式(20)计算结果，明显 压V不是一个交流地，因而两个背靠背的可变电容不能够 可以看到Hegazi的模型误差很大.当有效控制电压Vg等于 消除压控振荡器中偶次谐波分量[2，， 2FnF(图 第二节中介绍的谐波平衡近似是一种频率域分析方法， y时，式(17)和(19)计算的谐振频率是F1=FF二 由于式(1)和(2)中的傅立叶级数是无穷的，因此在电感电容 6中的A点)，而式(20)计算的谐振频率是F.2= 谐振回路中忽略高次谐波分量会引入一定程度的误差.然而 2FF(图6中的B点，F2≤F,.Heg模型只有 在第三节中我们提出的基于周期计算技术的调谐曲线分析方 √F2n+F 法是一种时间域分析方法，它避免了近似引起的不精确.其 在可变电容的调谐系数Cm/Cm接近1的情况下，F.2近似 次，周期计算技术是非常简单且方便的，该方法只需要知道最 为F,1·与本文提出的周期计算技术相比，有效电容模型在 大和最小电容值(C和C)以及电感感值L.在不同的偏置 一定程度上存在误差.造成该误差的最主要原因是谐波回路 电流情况下，压控振荡器的最小幅度Am等于(4/r)lb 中忽略二次和二次以上谐波分量会导致误差，特别是在电容 R,其中R是电感电容回路的等效并列电阻.最大幅度 比Cmx/Cmn大的情况下误差更加显著。 A可以通过式(15)计算得到.因此在不同的偏置电流情况， 5电感电容压控振荡器电路设计 压控振荡器的调谐曲线能够立刻计算出来.然而基于谐波平 采用互补、交叉耦合型负阻结构的电感电容压控振荡器1470 电 子 学 报 2OO5矩 … in( ) ) (19) 为 了验证上述周期计算 方法的正确性 ，我们 在 HSPICE软 件下仿真 了图 2(a)电感 电容 串联 谐 振 电路 ．电路参 数 分别 是 ：=10nil，c～ =4pf，C =lpf，A,m =0．5V．频率 一电压 调谐 曲线 的计算结果 (实线 )与 SPICE仿真 的结果 (十字交叉 )比较 如图 5所示 ，图中可 以看到公式 与仿 真实 验结果非常符合 ． - CalculationI SPICE I L=10nH； _2 V ． 1．591GHz；F I。 795GHz _·_●一 Cml。=1．op C ．Opf V etrl／V 图 5 频率 ．电压调谐 曲线 当压控振荡器 的振 幅很大 (接 近电 源电压 )时 ，振荡 器的 周期是最大周期 7I眦 和最 小周 期 7 的插 值 ．压控 振荡 器的 频率 ．电压 调谐 曲线 (如 图 5)，在振荡器 幅值范 围之 内与有 效 控制电压 近似成线性关 系．即使 MOS管可变 电容的 电压 一 电容 (C-V)曲线是阶跃 的，压控 振荡器 的频率 一电压调谐 曲线 仍 然是 线性 的 ．这一点 与文 献[5]中通常认为缓变 C-V曲线会 导致缓变 F-V调谐 曲线 是相反的 ，因此 MOS管 C-V曲线具有 线 性特性是没有必要的 ． 4 时域方法与频域方法的比较 图 1中的开关 MOS管对 的开关特性 和 可变 电容 的非线 性是造成电感电容压控振荡器谐振电压波形中存在大量谐波 分量 的主要原因．当谐振 回路 中的电容是 常数 时 ，例如最小 和 最大振荡器频率 ，偶次谐波会被差分结构 消除掉 ，而奇次谐波 fitjr((2n+1) )会被 电感 电容 回路 衰减 为 基频 分 量 的 1／ ((2n+1)0p)倍[31．然 而 当压 控振 荡器 振 荡频率 介 于最 小和 最大频率之 间时 ，谐振 波形 会有 很大的 二次 和二次 以上谐波 分量 ，这 主要 是由可变 电容的非线性特性造成 的．因为压控 电 压 不 是一个 交流地 ，因而两 个背靠 背的 可变 电容 不能够 消除压控振荡器 中偶 次谐 波分 量Ll4J． 第二节 中介绍 的谐 波平衡近 似是 一种频 率域分 析方 法 ． 由于式 (1)和(2)中的傅 立叶级数 是无穷 的 ，因此在 电感 电容 谐振回路中忽略高次谐 波分量会 引入 一定程 度的误 差 ．然而 在第三节 中我们提 出的基 于周期计算技 术的调谐曲线分析方 法是一种 时 间域 分 析方 法 ，它避 免 了近似 引起 的不精 确 ．其 次 ，周期计算技术是非 常简单且 方便 的 ，该方 法只需要知道最 大和最小电容值(c～和 c )以及电感感值 ．在不同的偏置 电流 Jbi膻情况下 ，压 控 振荡 器 的最小 幅度 A 等 于 (4／ ) R棚，其中 R 是电感电容 回路的等效并列电阻_lj．最大幅度 A一可 以通过式(15)计算得 到．因此在 不同 的偏 置 电流情况 ， 压控振荡器 的调谐 曲线能够 立刻计 算 出来 ．然 mi基 于谐波 平 衡近似的数值计算方法需要耗费很长的时问重新计算 J，更 何况式 (2)中的阶跃可变 电容 的傅 立叶系数 不是很 容易能 够 通过傅 立叶转换得 到 ． 在文 献[3]中 ，通过有效 电容计算 压控振荡器调谐 曲线 的 方法是第二节中谐波平衡近似方法的一种简单特例．有效电 容计算方法 只考虑 了基频分 量对 阶跃 电容 的效应 ，而忽略 了 式 (1)中二 次和二次以上谐波分量的影响 ．从 第三节的周期计 算技术 的分析知道 ，振荡 器振 荡在最 小频 率 时有最 小振 幅 A ；在最 大频率 ct，一时有最大振幅 A～ ；在介于 最大和最 小频 率之间时有 中等振 幅 ．因此 电感 电容 压控振 荡器 的谐振 电压 不是一个 固定幅度 的理想 正弦 波 ，谐 振 回路中 的有 效 电 容不能够简单地通过谐 波平 衡近似的方法计算得到 ． 在文献 [3]中，E．Hegazi等人假设 了谐振 电压波形 是一个 理想正弦波(忽 略了二次 和二次 以上谐波 分量 )，从 而推 导 出 一 个简单的有效 电容公式 ， c =号(c～+c ) _=,It-(c 一c～) 。 (锄( )+( )√一())c加 图 6 频率 一电压调 谐 曲线的 比较 ：计算公式 (17，19)和 Hegazi的模 型 (2O) 在式 (20)中我们采用压控振荡器 的最 小振 幅 A 和最大 振 幅 A 的平均值来 近似振 幅 A．图 6给出 了三种 振幅 电压 (A =0．25V，0．5V，1．5V)下 计算 的 F-V调谐 曲线 ．图 6中的 实线 为式 (17)和(19)计算结 果 ，虚线 为式 (20)计算 结果 ，明显 可以看到 Hegazi的模 型误差 很 大．当有 效控 制 电压 等于 ，)F ．F 时 ，式(17)和 (19)计算 的谐振 频率是 ．。= (图 6中 的 A 点 )，而 式 (20)计 算 的 谐 振 频 率 是 ．2= "~ ／ F ． F ．I"min = I'max(图 6中的 B点 ， ， 2≤ ，1)．Hegazi模 型 只有 V ， + ，_眦 在可变 电容 的调谐 系数 ／C 接 近 1的情 况下 ， ．2近似 为 ．，．与本文提 出的周 期计 算技 术相 比，有 效 电容模 型 在 一 定程度上存在误差 ．造 成该误 差 的最 主要 原因是谐 波 回路 中忽略二次和二次 以上谐波 分量 会导致 误差 ，特别 是在 电容 比 c一／c 大 的情况下误差 更加 显著 ． 5 电感 电容压 控振 荡器 电路设计 采用互补 、交叉耦 合型负阻结构 的电感 电容压控振 荡器 N工0『^3u∞ 正 维普资讯 http://www.cqvip.com