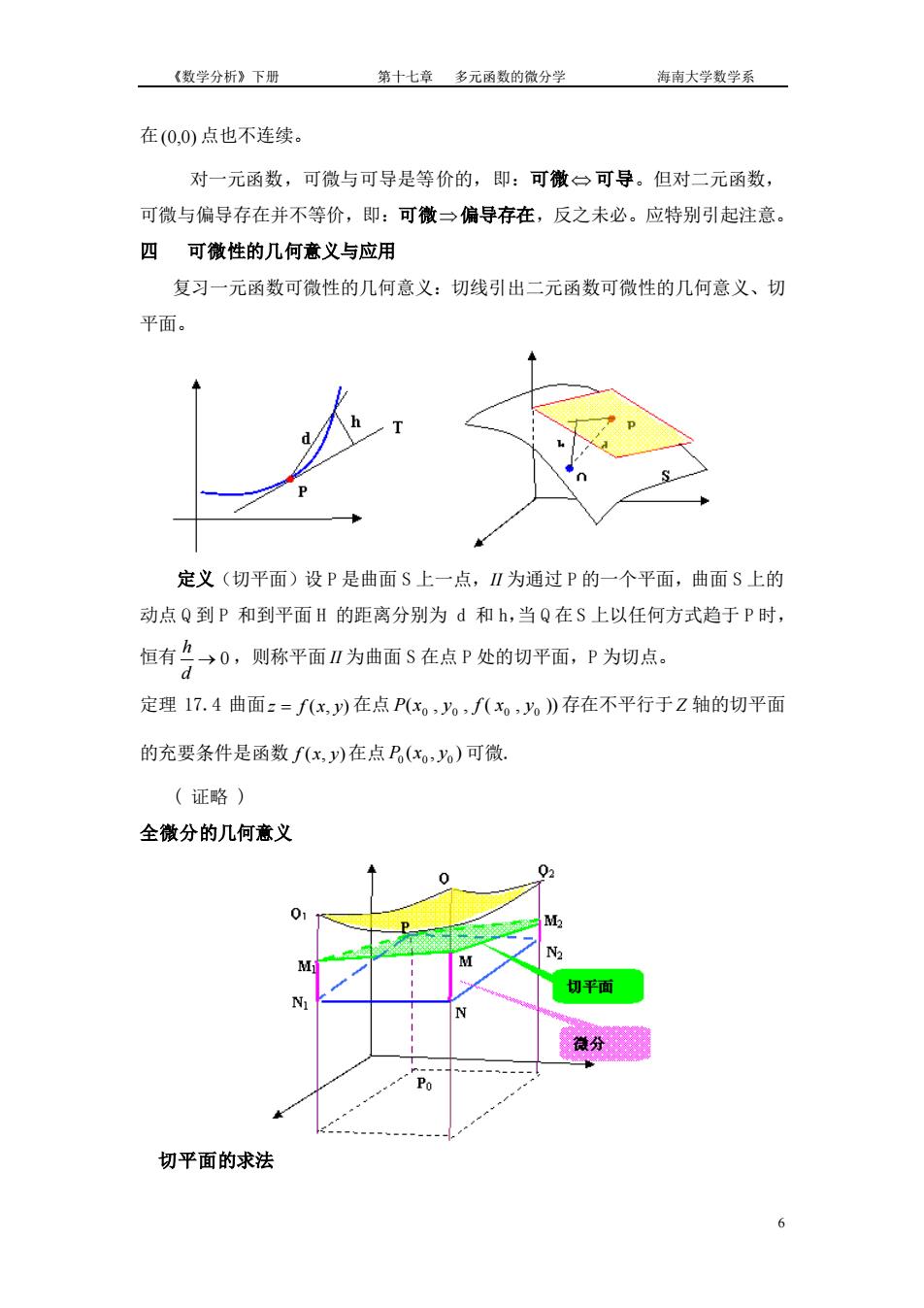
《数学分析》下册 第十七章多元函数的微分学 海南大学数学系 在(0,0)点也不连续。 对一元函数，可微与可导是等价的，即：可微一可导。但对二元函数， 可微与偏导存在并不等价，即：可微一偏导存在，反之未必。应特别引起注意 四可徽性的几何意义与应用 复习一元函数可微性的几何意义：切线引出二元函数可微性的几何意义、切 平面。 定义（切平面）设P是曲面S上一点，Ⅱ为通过P的一个平面，曲面S上的 动点Q到P和到平面H的距离分别为d和h,当Q在S上以任何方式趋于P时， 恒有么→0，则称平面Ⅱ为曲面S在点P处的切平面，P为切点. 定理17.4曲面：=fx,)在点P(x。,。,f(x。,》存在不平行于Z轴的切平面 的充要条件是函数f(x,y)在点P(xo,y%)可微. (证略) 全微分的几何意义 0 切平面 N. 分 切平面的求法《数学分析》下册 第十七章 多元函数的微分学 海南大学数学系 6 在 (0,0) 点也不连续。 对一元函数，可微与可导是等价的，即：可微  可导。但对二元函数， 可微与偏导存在并不等价，即：可微  偏导存在，反之未必。应特别引起注意。 四 可微性的几何意义与应用 复习一元函数可微性的几何意义：切线引出二元函数可微性的几何意义、切 平面。 定义（切平面）设 P 是曲面 S 上一点， II 为通过 P 的一个平面，曲面 S 上的 动点 Q 到 P 和到平面 H 的距离分别为 d 和 h，当 Q 在 S 上以任何方式趋于 P 时， 恒有 0 h d → ，则称平面 II 为曲面 S 在点 P 处的切平面，P 为切点。 定理 17.4 曲面 z = f (x, y) 在点 ( , , ( , )) 0 0 0 0 P x y f x y 存在不平行于 Z 轴的切平面 的充要条件是函数 f (x, y) 在点 ( , ) 0 0 0 P x y 可微. ( 证略 ) 全微分的几何意义 切平面的求法