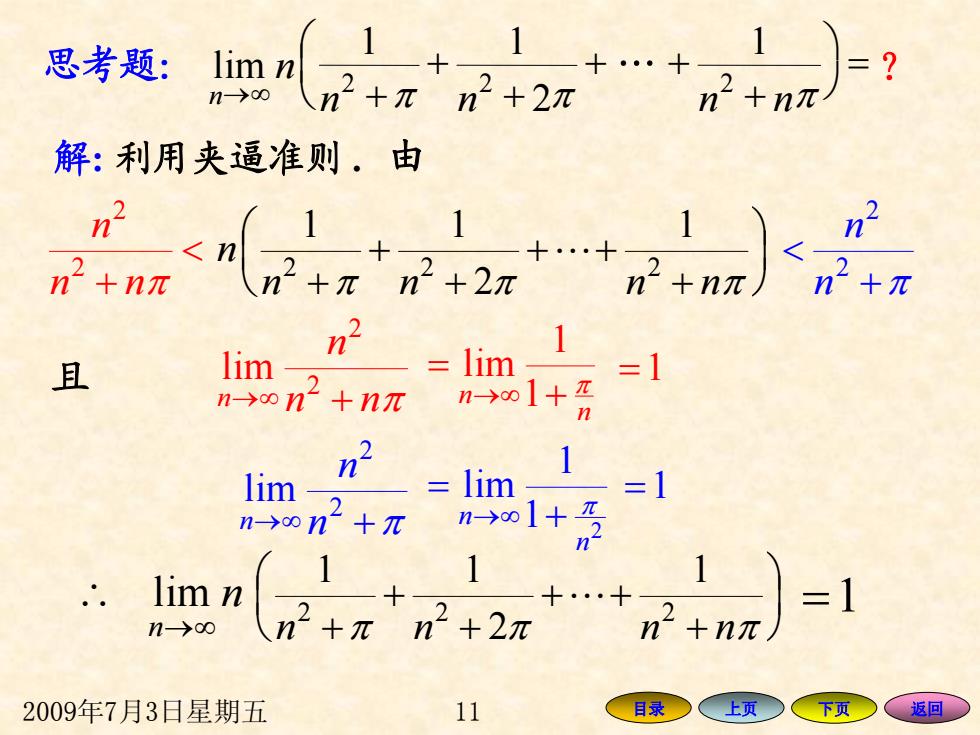
思考题： lim n n→o n2+元n2+2π =? 解：利用夹逼准则.由 n2 <n 1+ 1 1 n n2+nπ n+2π n2+n元) n2+π n2 且 lim-2 =lim =1 n-→on2+nπ n→∞1+ n 1 lim-2 lim. n→on2+π n 1 lim n 1=1 n->oo n2+π n2+2π n2+nx) 2009年7月3日星期五 11 目录 上页 下页 、返回一 2009年7月3日星期五 11 目录 上页 下页 返回 解 : 利用夹逼准则 . ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ++ + + + π nn π nn π n 2 2 2 1 2 11 < " + nn π n 2 2 + π < 2 2 n n 且 nn π n n ∞→ + 2 2 lim n n π + = ∞→ 1 1 lim = 1 ∞→ + π 2 2 lim n n n 2 1 1 lim n n π + = ∞→ = 1 n n ∞→ ∴ lim ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ++ + + + π nn π nn π 2 2 2 1 2 11 " = 1 由 思考题： ？ 1 2 11 lim 2 2 2 = ⎠ ⎞ ⎜ ⎝ ⎛ + ++ + + ∞→ + nn ππ nn π n n