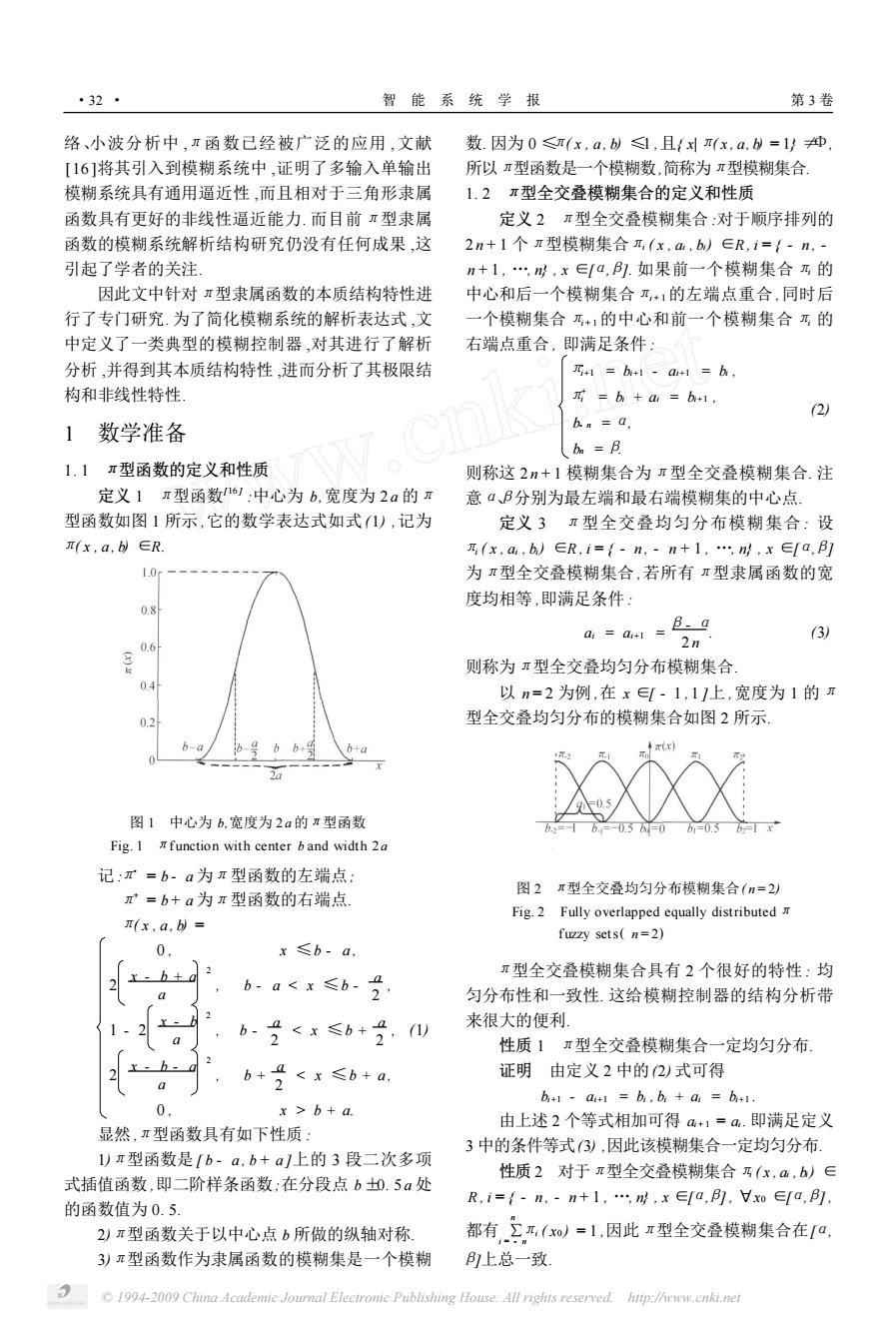
·32 智能系统学报 第3卷 络、小波分析中，Ⅱ函数已经被广泛的应用，文献 数.因为0≤π(x,a,bl,且{刘(x,a,b=1}绅 [16]将其引入到模糊系统中，证明了多输入单输出 所以π型函数是一个模糊数，简称为π型模糊集合 模糊系统具有通用逼近性，而且相对于三角形隶属 1.2π型全交叠模糊集合的定义和性质 函数具有更好的非线性逼近能力.而目前π型隶属 定义2π型全交叠模糊集合：对于顺序排列的 函数的模糊系统解析结构研究仍没有任何成果，这 2n+1个π型模糊集合元(x,a,b)∈R,i={-n,- 引起了学者的关注 n+1,,m,x∈[a,.如果前一个模糊集合乃的 因此文中针对π型隶属函数的本质结构特性进 中心和后一个模糊集合+1的左端点重合，同时后 行了专门研究.为了简化模糊系统的解析表达式，文 一个模糊集合乃+1的中心和前一个模糊集合乃的 中定义了一类典型的模糊控制器，对其进行了解析 右端点重合，即满足条件 分析，并得到其本质结构特性，进而分析了其极限结 r+1=b+l-a+1=b, 构和非线性特性 =b+a b1, 2) 1数学准备 b.n a ba=月 1.1π型函数的定义和性质 则称这2n+1模糊集合为π型全交叠模糊集合.注 定义1π型函数61：中心为b,宽度为2a的π 意aB分别为最左端和最右端模糊集的中心点. 型函数如图1所示，它的数学表达式如式1)，记为 定义3π型全交叠均匀分布模糊集合：设 r(x,a,b∈R 可(x,a,b)∈R,i=f-n,-n+1,n,x∈fa,] 1.0 为π型全交叠模糊集合，若所有π型隶属函数的宽 度均相等，即满足条件： 0.8 B.a a:=a+1= 3) 0.6 2n 则称为π型全交叠均匀分布模糊集合 0.4 以n=2为例，在x∈[-1,11上，宽度为1的π 0.2 型全交叠均匀分布的模糊集合如图2所示。 h+a 年元 2a 图1中心为b,宽度为2a的π型函数 03 Fig.I function with center b and width 2a 记：r=b-a为π型函数的左端点， π=b+a为π型函数的右端点 图2π型全交叠均匀分布模糊集合(n=2) Fig.2 Fully overlapped equally distributed (x,a,= fuzzy sets(n=2) 0 x≤b-a, π型全交叠模糊集合具有2个很好的特性：均 b-a<x≤b- 2 匀分布性和一致性.这给模糊控制器的结构分析带 a b-2 <x≤b+1 a 来很大的便利 21 1) 性质1π型全交叠模糊集合一定均匀分布. b+0 <x≤b+a 证明由定义2中的2)式可得 b+1-a+1=b,ba+a=b+1. 0 x b+a. 由上述2个等式相加可得a+1=a.即满足定义 显然，π型函数具有如下性质： 3中的条件等式3)，因此该模糊集合一定均匀分布. 1)π型函数是[b-a,b+a]上的3段二次多项 性质2对于π型全交叠模糊集合乃(x,a,b)∈ 式插值函数，即二阶样条函数：在分段点b0.5a处 R,i={-n,-n+1,,n,x∈Ia,1,Vxo∈a,] 的函数值为0.5. 2)π型函数关于以中心点b所做的纵轴对称 都有，工严，(o)=1,因此r型全交叠模糊集合在a, 3)π型函数作为隶属函数的模糊集是一个模糊 上总一致 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved. http://www.cnki.net络、小波分析中 ,π函数已经被广泛的应用 ,文献 [16 ]将其引入到模糊系统中 ,证明了多输入单输出 模糊系统具有通用逼近性 ,而且相对于三角形隶属 函数具有更好的非线性逼近能力. 而目前π型隶属 函数的模糊系统解析结构研究仍没有任何成果 ,这 引起了学者的关注. 因此文中针对π型隶属函数的本质结构特性进 行了专门研究. 为了简化模糊系统的解析表达式 ,文 中定义了一类典型的模糊控制器 ,对其进行了解析 分析 ,并得到其本质结构特性 ,进而分析了其极限结 构和非线性特性. 1 数学准备 1. 1 π型函数的定义和性质 定义 1 π型函数[16 ] :中心为 b,宽度为 2 a 的π 型函数如图 1 所示 ,它的数学表达式如式 (1) ,记为 π( x , a , b) ∈R. 图 1 中心为 b,宽度为 2 a 的π型函数 Fig. 1 πfunction with center b and width 2 a 记 :π- = b - a 为π型函数的左端点; π+ = b + a 为π型函数的右端点. π( x , a , b) = 0 , x ≤b - a , 2 x - b + a a 2 , b - a < x ≤b - a 2 , 1 - 2 x - b a 2 , b - a 2 < x ≤b + a 2 , 2 x - b - a a 2 , b + a 2 < x ≤b + a , 0 , x > b + a. (1) 显然 ,π型函数具有如下性质 : 1)π型函数是[ b - a , b + a ]上的 3 段二次多项 式插值函数 ,即二阶样条函数;在分段点 b±0. 5 a 处 的函数值为 0. 5. 2)π型函数关于以中心点 b 所做的纵轴对称. 3)π型函数作为隶属函数的模糊集是一个模糊 数. 因为 0 ≤π( x , a , b) ≤1 ,且{ x|π( x , a, b) = 1} ≠Φ, 所以π型函数是一个模糊数,简称为π型模糊集合. 1. 2 π型全交叠模糊集合的定义和性质 定义 2 π型全交叠模糊集合 :对于顺序排列的 2 n + 1 个π型模糊集合πi ( x , ai , bi) ∈R , i = { - n , - n + 1 , …, n} , x ∈[α,β]. 如果前一个模糊集合πi 的 中心和后一个模糊集合πi + 1 的左端点重合 ,同时后 一个模糊集合πi + 1 的中心和前一个模糊集合πi 的 右端点重合 , 即满足条件 : π- i+1 = bi+1 - ai+1 = bi , π+ i = bi + ai = bi+1 , b- n =α, bn =β. (2) 则称这 2 n + 1 模糊集合为π型全交叠模糊集合. 注 意α、β分别为最左端和最右端模糊集的中心点. 定义 3 π型全交叠均匀分布模糊集合 : 设 πi ( x , ai , bi) ∈R , i = { - n , - n + 1 , …, n} , x ∈[α,β] 为π型全交叠模糊集合 ,若所有π型隶属函数的宽 度均相等 ,即满足条件 : ai = ai+1 = β- α 2 n . (3) 则称为π型全交叠均匀分布模糊集合. 以 n = 2 为例 ,在 x ∈[ - 1 , 1 ]上 ,宽度为 1 的π 型全交叠均匀分布的模糊集合如图 2 所示. 图 2 π型全交叠均匀分布模糊集合( n = 2) Fig. 2 Fully overlapped equally distributedπ fuzzy sets( n = 2) π型全交叠模糊集合具有 2 个很好的特性 : 均 匀分布性和一致性. 这给模糊控制器的结构分析带 来很大的便利. 性质 1 π型全交叠模糊集合一定均匀分布. 证明 由定义 2 中的(2) 式可得 bi+1 - ai+1 = bi , bi + ai = bi+1 . 由上述 2 个等式相加可得 ai + 1 = ai . 即满足定义 3 中的条件等式(3) ,因此该模糊集合一定均匀分布. 性质 2 对于π型全交叠模糊集合πi ( x , ai , bi) ∈ R , i = { - n , - n + 1 , …, n} , x ∈[α,β] , Πx0 ∈[α,β] , 都有 ∑ n i = - n πi ( x0 ) = 1 ,因此π型全交叠模糊集合在[α, β]上总一致. ·32 · 智 能 系 统 学 报 第 3 卷 © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net