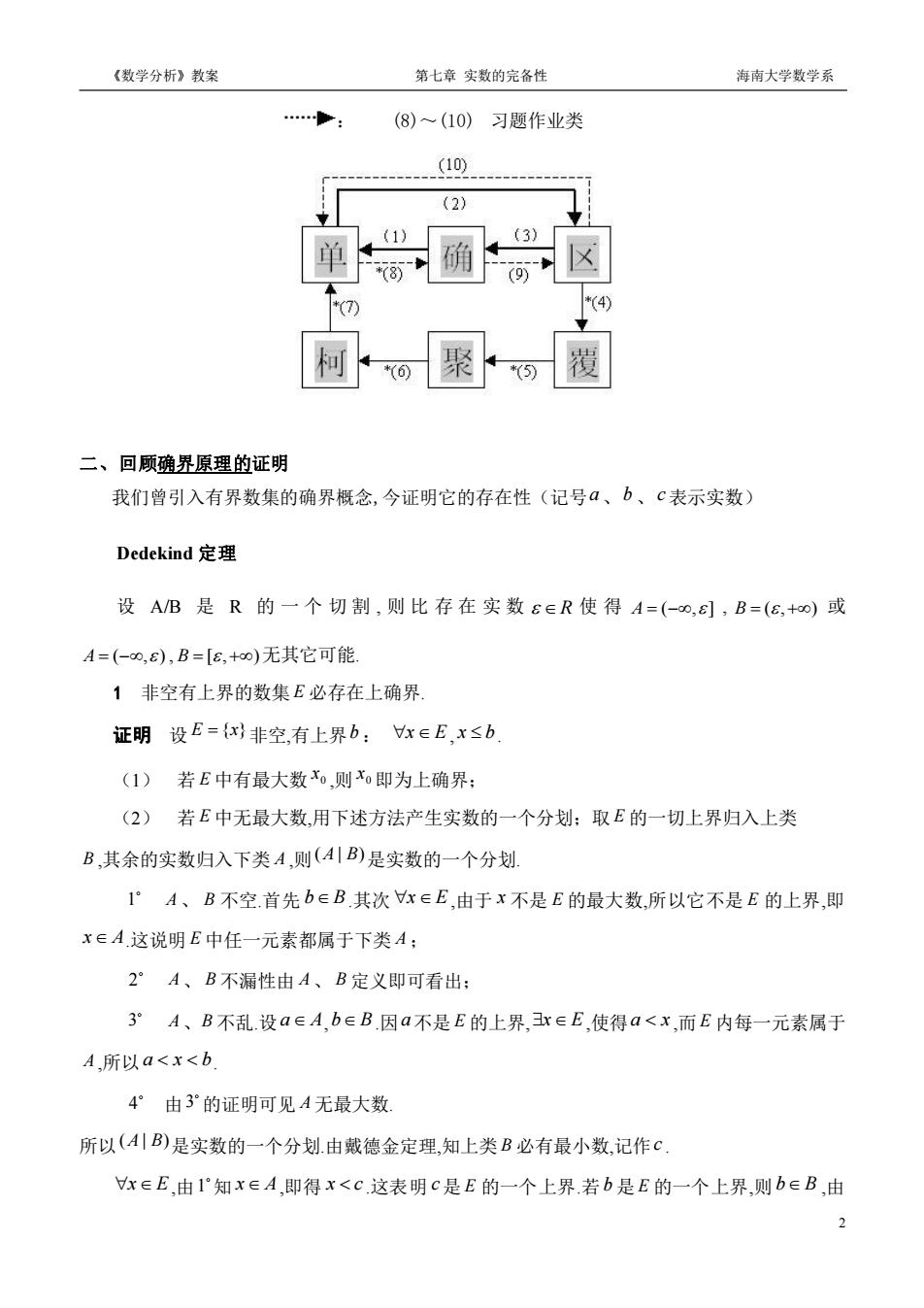
《数学分析》教案 第七章实数的完备性 海南大学数学系 (8)~(10)习题作业类 .-(10 (2 柯o聚o覆 二、回顾确界原理的证明 我们曾引入有界数集的确界概念，今证明它的存在性（记号a、b、c表示实数） Dedekind定理 设AB是R的一个切割，则比存在实数E∈R使得A=(-o,),B=(8,+o)或 A=(-o,s),B=【8,+o)无其它可能. 1非空有上界的数集￡必存在上确界 证明设E={x非空，有上界b:x∈E,x≤b (1)若E中有最大数x,则x即为上确界： (2)若E中无最大数，用下述方法产生实数的一个分划：取E的一切上界归入上类 B,其余的实数归入下类A,则(4B)是实数的一个分划！ 1°A、B不空首先bEB其次r∈E,由于x不是E的最大数，所以它不是E的上界，即 xEA这说明E中任一元素都属于下类A; 2°A、B不漏性由A、B定义即可看出： 3°A、B不乱.设aeA,b∈B.因a不是E的上界，3r∈E,使得a<x,而E内每一元素属于 A,所以a<x<b 4°由3°的证明可见A无最大数 所以(4川B)是实数的一个分划.由戴德金定理，知上类B必有最小数，记作C x∈E,由1“知x∈A,即得x<c这表明c是E的一个上界.若b是E的一个上界，则b∈B,由 2《数学分析》教案 第七章 实数的完备性 海南大学数学系 2 ： (8)～(10) 习题作业类 二、回顾确界原理的证明 我们曾引入有界数集的确界概念,今证明它的存在性（记号 a、b 、c 表示实数） Dedekind 定理 设 A/B 是 R 的 一 个 切 割 , 则 比 存 在 实 数  R 使 得 A = − ( , ]  , B = + ( , )  或 A = − ( , )  , B = + [ , )  无其它可能. 1 非空有上界的数集 E 必存在上确界. 证明 设 E = {x} 非空,有上界 b ： x E, x  b. （1） 若 E 中有最大数 0 x ,则 0 x 即为上确界； （2） 若 E 中无最大数,用下述方法产生实数的一个分划；取 E 的一切上界归入上类 B ,其余的实数归入下类 A ,则 (A | B) 是实数的一个分划.  1 A、 B 不空.首先 bB.其次 x E,由于 x 不是 E 的最大数,所以它不是 E 的上界,即 x A.这说明 E 中任一元素都属于下类 A ；  2 A、 B 不漏性由 A 、 B 定义即可看出；  3 A、B 不乱.设 a A,bB.因 a 不是 E 的上界,xE,使得 a  x ,而 E 内每一元素属于 A ,所以 a  x  b.  4 由  3 的证明可见 A 无最大数. 所以 (A | B) 是实数的一个分划.由戴德金定理,知上类 B 必有最小数,记作 c . x E,由  1 知 x A,即得 x  c .这表明 c 是 E 的一个上界.若 b 是 E 的一个上界,则 bB ,由