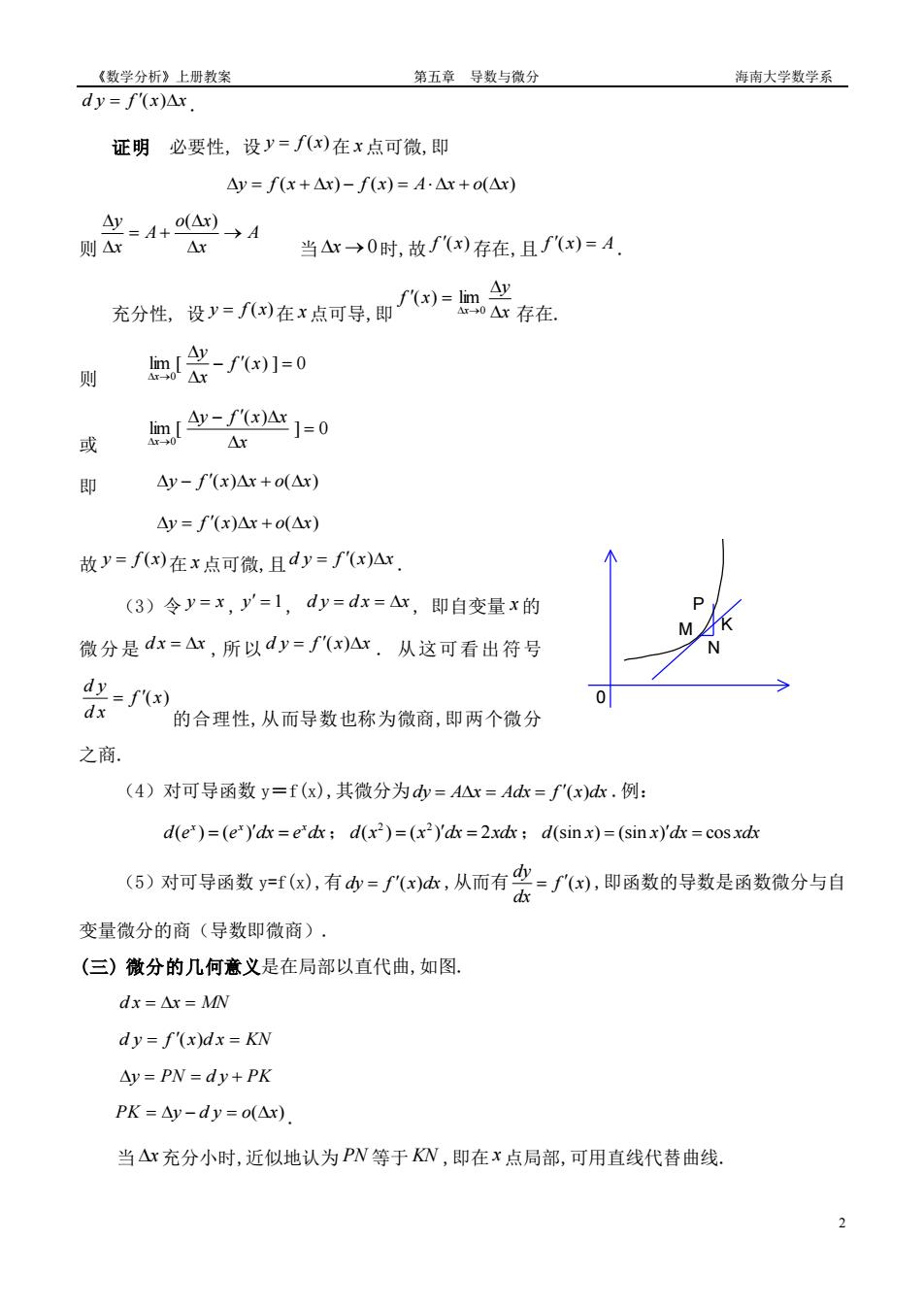
《数学分析》上册教案 第五章导数与微分 海南大学数学系 dy=f(x)Ax. 证明必要性，设y=)在x点可微，即 △y=fx+△x)-f(x)=A△r+o(△x) 则是-4+→4 Ax 当△x→0时，故f"(x)存在，且f(x)=A. 充分性设=回在点可导，即四血品存在 则 -兴-fx1=0 或 -山1=0 △r 即 △y-f'(x)Ar+o(Ax) △y=f'(x)Ax+o(△x) 故y=f)在x点可微，且d=fx)Ar (3)令y=x,y=1,dy=dx=△r,即自变量x的 微分是dr=△r,所以dy=f'(x)△r.从这可看出符号 器 的合理性，从而导数也称为微商，即两个微分 之商. (4)对可导函数y=f(x),其微分为=A△r=Ad:=f(x)k.例： d(e)=(e")'dx=e'dx:d(x2)=(x2)'dx=2xdx:d(sinx)=(sinx)'dx cosxdx (5)对可导函数y=fx),有少=了x)冰，从而有血=f,即函数的导数是函数微分与自 dx 变量微分的商（导数即微商）· (三)微分的几何意义是在局部以直代曲，如图。 dx=△r=MN dy=f'(x)dx=KN △y=PN=dy+PK PK=△y-dy=o(△x) 当△x充分小时，近似地认为PW等于K,即在x点局部，可用直线代替曲线.《数学分析》上册教案 第五章 导数与微分 海南大学数学系 2 d y = f (x)x . 证明 必要性, 设 y = f (x) 在 x 点可微,即 y = f (x + x) − f (x) = Ax + o(x) 则 A x o x A x y →   = +   ( ) 当 x →0 时,故 f (x) 存在,且 f (x) = A . 充分性, 设 y = f (x) 在 x 点可导,即 x y f x x    =  →0 ( ) lim 存在. 则 lim [ ( ) ] 0 0 −  =    → f x x y x 或 ] 0 ( ) lim [ 0 =   −    → x y f x x x 即 y − f (x)x + o(x) y = f (x)x + o(x) 故 y = f (x) 在 x 点可微,且 d y = f (x)x . （3）令 y = x , y = 1 , d y = d x = x , 即自变量 x 的 微分是 d x = x ,所以 d y = f (x)x . 从这可看出符号 f (x) d x d y =  的合理性,从而导数也称为微商,即两个微分 之商. （4）对可导函数 y＝f(x),其微分为 dy A x Adx f x dx =  = = ( ) .例： ( ) ( ) x x x d e e dx e dx = =  ； 2 2 d x x dx xdx ( ) ( ) 2 = =  ； d x x dx xdx (sin ) (sin ) cos = =  （5）对可导函数 y=f(x),有 dy f x dx = ( ) ,从而有 ( ) dy f x dx =  ,即函数的导数是函数微分与自 变量微分的商（导数即微商）. (三) 微分的几何意义是在局部以直代曲,如图. d x = x = MN d y = f (x)d x = KN y = PN = d y + PK PK = y − d y = o(x) . 当 x 充分小时,近似地认为 PN 等于 KN ,即在 x 点局部,可用直线代替曲线. 0 M N K P