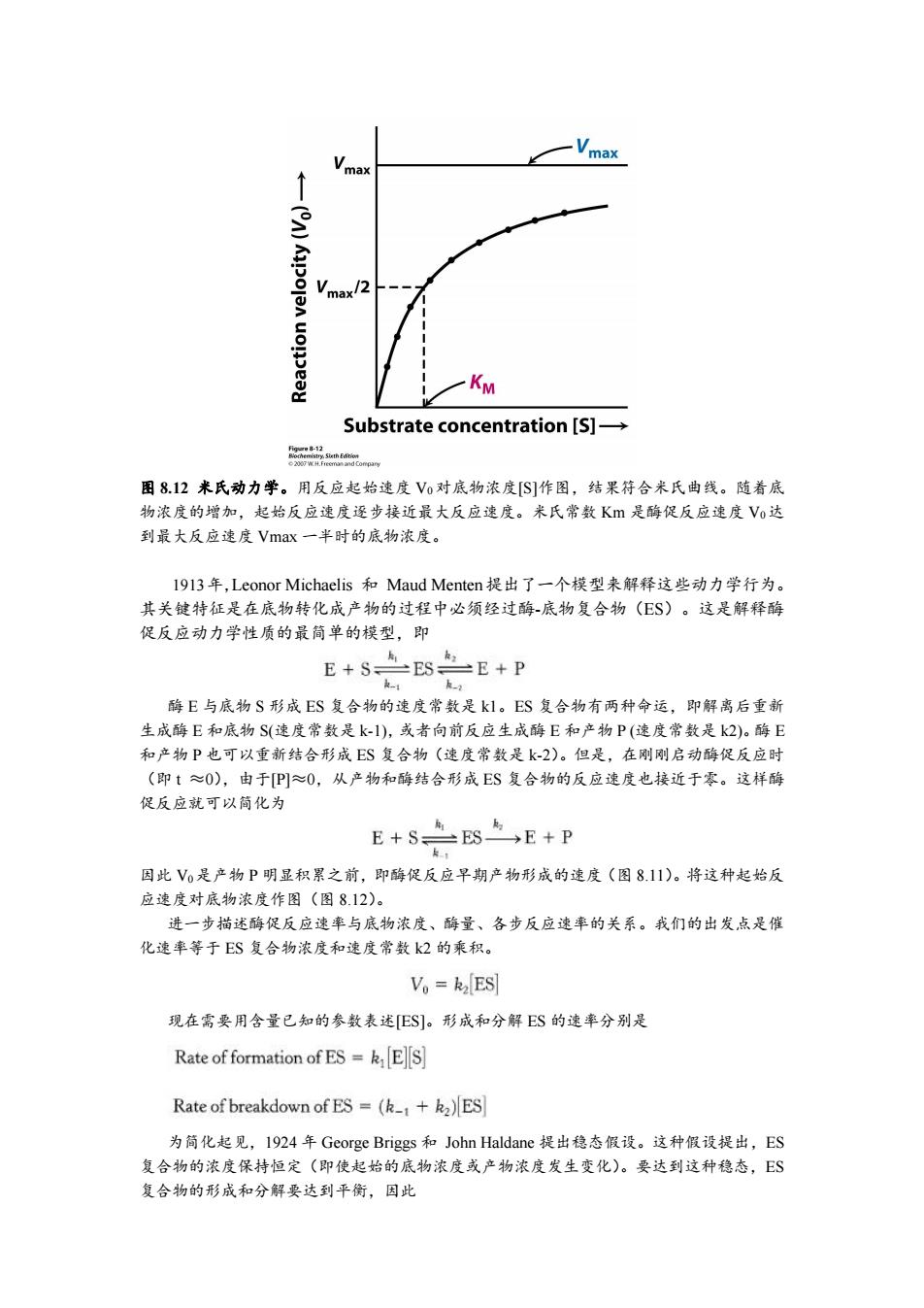
Vma Vmax Vmax/2 Substrate concentration [S]- 42 28faopaw 图812米氏动力学。用反应起始速度V0对底物浓度[S]作图，结果符合米氏曲线。随着底 物浓度的增加，起始反应速度逐步接近最大反应速度。米氏常数K是酶促反应速度Vo达 到最大反应速度Vmax一半时的底物浓度。 I9l3年，Leonor Michaelis和Maud Menten提出了一个模型来解释这些动力学行为。 其关镀特征是在底物转化成产物的过程中必须经过酶-底物复合物(ES)。这是解释酶 促反应动力学性质的最简单的模型，即 E+S点SE+P k-1 酶E与底物S形成ES复合物的速度常数是k1。ES复合物有两种命运，即解离后重新 生成酶E和底物S(速度常数是k-1),或者向前反应生成酶E和产物P(速度常数是k2)。酶E 和产物P也可以重新结合形成ES复合物（速度常数是k-2)。但是，在刚刚启动酶促反应时 (即t≈0)，由于P]≈0，从产物和酶结合形成ES复合物的反应速度也接近于零。这样酶 促反应就可以简化为 E+S焦S与E+P R 因此Vo是产物P明显积累之前，即酶促反应早期产物形成的速度（图8.11）。将这种起始反 应速度对底物浓度作图（图8.12）。 进一步描述酶促反应速率与底物浓度、酶量、各步反应速率的关系。我们的出发点是催 化速率等于ES复合物浓度和速度常数k2的乘积。 V。=k2ES 现在需要用含量已知的参数表述[ES]。形成和分解ES的速率分别是 Rate of formation of ES=k E]S] Rate of breakdown of ES =(k_+k2)ES 为简化起见，1924年George Briggs和John Haldane提出稳态假设。这种假设提出，ES 复合物的浓度保持恒定（即使起始的底物浓度或产物浓度发生变化）。要达到这种稳态，ES 复合物的形成和分解要达到平衡，因此图 8.12 米氏动力学。用反应起始速度 V0 对底物浓度[S]作图，结果符合米氏曲线。随着底 物浓度的增加，起始反应速度逐步接近最大反应速度。米氏常数 Km 是酶促反应速度 V0达 到最大反应速度 Vmax 一半时的底物浓度。 1913年，Leonor Michaelis 和 Maud Menten提出了一个模型来解释这些动力学行为。 其关键特征是在底物转化成产物的过程中必须经过酶-底物复合物（ES）。这是解释酶 促反应动力学性质的最简单的模型，即 酶 E 与底物 S 形成 ES 复合物的速度常数是 k1。ES 复合物有两种命运，即解离后重新 生成酶 E 和底物 S(速度常数是 k-1)，或者向前反应生成酶 E 和产物 P (速度常数是 k2)。酶 E 和产物 P 也可以重新结合形成 ES 复合物（速度常数是 k-2）。但是，在刚刚启动酶促反应时 （即 t ≈0），由于[P]≈0，从产物和酶结合形成 ES 复合物的反应速度也接近于零。这样酶 促反应就可以简化为 因此 V0是产物 P 明显积累之前，即酶促反应早期产物形成的速度（图 8.11）。将这种起始反 应速度对底物浓度作图（图 8.12）。 进一步描述酶促反应速率与底物浓度、酶量、各步反应速率的关系。我们的出发点是催 化速率等于 ES 复合物浓度和速度常数 k2 的乘积。 现在需要用含量已知的参数表述[ES]。形成和分解 ES 的速率分别是 为简化起见，1924 年 George Briggs 和 John Haldane 提出稳态假设。这种假设提出，ES 复合物的浓度保持恒定（即使起始的底物浓度或产物浓度发生变化）。要达到这种稳态，ES 复合物的形成和分解要达到平衡，因此