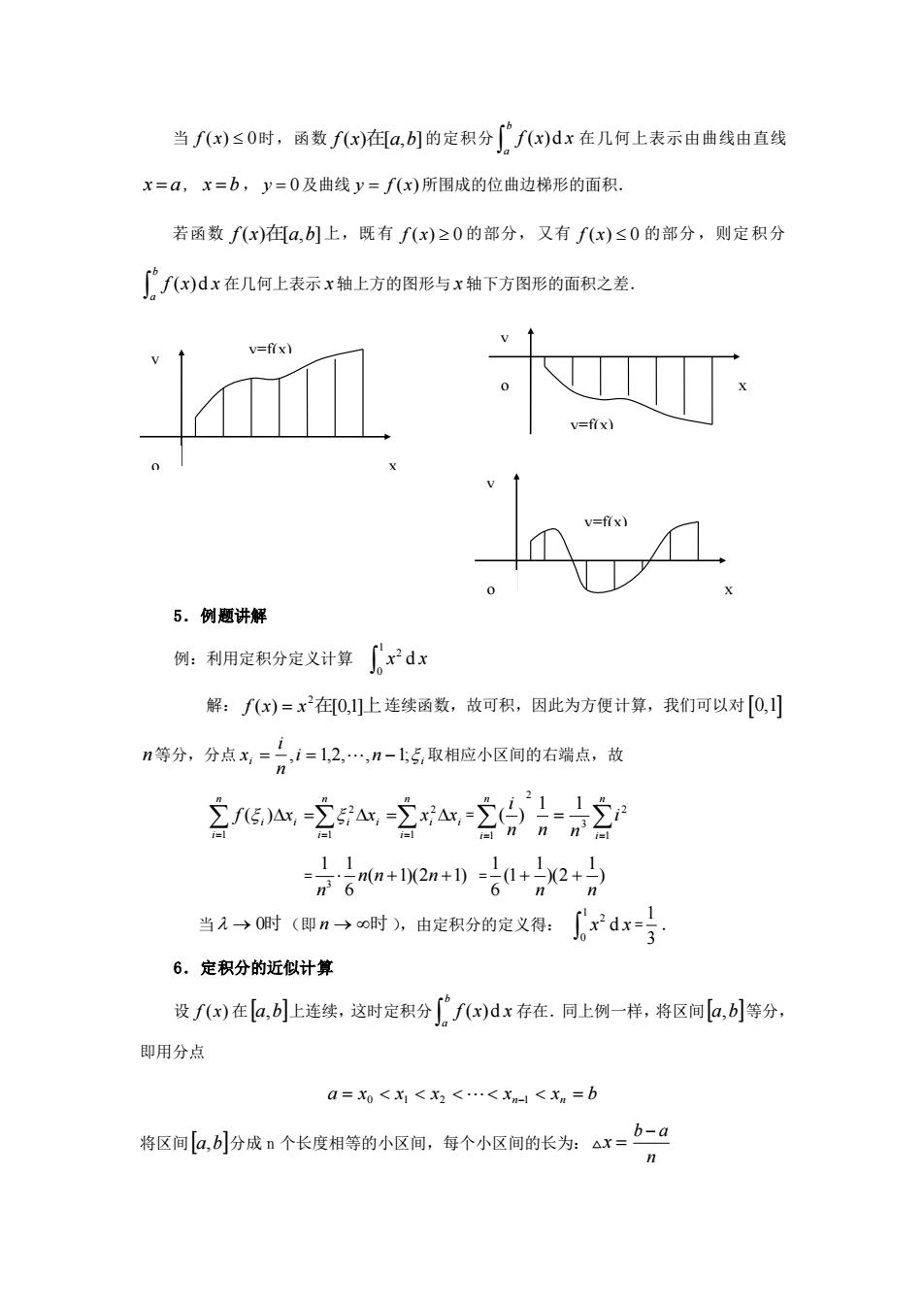
当fx)≤0时，函数fx)在a,的定积分[fx)dx在几何上表示由曲线由直线 x=a,x=b,y=0及曲线y=fx)所围成的位曲边梯形的面积 若函数f(x)a,b]上，既有f(x)≥0的部分，又有f(x)≤0的部分，则定积分 ∫f(x)dx在几何上表示x轴上方的图形与x轴下方图形的面积之差， v↑ v=fix =frx) v=f7x) 5.例题讲解 例：利用定积分定义计算[x2dx 解：fx)=x在0，止连续函数，故可积，因此为方便计算，我们可以对[0， n等分，分点x,=。i=12,.,1-上5，取相应小区间的右端点，故 5宫9- 名a+2m+)0+x2+的 当无→0时（即n→时），由定积分的定义得：rdx背 6.定积分的近似计算 设f(x)在[a,b上连续，这时定积分f(x)dx存在.同上例一样，将区间a,b等分， 即用分点 a=0<x<3<.<x<xn=b 将区间血，小分成n个长度相等的小区间，每个小区间的长为△x=-口 当 f x( ) 0  时，函数 f (x)在[a,b] 的定积分 ( )d b a f x x  在几何上表示由曲线由直线 x a = , x b = ， y = 0 及曲线 y = f (x) 所围成的位曲边梯形的面积． 若函数 f (x)在[a,b] 上，既有 f x( ) 0  的部分，又有 f x( ) 0  的部分，则定积分 ( )d b a f x x  在几何上表示 x 轴上方的图形与 x 轴下方图形的面积之差． 5．例题讲解 例：利用定积分定义计算 1 2 0 x x d  解： f (x) = x 2在[0,1]上 连续函数，故可积，因此为方便计算，我们可以对 0,1 n 等分，分点 i n i i n i x = , = 1,2,, −1; 取相应小区间的右端点，故    = = =  =  =  n i i i n i i i n i i i f x x x x 1 2 1 2 1 ( )  =  = = = n i n i i n n n i 1 2 3 2 1 1 1 ( ) = 3 1 1 ( 1)(2 1) 6 n n n n  + + = ) 1 )(2 1 (1 6 1 n n + + 当  → 0时 （即 n → 时 ），由定积分的定义得： 1 2 0 x x d  = 3 1 ． 6．定积分的近似计算 设 f (x) 在 a,b 上连续，这时定积分 ( )d b a f x x  存在．同上例一样，将区间 a,b 等分， 即用分点 a = x0  x1  x2  xn−1  xn = b 将区间 a,b 分成 n 个长度相等的小区间，每个小区间的长为： x = b a n − y=f(x) o x y o x y y=f(x) y=f(x) o x y