
第五章定积分 一、学时分配: 讲课学时:10习题课学时:2 共12学时 二、基本内容: 1.定积分的概念与性质: 2.微积分基木公式: 5.反常积分的审敛法与「函数。 三、教学要求: 1.理解定积分、反常积分和厂函数的概念及相关性质: 四、重点难点 1.重点:定积分、反常积分和Γ函数的概念:微积分的基本公式以及定积分的换元法 和分部积分法. 2.难点:定积分、反常积分和「函数的相关性质:变动上限的函数的应用:利用微积 分的基本公式以及定积分的换元法和分部积分法求解定积分与反常积分:利 用反常积分的审敛法判断反常积分的敛散性 第一节定积分的概念与性质 教学目的: 1.通过实际问题的引入,使学生理解和掌握定积分的定义与性质: 2.了解定积分的几何意义,能用定积分的定义计算简单的定积分: 3.利用定积分的性质解决估值、证明等相关问题.。 教学重点:定积分的定义. 教学难点:定积分的性质的应用(特别是中值定理). 教学过程: 一、定积分问题举例: 1.曲边梯形的面积 (1)曲边梯形的概念:设y=f(x)在[a,b]上非负,连续.由直线x=a,x=b,y=0 及曲线y=f(x)所围成的图形ABCD称为曲边梯形,其中曲线弧称为曲边 (2)曲边梯形面积的求解 在区间[a,b]中任意插入若干个分点 a=0<x<3<x<xn=b, 把a,b分成n个小区间
第五章 定积分 一、学时分配: 讲课学时:10 习题课学时:2 共 12 学时 二、基本内容: 1.定积分的概念与性质; 2.微积分基本公式; 3.定积分的换元法和分部积分法; 4.反常积分; 5.反常积分的审敛法与 函数. 三、教学要求: 1.理解定积分、反常积分和 函数的概念及相关性质; 2.掌握微积分的基本公式,会利用定积分的换元法和分部积分法求解定积分; 3.掌握反常积分的求解方法,能利用反常积分的审敛法判断反常积分的敛散性. 四、重点难点 1.重点:定积分、反常积分和 函数的概念;微积分的基本公式以及定积分的换元法 和分部积分法. 2.难点:定积分、反常积分和 函数的相关性质;变动上限的函数的应用;利用微积 分的基本公式以及定积分的换元法和分部积分法求解定积分与反常积分;利 用反常积分的审敛法判断反常积分的敛散性. 第一节 定积分的概念与性质 教学目的: 1. 通过实际问题的引入,使学生理解和掌握定积分的定义与性质; 2. 了解定积分的几何意义,能用定积分的定义计算简单的定积分; 3. 利用定积分的性质解决估值、证明等相关问题. 教学重点:定积分的定义. 教学难点:定积分的性质的应用(特别是中值定理). 教学过程: 一、定积分问题举例: 1.曲边梯形的面积 (1)曲边梯形的概念:设 y = f (x) 在 a,b 上非负,连续.由直线 x a = , x b = ,y = 0 及曲线 y = f (x) 所围成的图形 ABCD 称为曲边梯形,其中曲线弧称为曲边. (2)曲边梯形面积的求解 在区间 a,b 中任意插入若干个分点 a = x0 x1 x2 xn−1 xn = b , 把 a,b 分成 n 个小区间 D x o A B C y

[xo][x],[xx] 它们的长度依次为: △x1=x-x0,△x2=x2-x,.,△xn=xn-xn 经过每一个分点作平行于x轴的直线段,把曲边梯形分成n个窄曲边梯形,在每个小区 间[x1x,]上任取一点5:,以[x1,x,]为底,f(5)为高的窄矩形近似替代第i个窄边梯 形(1=1,2,.,n),把这样得到的n个窄矩形面积之和作为所求曲边梯形面积A的近似值, 即 A≈f(5)△x1+f5)△x2+.+f(5n)△x。 =∑f5,)A 设=max{△x1,△x2,.△xn}→0时(这时分段数n无限增多,即n→0),取 上述和式的极限,便得曲边梯形的面积 A=∑fGAx 2.变速直线运动的略程 (1)问题提出:设某物体作直线运动,已知速度v=()是时间间隔[T,T,]上1的连 续函数,且)≥0,计算在这段时间内物体所经过的路程。 (2)解决过程: 在[工,工]内任意插入若干个分点 T=10<1<h2<1n<1n=T2, 把[T,T]分成n个小段 [o],[t,l2],[n1n]。 各小段时间的长依次为: =14-6,△M2=4-4,.,△1n=n-11 相应各段时间内物体经过的路程为:
[ 0 1 x , x ],[ 1 2 x , x ], . [ n n x , x −1 ], 它们的长度依次为: 1 1 0 2 2 1 1 , , , = − = − n = n − n− x x x x x x x x x 经过每一个分点作平行于 x 轴的直线段,把曲边梯形分成 n 个窄曲边梯形,在每个小区 间[ i i x , x −1 ]上任取一点 i ,以[ i i x , x −1 ]为底, ( ) i f 为高的窄矩形近似替代第 i 个窄边梯 形( i n =1, 2, , ),把这样得到的 n 个窄矩形面积之和作为所求曲边梯形面积 A 的近似值, 即 i n n A f ( )x + f ( )x + + f ( )x 1 2 2 = = n i i i f x 1 ( ) 设 = maxx1 ,x2 , xn , → 0 时(这时分段数 n 无限增多,即 n → ),取 上述和式的极限,便得曲边梯形的面积 = → = n i i i A A f x 1 0 lim ( ) 2.变速直线运动的路程 (1)问题提出:设某物体作直线运动,已知速度 v = v(t) 是时间间隔[ 1 2 T ,T ]上 t 的连 续函数,且 v t( ) 0 ,计算在这段时间内物体所经过的路程 s . (2)解决过程: 在[ 1 2 T ,T ]内任意插入若干个分点 1 0 1 2 1 T2 T t t t t t = n− n = , 把[ 1 2 T ,T ]分成 n 个小段 [ 0 1 t ,t ],[ 1 2 t ,t ],., [ n n t ,t −1 ], 各小段时间的长依次为: 1 1 0 2 2 1 1 , , , n n n t t t t t t t t t = − = − = − − . 相应各段时间内物体经过的路程为:

△,△S2,.,△Sn 在[,]上任取一个时刻x,(≤T,≤1,),以x,时的速度(c)来代替[,]上各个 时刻的速度,则得:△心≈(c)山0=1,2,.,n) 进一步得到:3≈(c)△+)山,++Wr)△n=∑(c,)△ 设=mx4,A4,M}当元→0时,得:5=lm∑g,AM 二、定积分的定义 1.问题总结:由上述两例可见,虽然所计算的量不同,但它们都决定于一个函数及其 自变量的变化区间,其次它们的计算方法与步骤都相同,即归纳为一种和式极限,即 面积A=m∑f传)△x, 路程S=m∑T)△4,· 将这种方法加以概括,就可以抽象出下述定积分的定义。 2.定积分的定义设函数f(x)在[a,b)上有界,在[a,b]中任意插入若干个分点 a=X0<1<x2<.<xm-1<xn=b 把区间[a,b分成n个小区间 [x0,x][x,x2].,[xn-,xn] 各个小区间的长度依次为△x1=X-x0,△x2=x2-x,.,△xn=xn一X 在每个小区间[xx,]上任取一点5(≤≤x),作函数值f()与小区间长度A,的 乘积f(5)△x(=1,2,.,n),并作出和 S=∑fE)△x (1) 记元=max{△x,△x2,△xn,如果不论对[a,b怎样分法,也不论在小区间[x-1,x,]上点 怎样取法,只要当入→0时,和S总趋于确定的极限1,这时我们称这个极限I为函数
1 2 , , , n s s s . 在[ i i t ,t −1 ]上任取一个时刻 1 ( ) i i i i t t − ,以 i 时的速度 ( )i v 来代替[ i i t ,t −1 ]上各个 时刻的速度,则得: ( ) i i i s v t (i = 1,2, ,n) 进一步得到: 1 1 2 2 ( ) ( ) ( ) n n s v t v t v t + + + 1 ( ) n i i i v t = = . 设 = maxt 1 ,t 2 , ,t n ,当 → 0 时,得: 0 1 lim ( ) n i i i s v t → = = . 二、定积分的定义 1.问题总结:由上述两例可见,虽然所计算的量不同,但它们都决定于一个函数及其 自变量的变化区间,其次它们的计算方法与步骤都相同,即归纳为一种和式极限,即 面积 = → = n i i i A f x 1 0 lim ( ) , 路程 = → = n i i i S v T t 1 0 lim ( ) . 将这种方法加以概括,就可以抽象出下述定积分的定义. 2.定积分的定义 设函数 f x( ) 在 [ , ] a b 上有界,在 [ , ] a b 中任意插入若干个分点 a = x0 x1 x2 xn−1 xn = b 把区间 a,b 分成 n 个小区间 [ , ],[ , ], ,[ , ], 0 1 1 2 n 1 n x x x x x x − 各个小区间的长度依次为 1 1 0 2 2 1 1 , , , = − = − n = n − n− x x x x x x x x x . 在每个小区间[ i i x , x −1 ]上任取一点 1 ( i i i i x x − ),作函数值 ( )i f 与小区间长度 i x 的 乘积 ( ) ( 1,2, , ), i i f x i n = 并作出和 1 ( ) n i i i S f x = = . (1) 记 max{ , , , } 1 2 n = x x x ,如果不论对 a,b 怎样分法,也不论在小区间[ i i x , x −1 ]上点 i 怎样取法,只要当 →0 时,和 S 总趋于确定的极限 I ,这时我们称这个极限 I 为函数

fx)在区间[a,b上的定积分(简称积分),记作fx)dx,即 (dx=1m(Ax. (2) 其中fx)叫做被积函数,f(x)dx叫做被积表达式,x叫做积分变量,a叫做积分下限,b 叫做积分上限,[a,b叫做积分区间. 利用“6-6”的说法,上述定积分的定义可以表述如下: 设有常数1,如果对于任意给定的正数6总,存在一个正数δ,使得对于区间[4,b]的 任何分法,也不论三,在[x1,x,]中怎样取法,只要入<6,总有 I∑fG)Ax-1kE 成立,则称I是fx)在区间a,b上的定积分,记作∫fx)dx。 注意:1.当和∑f(5,)△x,的极限存在时,其极限I仅与被积函数f(x)及积分区间 [a,有关。 2,积分与积分变量的记法无关,即: ∫fx)dx=f)d1=∫f)du 3.S=立八G,A通常称为积分和.如果f)在区间血,)上的定积分存在,则说 fx)在[a,b上可积. 3.函数可积的两个充分条件 定理1设f(x)在a,b]上连续,则fx)在[a,b上可积. 定理2设f(x)a,b]上有界,且只有有限个间断点,则f(x)a,b]上可积. 4.定积分的几何意义 由前面的讨论知,当f(x)≥0时,函数f(x)在[a,b]的定积分」fx)dx在几何上表 示由曲线由直线x=a,x=b,y=0及曲线y=∫(x)所围成的曲边梯形的面积
f (x) 在区间 a,b 上的定积分(简称积分), 记作 ( )d b a f x x ,即 ( )d b a f x x = I = 0 1 lim ( ) n i i i f x → = , (2) 其中 f (x) 叫做被积函数, f x x ( )d 叫做被积表达式, x 叫做积分变量, a 叫做积分下限, b 叫做积分上限, a,b 叫做积分区间. 利用“ − ”的说法,上述定积分的定义可以表述如下: 设有常数 I ,如果对于任意给定的正数 总,存在一个正数 ,使得对于区间 a,b 的 任何分法,也不论 i 在[ i i x , x −1 ]中怎样取法,只要 ,总有 1 | ( ) | n i i i f x I = − 成立,则称 I 是 f (x) 在区间 a,b 上的定积分,记作 ( )d b a f x x . 注意:1.当和 1 ( ) n i i i f x = 的极限存在时,其极限 I 仅与被积函数 f (x) 及积分区间 a,b 有关. 2.积分与积分变量的记法无关,即: ( )d ( )d ( )d b b b a a a f x x f t t f u u = = . 3. 1 ( ) n i i i S f x = = 通常称为积分和.如果 f (x) 在区间 a,b 上的定积分存在,则说 f (x) 在 a,b 上可积. 3.函数可积的两个充分条件 定理 1 设 f (x)在[a,b] 上连续,则 f (x) 在 a,b 上可积. 定理 2 设 f (x)在[a,b] 上有界,且只有有限个间断点,则 f (x)在[a,b] 上可积. 4.定积分的几何意义 由前面的讨论知,当 f x( ) 0 时,函数 f (x)在[a,b] 的定积分 ( )d b a f x x 在几何上表 示由曲线由直线 x a = , x b = , y = 0 及曲线 y = f (x) 所围成的曲边梯形的面积.
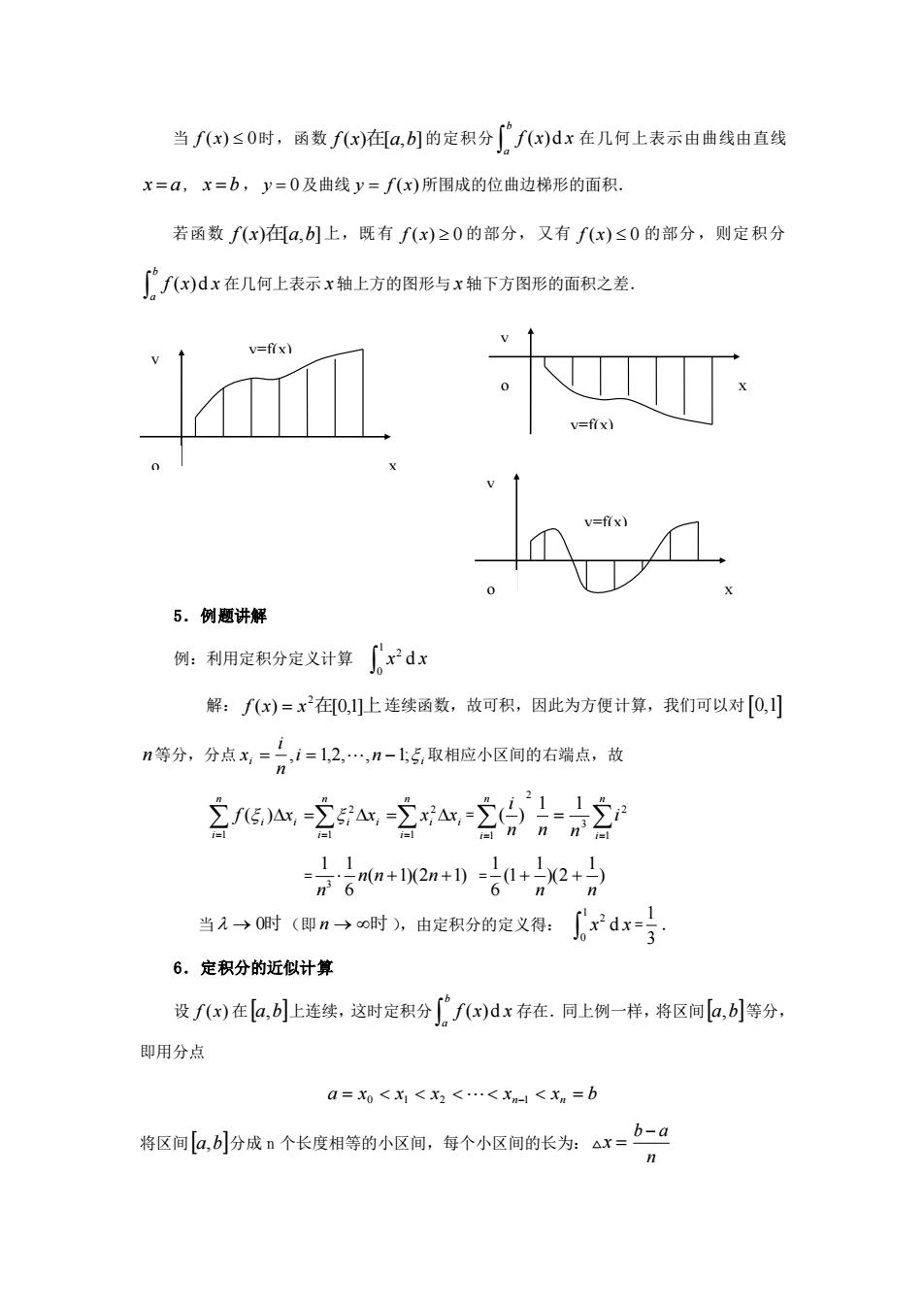
当fx)≤0时,函数fx)在a,的定积分[fx)dx在几何上表示由曲线由直线 x=a,x=b,y=0及曲线y=fx)所围成的位曲边梯形的面积 若函数f(x)a,b]上,既有f(x)≥0的部分,又有f(x)≤0的部分,则定积分 ∫f(x)dx在几何上表示x轴上方的图形与x轴下方图形的面积之差, v↑ v=fix =frx) v=f7x) 5.例题讲解 例:利用定积分定义计算[x2dx 解:fx)=x在0,止连续函数,故可积,因此为方便计算,我们可以对[0, n等分,分点x,=。i=12,.,1-上5,取相应小区间的右端点,故 5宫9- 名a+2m+)0+x2+的 当无→0时(即n→时),由定积分的定义得:rdx背 6.定积分的近似计算 设f(x)在[a,b上连续,这时定积分f(x)dx存在.同上例一样,将区间a,b等分, 即用分点 a=0<x<3<.<x<xn=b 将区间血,小分成n个长度相等的小区间,每个小区间的长为△x=-口
当 f x( ) 0 时,函数 f (x)在[a,b] 的定积分 ( )d b a f x x 在几何上表示由曲线由直线 x a = , x b = , y = 0 及曲线 y = f (x) 所围成的位曲边梯形的面积. 若函数 f (x)在[a,b] 上,既有 f x( ) 0 的部分,又有 f x( ) 0 的部分,则定积分 ( )d b a f x x 在几何上表示 x 轴上方的图形与 x 轴下方图形的面积之差. 5.例题讲解 例:利用定积分定义计算 1 2 0 x x d 解: f (x) = x 2在[0,1]上 连续函数,故可积,因此为方便计算,我们可以对 0,1 n 等分,分点 i n i i n i x = , = 1,2,, −1; 取相应小区间的右端点,故 = = = = = n i i i n i i i n i i i f x x x x 1 2 1 2 1 ( ) = = = = n i n i i n n n i 1 2 3 2 1 1 1 ( ) = 3 1 1 ( 1)(2 1) 6 n n n n + + = ) 1 )(2 1 (1 6 1 n n + + 当 → 0时 (即 n → 时 ),由定积分的定义得: 1 2 0 x x d = 3 1 . 6.定积分的近似计算 设 f (x) 在 a,b 上连续,这时定积分 ( )d b a f x x 存在.同上例一样,将区间 a,b 等分, 即用分点 a = x0 x1 x2 xn−1 xn = b 将区间 a,b 分成 n 个长度相等的小区间,每个小区间的长为: x = b a n − y=f(x) o x y o x y y=f(x) y=f(x) o x y

在小区间[x,x]上,取号=x应有 dx=-226)=恤22 从而,对任一确定的自然数n,有dx=2化) 记)=上式可写为dx2空 (3) 若取后=:则有近似公式dx气2空 (4) n 这种求定积分的近似值的方法称为矩形法.公式(3,、(4)称为矩形法公式。 三、定积分的性质 1.补充规定: (1)当ab时,fx)dx=0 (2)当ab时,∫f(x)dx=-∫f(x)dx(说明) 2.定积分的性质 性质1函数和(差)的定积分等于它们的定积分的和(差),即 [f(x)±gxdx=∫f(x)dx±∫g(xdx 证明:广/士g(x=m/5)±g5,A =典fGA出±典2gG4 =dx±gex)dx 性质2被积函数的常数因子可以提到积分号外面,即 ∫广(x)dx=k∫fx)dx(k是常数) 性质3如果将积分区间分成两部分,则在整个区间上的定积分等于这两个区间上定 积分之和,即设a<c<b,则 fx)dx=∫fx)dx+∫fx)dx
在小区间 1 [ , ] i i x x − 上,取 i = i 1 x − ,应有 ( )d b a f x x = 1 1 1 lim ( ) lim ( ) n n i i n n i i b a b a f f x n n − → → = = − − = , 从而,对任一确定的自然数 n ,有 ( )d b a f x x 1 1 ( ) n i i b a f x n − = − , 记 ( )i i f x y = ,上式可写为 ( )d b a f x x 1 0 ( ) n i i b a y n − = − , (3) 若取 i = i x ,则有近似公式 ( )d b a f x x 1 ( ) n i i b a y n = − . (4) 这种求定积分的近似值的方法称为矩形法.公式(3)、(4)称为矩形法公式. 三、定积分的性质 1.补充规定: (1)当 a=b 时, ( )d 0 b a f x x = (2)当 a>b 时, ( )d b a f x x = − ( )d b a f x x (说明) 2.定积分的性质 性质 1 函数和(差)的定积分等于它们的定积分的和(差),即 [ ( ) ( )]d b a f x g x x = ( )d b a f x x ( )d b a g x x 证明: [ ( ) ( )]d b a f x g x x = i n i i i f g x = → 1 0 lim [ ( ) ( )] = = → i n i i f x 1 0 lim ( ) i n i i g x = → 1 0 lim ( ) = ( )d b a f x x ( )d b a g x x 性质 2 被积函数的常数因子可以提到积分号外面,即 ( )d b a kf x x = k ( )d b a f x x ( k 是常数) 性质 3 如果将积分区间分成两部分,则在整个区间上的定积分等于这两个区间上定 积分之和,即设 a<c<b,则 ( )d b a f x x = ( )d c a f x x + ( )d b c f x x

注意:我们规定无论a,b,c的相对位置如何,总有上述等式成立. 性质4如果在区间[a,上,fx)=l,则心fx)dx=dx=b-a 性质5如果在区间[a,b]上,f(x)≥0,则 f(x)dx20 (ab,还是a<b, y↑ y=f八x) 上述等式恒成立。 f5) 积分中值定理的几何释意如下:在区间 [a,b]上至少存在一个5,使得以区间[a,b] 为底边,以曲线y=f(x)为曲边的曲边梯形 a b
注意:我们规定无论 abc , , 的相对位置如何,总有上述等式成立. 性质 4 如果在区间 [ , ] a b 上, f (x) 1,则 ( )d b a f x x = d b a x b a = − 性质 5 如果在区间 [ , ] a b 上, f (x) 0,则 ( )d 0 b a f x x (a b) 证明:因 f (x) 0, 故 f ( ) 0(i 1,2,3, ,n) i = ,又因 x 0(i 1,2, ,n) i = ,故 ( ) 0 1 = i n i i f x , 设 = max{x1 ,x2 , ,xn }, → o 时,便得欲证的不等式. 推论 1 如果在 [ , ] a b 上, f (x) g(x),则 ( )d b a f x x ( )d b a g x x (a b) 推论 2 ( )d b a f x x ( ) d b a f x x 性质 6 设 M 与 m 分别是函数 f (x)在[a,b] 上的最大值及最小值,则 m(b − a) ( )d b a f x x M (b − a) (a b) 性质 7 (定积分中值定理) 如果函数 f (x) 在闭区间 [ , ] a b 上连续,则在积分区间 [ , ] a b 上至少存在一点 ,使下式成立: ( )d ( )( ) b a f x x f b a = − ( a b ) 证明:利用性质 6, 1 ( )d b a m f x x M b a − ;再由闭区间上连续函数的介值定理, 知在 [ , ] a b 上至少存在一点 ,使 1 ( ) ( )d b a f f x x a b = − , 故得此性质.显然无论 a b ,还是 a b , 上述等式恒成立. 积分中值定理的几何释意如下:在区间 [a,b]上至少存在一个 ,使得以区间[a, b] 为底边, 以曲线 y = f (x) 为曲边的曲边梯形 y x o a b f ( ) y = f (x)

的面积等于同一底边而高为∫()的一个矩形的面积,见图. 技积分中值公式所得:化行产6厂达格为属数在区间上价平均值,如图所示 四、小结与思考: 1.重述定积分的定义,注意其中的两个“任意” 2.对连续变量的累积,一般采用分割,近似求和,取极限的方法进而归结到求定积分: 3.结合课后习题说明定积分性质的应用: 4.思考用怎样的思路可以求解曲顶柱体的体积 五、作业:作业卡 第二节微积分基本公式 教学目的:1.掌握变上限函数的意义和微积分基本公式: 2。能利用变上限函数的导数以及基本公式解决定积分的相关问题。 教学重点:微积分基本公式的应用 教学难点:变上限函数及微积分公式的应用. 教学过程: 一、变速直线运动中位置函数与速度函数之间的联系 1.问题分析:设一物体在一直线上运动,在这直线上取定原点,正方向,单位长度 使其成为一数轴,时刻t时物体所有的位置s(),速度)(不防设()≥0) 物体在时间间隔[口,T]内经过的路程可以用速度函数()在[T,T]上的定积分来表 达,即∫)dx. 另一方面,这段路程可以通过位置函数5()在区间[口,I]的增量来表示,即 S(T)-S(T) 故)d=ST)-ST) (1) 注意到S()=(),即s)是)的原函数.速度函数()在区间口,T]上的定积分 等于它的原函数路程函数s()在区间[T,T]上的增量S(T)-S(T)
的面积等于同一底边而高为 f ( ) 的一个矩形的面积, 见图. 按积分中值公式所得: 1 ( ) ( ) b a f f x dx a b = − 称为函数在区间上的平均值.如图所示. 四、小结与思考: 1.重述定积分的定义,注意其中的两个“任意”; 2.对连续变量的累积,一般采用分割,近似求和,取极限的方法进而归结到求定积分; 3.结合课后习题说明定积分性质的应用; 4.思考用怎样的思路可以求解曲顶柱体的体积. 五、作业:作业卡 第二节 微积分基本公式 教学目的:1.掌握变上限函数的意义和微积分基本公式; 2.能利用变上限函数的导数以及基本公式解决定积分的相关问题. 教学重点:微积分基本公式的应用. 教学难点:变上限函数及微积分公式的应用. 教学过程: 一、变速直线运动中位置函数与速度函数之间的联系 1.问题分析:设一物体在一直线上运动,在这直线上取定原点,正方向,单位长度, 使其成为一数轴,时刻 t 时物体所有的位置 s(t) ,速度 v(t)(不防设v(t) 0). 物体在时间间隔 [ , ] T1 T2 内经过的路程可以用速度函数 v(t) 在 [ , ] T1 T2 上的定积分来表 达,即 2 1 ( )d T T v t x . 另一方面,这段路程可以通过位置函数 s(t) 在区间 [ , ] T1 T2 的增量来表示,即 ( ) ( ) S T2 − S T1 故 2 1 ( ) T T v t dx = ( ) ( ) S T2 − S T1 (1) 注意到 S`(t) = v(t) ,即 s(t) 是 v(t) 的原函数.速度函数 v(t) 在区间 [ , ] T1 T2 上的定积分 等于它的原函数路程函数 s(t) 在区间 [ , ] T1 T2 上的增量 ( ) ( ) S T2 − S T1 .

2.结论推广假设:函数f(x)在区间[a,b]上连续,是否f(x)在区间[a,b]上的定积分 就等于的原函数(设为F(x)在区间[a,b)]上的增量:F(b)-F(a), 二、积分上限的函数及其导数 1.积分上限的函数:设f(x)在a,b)]上连续,并且设x为a,b]上任一点,有 (x)=∫f)dr (说明函数是如何得到的) 2.积分上限的函数性质: 定理1如果函数f(x)在区间[a,b]上连续,则积分上限函数 ()=∫f0d 在[a,b]上具有导数,并且它的导数是 o-话f0h=))(asx≤b) 证明:(1)x∈(a,b)时, △D(x)=D(x+△r)-(x) -[""fdr-ffdt -far+"rdi-frdr =f0)d 5在x与△r之间,应用积分中值定理,有D(x)=f(5)△x,所以 △①=f59 Ar→0时,有5→x,有mf(份)=f).故令△x→0,对上式两边取极限有: p'(x)=f(x) (2)x=a或b时考虑其单侧导数, 可得中(a=f(a),中(b)=f(b) 由定理1可得下面结论:
2.结论推广假设:函数 f (x) 在区间 [a,b] 上连续,是否 f (x) 在区间 [a,b] 上的定积分 就等于的原函数(设为 F x( ) )在区间 [a,b] 上的增量: F b F a ( ) ( ) − . 二、积分上限的函数及其导数 1.积分上限的函数:设 f (x) 在 [a,b] 上连续,并且设 x 为 [a,b] 上任一点,有 ( ) ( )d x a = x f t t (说明函数是如何得到的) 2.积分上限的函数性质: 定理 1 如果函数 f (x) 在区间 [a,b] 上连续,则积分上限函数 = x a (x) f (t)dt 在 [a,b] 上具有导数,并且它的导数是 = x a f t dt dx d (x) ( ) = f (x) ( a x b ) 证明:(1) x (a,b) 时, (x) = (x + x) − (x) = ( )d x x a f t t + − ( )d x a f t t = ( )d ( )d ( )d x x x x a x a f t t f t t f t t + + − = ( )d x x x f t t + 在 x与x 之间,应用积分中值定理,有 (x) = f x ( ) ,所以 ( ) ( ) f x x = x →0 时,有 → x ,有 0 lim ( ) ( ) x f f x → = .故令 x →0 ,对上式两边取极限有: (x) = f (x) (2) x = a或b时考虑 其单侧导数, 可得 ( ) a + = f (a) , ( ) b − = f (b). 由定理 1 可得下面结论:

定理2如果函数f(x)在区间[a,b]上连续,则函数 (x)=[f(r)dr 是f(x)的一个原函数. 意义:1.肯定了连续函数的原函数是存在的:2.初步揭示了积分学中定积分与原函数之 间的关系 三、Newton-Leibniz公式 1.定理3如果函数F(x)是连续函数f(x)在区间[a,b]上的一个原函数,则 ["f(x)dx=F(b)-F(a) (4) 证明:因F(x)与p(x)均是f(x)原函数,故 F(x)-(x)=C(a≤x≤b) 又因F(a)-p(a)=C且p(a)=0,故C=F(a):于是fx)dx=F()-F(a,当 x=b时,即有[fx)dx=F(b)-F(a). 将F(b)-F(a)记作[F(x)],即[f(x)=[F(x)]. 上述公式就是Newton一Leibniz公式,也称作微积分基本公式,定积分与被积函数的 原函数或不定积分之间的关系-一一个连续函数(x)在区间[a,b]上的定积分等于它的任 一个原函数在区间[α,b]上的增量.公式(4)提供了定积分的计算方法。 2.例题讲解 a5号 例2# 解doe- 例3g 解:dx=[n=lni-h2=-h2. 例4计算y=smnx在[0,π]上与x轴所围成平面图形的面积
定理 2 如果函数 f (x) 在区间 [a,b] 上连续,则函数 (x) = x a f (t)dt 是 f (x) 的一个原函数. 意义:1.肯定了连续函数的原函数是存在的;2.初步揭示了积分学中定积分与原函数之 间的关系. 三、Newton —Leibniz 公式 1.定理 3 如果函数 F(x) 是连续函数 f (x) 在区间 [a,b] 上的一个原函数,则 ( )d b a f x x = F(b) − F(a) (4) 证明:因 F(x) 与 (x) 均是 f (x) 原函数,故 F(x) − ( ) x =C ( a x b ) 又因 F a a C ( ) ( ) − = 且 = ( ) 0 a ,故 C F a = ( ) ;于是 ( )d ( ) ( ) b a f x x F x F a = − ,当 x b = 时,即有 ( )d b a f x x = F(b) − F(a) . 将 F(b) − F(a) 记作[ F(x) ] b a ,即 = b a f (x)dx [ F(x) ] b a . 上述公式就是 Newton —Leibniz 公式,也称作微积分基本公式,定积分与被积函数的 原函数或不定积分之间的关系-一个连续函数 f (x) 在区间 [a,b] 上的定积分等于它的任 一个原函数在区间 [a,b] 上的增量.公式(4)提供了定积分的计算方法. 2.例题讲解 例 1 1 3 3 3 1 2 0 0 1 0 1 d 3 3 3 3 x x x = = − = . 例 2 计算 3 2 1 1 d 1 x x − + . 解: 3 2 1 1 d 1 x x − + = 12 3 7 arctgx −1 = . 例 3 1 2 d x x − − . 解: 1 1 2 2 1 d ln ln1 ln 2 ln 2 x x x − − − − = = − = − . 例 4 计算 y = sin x 在[ 0, ]上与 x 轴所围成平面图形的面积.