
第一章函数与极限 一、学时分配: 讲课学时:16学时 习题课学时:2学时共18学时 二、基本内容: 映射与函数,复合函数、分段函数、隐函数与反函数的概念,函数的单调性、有界性 奇偶性、周期性:基本初等函数、初等函数:数列极限、函数极限的概念,极限的四则运算 无穷小与无穷大,无穷小的阶的比较,函数的连续性概念,间断点及其分类,连续函数的基 本性质,初等函数的连续性。 三、教学要求: 1.理解映射与函数的概念,掌握函数的表示方法,并会建立简单应用问题中的函数关系 式。 2.了解函数的奇偶性、单调性、周期性和有界性。 3.理解复合函数及分段函数的概念,了解反函数及隐函数的概念。 4.掌握基木初等函数的性质及其图形。 5.理解极限的概念,理解函数左极限与右极限的概念,以及极限存在与左、右极限之间的 关系。 6.掌握极限的性质及四则运算法则。 7.了解极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极限的方法。 8.理解无穷小、无穷大的概念,掌握无穷小的比较方法,会用等价无穷小求极限 9.理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型。 10.了解连续函数的性质和初等函数的连续性,了解闭区间上连续函数的性质(有界性、 最大值和最小值定理、介值定理),并会应用这些性质。 四、重点难点 1,重点函数与复合函数的概念,基本初等函数与初等承数,实际间题中的函数关系 极限概念与极限运算, 无穷小 两个重要极限公式,函数连续的概念与初等函数的连续性, 2.难点函数符号的运用,复合函数的复合过程,极限定义的理解,两个重要极限的 灵活运用
第一章 函数与极限 一、学时分配: 讲课学时:16 学时 习题课学时:2 学时 共 18 学时 二、基本内容: 映射与函数,复合函数、分段函数、隐函数与反函数的概念,函数的单调性、有界性、 奇偶性、周期性;基本初等函数、初等函数;数列极限、函数极限的概念,极限的四则运算, 无穷小与无穷大,无穷小的阶的比较,函数的连续性概念,间断点及其分类,连续函数的基 本性质,初等函数的连续性。 三、教学要求: 1.理解映射与函数的概念,掌握函数的表示方法,并会建立简单应用问题中的函数关系 式。 2.了解函数的奇偶性、单调性、周期性和有界性。 3.理解复合函数及分段函数的概念,了解反函数及隐函数的概念。 4.掌握基本初等函数的性质及其图形。 5.理解极限的概念,理解函数左极限与右极限的概念,以及极限存在与左、右极限之间的 关系。 6.掌握极限的性质及四则运算法则。 7.了解极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极限的方法。 8.理解无穷小、无穷大的概念,掌握无穷小的比较方法,会用等价无穷小求极限。 9.理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型。 10.了解连续函数的性质和初等函数的连续性,了解闭区间上连续函数的性质(有界性、 最大值和最小值定理、介值定理),并会应用这些性质。 四、重点难点 1.重点 函数与复合函数的概念,基本初等函数与初等函数,实际问题中的函数关系, 极限概念与极限运算,无穷小,两个重要极限公式,函数连续的概念与初等函数的连续性。 2.难点 函数符号的运用,复合函数的复合过程,极限定义的理解,两个重要极限的 灵活运用

第一节映射与函数 教学目的:理解映射与函数的概念,掌握函数的各种性态,并会建立简单应用问 题中的函数关系式。 教学重点:函数的概念,函数的各种性态 教学难点:反函数、复合函数、分段函数的理解 教学过程: 一、集合 1.集合概念 定义1.具有某种特定性质的事物的总体称为集合。 集合可用大写的字母ABGD等标识 组成集合的事物称为该集合的元素。 集合的元素可用小写的字母品么G,d等标识。 不含任何元素的集合称为空集,记作② a是集合A的元素记为aeA读作a属于A a不是集合A的元素记为aA,读作a不属于A 如果集合A的元素都是集合B的元素,则称A是B的子集,记为kB(读作A包含于, 集合的表示: (1)列举法:把集合的全体元素一一列举出来 例如仁{1,2,3,4,5,6,7. (2)描述法:若集合M是由具有某种性质P的元素x的全体所组成,则M可表示为 {x|x具有性质P. 例如A{x2-1=0. 自然数集N=(xx是自然数} 实数集R={xx是实数 整数集Z={xx是整数) 有理集Q{xx是有理数} 定义2.如果集合A的元素都是集合B的元素,则称A是B的子集,记为仁B(读作A包含 于 若kB且民A,则称A与B相等,记作卡R
第一节 映射与函数 教学目的:理解映射与函数的概念,掌握函数的各种性态,并会建立简单应用问 题中的函数关系式。 教学重点:函数的概念,函数的各种性态 教学难点:反函数、复合函数、分段函数的理解 教学过程: 一、集合 1.集合概念 定义 1. 具有某种特定性质的事物的总体称为集合. 集合可用大写的字母 A, B, C, D 等标识. 组成集合的事物称为该集合的元素. 集合的元素可用小写的字母 a, b, c, d 等标识. 不含任何元素的集合称为空集 ,记作 . a 是集合 A 的元素记为 aA, 读作 a 属于 A. a 不是集合 A 的元素记为 aA, 读作 a 不属于 A. 如果集合 A 的元素都是集合 B 的元素, 则称 A 是 B 的子集, 记为 AB(读作 A 包含于 B). 集合的表示: (1)列举法:把集合的全体元素一一列举出来. 例如 A={1, 2,3, 4, 5, 6, 7}. (2)描述法:若集合 M 是由具有某种性质 P 的元素 x 的全体所组成, 则 M 可表示为 M={x | x 具有性质 P }. 例如 B={x| x2-1=0}. 自然数集 N={x| x 是自然数} 实数集 R={x| x 是实数} 整数集 Z={x| x 是整数} 有理集 Q={x| x 是有理数} 定义 2. 如果集合 A 的元素都是集合 B 的元素, 则称 A 是 B 的子集, 记为 AB(读作 A 包含 于 B). 若 AB 且 BA,则称 A 与 B 相等,记作 A=B

2.集合的运算 设A、B是两个集合,则 AU{xxEA或xE称为A与B的并集(简称并) An:{xxEA且xe称为A与B的交集(简称交). 八A{xxeA且xg品称为A与B的差集(简称差). AC八上{xxg》为称A的余集或补集,其中I为全集 在两个集合之间还可以定义直积(笛卡儿乘积) 设A、B是任意两个集合,则有序对集合 x(xxeA且E 称为集合A与集合B的直积 例如,RxR={(x,川ER且ER)即为xO面上全体点的集合,RxR常记作R2. 集合运算的法则: 设A、RC为任意三个集合,则有 (1)交换律AU:BUA A0BB n 4: (②)结合律(AU)UAU(BUO, (A U Bn Cn(B n (3)分配律(AUnC(4n0U(BnO, (MUBUG(AUO∩(BUO (④对偶律(U B CAC n BC.(An B)G=ACU BC 3.区间和邻域 数集{xaK称为开区间, 记为(a,),即(a,)=(xKK 闭区间[a,={x函s卧 半开区间[a,)=(xa飞K, (a,]=xlaxsb) 上述区间都是有限区间,其中a和b称为区间的端点,数a称为区间的长度 此外还有所谓无限区间: [a,+o)={xa匹小, (-m,={xx飞
2. 集合的运算 设 A、B 是两个集合, 则 A∪B={x|xA 或 xB}称为 A 与 B 的并集(简称并). A∩B={x|xA 且 xB}称为 A 与 B 的交集(简称交). A\B={x|xA 且 xB}称为 A 与 B 的差集(简称差). AC=I\A={x|xA}为称 A 的余集或补集, 其中 I 为全集. 在两个集合之间还可以定义直积(笛卡儿乘积) 设 A、B 是任意两个集合, 则有序对集合 AB={(x, y)|xA 且 yB} 称为集合 A 与集合 B 的直积. 例如, RR={(x, y)| xR 且 yR }即为 xOy 面上全体点的集合, RR 常记作 R2. 集合运算的法则: 设 A、B、C 为任意三个集合, 则有 (1)交换律 A∪B=B ∪ A, A∩B=B ∩ A; (2)结合律 (A ∪ B) ∪ C=A ∪(B ∪ C), (A ∪ B) ∩ C=A ∩(B ∩ C); (3)分配律 (A ∪ B) ∩ C=(A ∩ C) ∪(B ∩ C), (A ∪ B) ∪ C=(A ∪ C) ∩(B ∪ C); (4)对偶律 (A ∪ B)C=AC ∩ BC, (A∩B)C=AC∪BC. 3.区间和邻域 数集{x|a<x<b}称为开区间, 记为(a, b), 即 (a, b)={x|a<x<b}. 闭区间 [a, b]={x|axb} 半开区间[a, b)={x|ax<b}, (a, b]={x|a<xb}. 上述区间都是有限区间, 其中 a 和 b 称为区间的端点, 数 b-a 称为区间的长度. 此外还有所谓无限区间: [a, +)={ x|ax}, (-, b]={ x|xb}

(a,+∞)={xK, (-o,)={xK (-o,+o)=实数集R 以点a为中心的任何开区间称为点a的邻域,记作(). 设0,则称八a,=(xa6《Ka+d={xxaKd为点a的6邻域,其中点a称 为邻域的中心,6称为邻域的半径 点a的去心6邻域 八a,={x0<|xral<. 二、映射 1.映射概念 定义4.设术Y是两个非空集合,如果存在一个法则(使得对中每个元素x,按法则£在 Y中有唯一确定的元素y与之对应,则称f为从X到Y的映射,记作 f:K→K y称为元素x(在映射上下的像,并记作,即=,元素x称为元素(在映射下 的一个原像: 集合X称为映射f的定义域,记作D,即DeX X中所有元素的像所组成的集合称为映射f的值域, 记为f,或fD,即E=f)={f)lxe. 注意: )映射的三要素一定义域,对应规则,值域, 2)对每个x∈X元素x的像y是唯一的:但对每个yER元素y的原像不一定唯一 例1设f:R→R,对每个xeRf)=2.f是一个映射,f的定义域Df=R, 值域Rf={20以. 例2设上{(x,l2+2=I,上{(x0)1川xs1,f:g对每个(x功ex 有唯一确定的(x,0)eP与之对应.f是一个映射,f的定义域DEX值域F=E 在几何上,这个映射表示将平面上一个圆心在原点的单位圆周上的点投影到x轴的区间[-1, 1上. 满射、单射和双射: 设f是从集合X到集合Y的映射. 若F=上即P中任一元素y都是X中某元素的像,则称f为X 到Y上的映射或满射:
(a, +)={ x|a0, 则称 U(a, )={x| a- < x< a+}={x| |x-a|<}为点 a 的 邻域,其中点 a 称 为邻域的中心, 称为邻域的半径. 点 a 的去心 邻域 U(a, )={x|0<|x-a|<}. 二、映射 1. 映射概念 定义4.设X、Y是两个非空集合, 如果存在一个法则f, 使得对X中每个元素x, 按法则f, 在 Y 中有唯一确定的元素 y 与之对应, 则称 f 为从 X 到 Y 的映射, 记作 f : X→Y. y 称为元素 x(在映射 f 下)的像, 并记作 f(x), 即 y=f(x),元素 x 称为元素 y(在映射 f 下) 的一个原像; 集合 X 称为映射 f 的定义域, 记作 Df , 即 Df=X. X 中所有元素的像所组成的集合称为映射 f 的值域, 记为 Rf , 或 f(X), 即 Rf =f(X)={f(x)|xX}. 注意: 1)映射的三要素— 定义域 , 对应规则 , 值域 . 2)对每个 xX,元素 x 的像 y 是唯一的; 但对每个 yR 元素 y 的原像不一定唯一 . 例 1 设 f : R→R, 对每个 xR, f(x)=x2.f 是一个映射, f 的定义域 Df =R, 值域 Rf ={y|y0}. 例 2 设 X={(x, y)|x2+y2=1},Y={(x, 0)||x|1},f : X→Y,对每个(x, y)X, 有唯一确定的(x, 0)Y 与之对应.f 是一个映射, f 的定义域 Df=X, 值域 Rf =Y. 在几何上,这个映射表示将平面上一个圆心在原点的单位圆周上的点投影到 x 轴的区间[−1, 1]上. 满射、单射和双射: 设 f 是从集合 X 到集合 Y 的映射. 若 Rf =Y, 即 Y 中任一元素 y 都是 X 中某元素的像, 则称 f 为 X 到 Y 上的映射或满射;

若对X中任意两个不同元素1≠2,它们的像f代x1)≠(2),则称f为X到P的单射: 若映射f既是单射,又是满射,则称f为一一映射(域双射). 从实数集(或其子集)X到实数集Y的映射通常称为定义在X上的函数 2。逆映射与复合映射 设f是到的单射,则由定义,对每个EF,有唯一的x,适合()=5于是,我 们可定义一个从到X的新映射即 g:Rf→X, 对每个yeF,规定g()=x,这x满足(x)=g这个映射g称为f的逆映射,记作f-l, 其定义域为M,值域为X. 例如,映射y=x2,x∈(-0,0],其逆映射为y=-√x,x∈[0,+o) 按定义,只有单射才存在逆映射。 设有两个映射g:,f:2→乙其中1c2.则由映射g和f可以定出一个从X到2 的对 立法到 它将每 映射成 这个对应法则确定了 一个从X到 的映射,这个映射称为映射g和f构成的复合映射,记作f0品 多 fogK→Z (fo(=fg()],xEr. 说明 映射g和F构成复合映射的条件是:g的值域R必须包含在f的定义域内,即RcDf, 映射的复合是有顺序的,f0g有意义并不表示g0f也有意义.即使它们都有意义,f0g 与g0f也未必相同: 例3设有映射g:R→[-1,1],对每个xeR,g()=sinx映射f:[-1,1]→[0,],对 每个u∈-L,f(0=V1-2,则映射g和f构成复映射f0g:R→[0,1],对每个xR, 交 (fogx)=f几g(x】=f(sinx)=V1-sin2x=cosx 三、函数 1.函数的定义:设x和y是两个变量,D是一个给定的数集,如果对于给定的每个数 x∈D,变量y按照一定法则总有确定的数值和它对应,则称y是x的函数,记作 y=f(x),数集D叫做这个函数的定义域,x叫做自变量,y叫做因变量,y的取值
若对 X 中任意两个不同元素 x1x2, 它们的像 f(x1)f(x2), 则称 f 为 X 到 Y 的单射; 若映射 f 既是单射, 又是满射, 则称 f 为一一映射(或双射). 从实数集(或其子集)X 到实数集 Y 的映射通常称为定义在 X 上的函数. 2. 逆映射与复合映射 设 f 是 X 到 Y 的单射, 则由定义, 对每个 yRf , 有唯一的 xX, 适合 f(x)=y, 于是, 我 们可定义一个从 Rf 到 X 的新映射 g, 即 g : R f →X, 对每个 yRf , 规定 g(y)=x, 这 x 满足 f(x)=y. 这个映射 g 称为 f 的逆映射, 记作 f −1, 其定义域为 Rf , 值域为 X . 例如, 映射 2 y x x = − , ( , 0] , 其逆映射为 y x = − , x + [ 0, ) 按定义,只有单射才存在逆映射。 设有两个映射 g : X→Y1, f : Y2→Z, 其中 Y1Y2. 则由映射 g 和 f 可以定出一个从 X 到 Z 的对应法则, 它将每个 xX 映射成 f[g(x)]Z. 显然, 这个对应法则确定了一个从 X 到 Z 的映射, 这个映射称为映射 g 和 f 构成的复合映射, 记作 f o g, 即 f o g: X→Z, (f o g)(x)=f[g(x)], xX . 说明: 映射 g 和 f 构成复合映射的条件是: g 的值域 R 必须包含在 f 的定义域内,即 R D f . 映射的复合是有顺序的,f o g 有意义并不表示 g o f 也有意义. 即使它们都有意义,f o g 与 g o f 也未必相同. 例 3 设有映射 g : R→[−1, 1], 对每个 xR, g(x)=sin x, 映射 f :[ 1,1] [0,1] − → ,对 每个 2 u f u u − = − [ 1,1], ( ) 1 .则映射 g 和 f 构成复映射 f o g: R→[0, 1],对每个 xR, 有 2 ( )( ) [ ( )] (sin ) 1 sin cos f g x f g x f x x x = = = − = . 三、函数 1. 函数的定义:设 x 和 y 是两个变量, D 是一个给定的数集,如果对于给定的每个数 xD ,变量 y 按照一定法则总有确定的数值和它对应,则称 y 是 x 的函数,记作 y = f (x) ,数集 D 叫做这个函数的定义域, x 叫做自变量, y 叫做因变量. y 的取值

范围叫函数的值域, 2.定义域的求法原则 (1)分母不为零 (2)√,x≥0 (3)lnx,x>0 (4)arcsinx,arccos x,-l≤x≤1 (5)同时含有上述四项时,要求使各部分都成立的交集 3.分段函数 用两个以上表达式表达的函数关系叫分段函数 如)=+kx≥1 x-I,x<I x=1称为分段点 4.复合函数 若y=f回u=(x),当(x)的值域落在f)的定义域内时 称y=f(x】是由中间变量u复合成的复合函数, 5.反函数 设函数的定义域为D,值域为V,·对于任意的y∈V,在D,上至少可以确定一个x 与y对应,且满足y=fx).如果把y看作自变量,x看作因变量,就可以得到一个新的 函数:x=∫(y).我们称这个新的函数x=f-(y)为函数y=fx)的反函数,而把函数 y=fx)称为直接函数。 应当说明的是,虽然直接函数y=fx)是单值函数,但是其反函数x=∫y)却不一 定是单值的.例如,y=fx)=x2的定义域为D,=R,值域',=[0,+o).任取非零的 y∈',则适合y=x之的x的数值有两个:x=√少x=-下.所以,直接函数y=x2 的反函数x=f-y)是多值函数:x=±√y.如果把x限制在区间0,+∞)上,则直接函 数y=x2,x∈0,+∞)的反函数x=V少是单值的.并称x=√少为直接函数y=x2, x∈R的反函数的一个单值分支.显然,反函数的另一个单值分支为x=-√少 个函数若有反函数,则有恒等式f[fx】■x,x∈D
范围叫函数的值域. 2. 定义域的求法原则 (1)分母不为零 (2) x,x 0 (3) ln , 0 x x (4) arcsin , arccos , 1 1 x x x − (5)同时含有上述四项时,要求使各部分都成立的交集 3. 分段函数 用两个以上表达式表达的函数关系叫分段函数 如 ( ) − + = 1 1 1 1 x x x x f x , , x =1 称为分段点 4. 复合函数 若 y = f (u) u =(x) ,当 (x) 的值域落在 f (u) 的定义域内时 称 y = f(x) 是由中间变量 u 复合成的复合函数. 5. 反函数 设函数的定义域为 D f ,值域为 Vf .对于任意的 Vf y ,在 D f 上至少可以确定一个 x 与 y 对应,且满足 y = f (x) .如果把 y 看作自变量, x 看作因变量,就可以得到一个新的 函数: x f (y) −1 = .我们称这个新的函数 x f (y) −1 = 为函数 y = f (x) 的反函数,而把函数 y = f (x) 称为直接函数. 应当说明的是,虽然直接函数 y = f (x) 是单值函数,但是其反函数 x f (y) −1 = 却不一 定是单值的.例如, ( ) 2 y = f x = x 的定义域为 Df = R ,值域 = 0,+ ) Vf .任取非零的 Vf y ,则适合 2 y = x 的 x 的数值有两个: x = y x = − y 1 , 2 .所以,直接函数 2 y = x 的反函数 x f (y) −1 = 是多值函数: x = y .如果把 x 限制在区间 0,+ ) 上,则直接函 数 2 y = x , x0,+ ) 的反函数 x = y 是单值的.并称 x = y 为直接函数 2 y = x , xR 的反函数的一个单值分支.显然,反函数的另一个单值分支为 x = − y . 一个函数若有反函数,则有恒等式 ( ) Df f f x x x −1 , .

相应地有-y)=y,yeV 例如,直接函数y=f)=子x+3x∈R的反函数为x=一6)=北-3引yeR #有e-2+小-,o-y 由于习惯上x表示自变量,y表示因变量,于是我们约定y=(似)也是直接函数 y=fx)的反函数. 反函数x=~y)与y=∫(),这两种形式都要用到.应当说明的是函数y=x)与 它的反函数x=∫y)具有相同的图形.而直接函数y=fx)与反函数y=∫()的图形 是关于直线y=x对称的. 6.函数的性质 (1)有界性 若有正数M存在,使函数∫)在区间1上恒有/x≤M,则称(x)在区间I上是 有界函数:否则,fx)在区间1上是无界函数. 如果存在常数M(不一定局限于正数),使函数f(x)在区间I上恒有fx)≤M,则称 f(x)在区间I上有上界,并且任意一个N≥M的数N都是f(x)在区间I上的一个上界: 如果存在常数m,使f(x)在区间I上恒有f(x)≥m,则称fx)在区间I上有下界,并且 任意一个I≤m的数1都是f(x)在区间1上的一个下界。 显然,函数fx)在区间I上有界的充分必要条件是f(x)在区间I上既有上界又有下界。 (2)单调性 设函数)在区间1上的任意两点x,)。 则称y=fx)在区间1上为严格单调增加(或严格单调减少)的函数. 如果函数fx)在区间1上的任意两点x<x2,都有f:)sfx)(或 x)之fx,),则称y=fx)在区间1上为广义单调增加(或广义单调减少)的函数.广 义单调增加的函数,通常简称为单调增加的函数或非减函数:广义单调减少的函数则简称为 单调减少的函数或非增函数. 例如,函数y=x2在区间(仁0,0)内是严格单调减少的:在区间(0,+∞)内是严格单调
相应地有 ( ) Vf f f y y y −1 , . 例如,直接函数 y = f (x) = x + 3,x R 4 3 的反函数为 x = f (y) = (y − ) y R − 3, 3 1 4 , 并且有 f f (x) x x − = + − 3 3 4 3 3 1 4 , f f (y) (y ) + y = − − 3 3 3 4 4 1 3 . 由于习惯上 x 表示自变量, y 表示因变量,于是我们约定 y f (x) −1 = 也是直接函数 y = f (x) 的反函数. 反函数 x f (y) −1 = 与 y f (x) −1 = ,这两种形式都要用到.应当说明的是函数 y = f (x) 与 它的反函数 x f (y) −1 = 具有相同的图形.而直接函数 y = f (x) 与反函数 y f (x) −1 = 的图形 是关于直线 y = x 对称的. 6. 函数的性质 (1)有界性 若有正数 M 存在,使函数 f (x) 在区间 I 上恒有 f (x) M ,则称 f (x) 在区间 I 上是 有界函数;否则, f (x) 在区间 I 上是无界函数. 如果存在常数 M (不一定局限于正数),使函数 f (x) 在区间 I 上恒有 f(x) M,则称 f (x) 在区间 I 上有上界,并且任意一个 N M 的数 N 都是 f (x) 在区间 I 上的一个上界; 如果存在常数 m ,使 f (x) 在区间 I 上恒有 f (x) m ,则称 f (x) 在区间 I 上有下界,并且 任意一个 l m 的数 l 都是 f (x) 在区间 I 上的一个下界. 显然,函数 f (x) 在区间 I 上有界的充分必要条件是 f (x) 在区间 I 上既有上界又有下界. (2)单调性 设函数 f (x) 在区间 I 上的任意两点 1 2 x x ,都有 ( ) ( ) 1 2 f x f x (或 ( ) ( ) 1 2 f x f x ), 则称 y = f (x) 在区间 I 上为严格单调增加(或严格单调减少)的函数. 如果函数 f (x) 在区间 I 上的任意两点 1 2 x x ,都有 ( ) ( ) 1 2 f x f x ( 或 ( ) ( ) 1 2 f x f x ),则称 y = f (x) 在区间 I 上为广义单调增加(或广义单调减少)的函数.广 义单调增加的函数,通常简称为单调增加的函数或非减函数;广义单调减少的函数则简称为 单调减少的函数或非增函数. 例如,函数 2 y = x 在区间 (− ,0) 内是严格单调减少的;在区间 (0,+ ) 内是严格单调

增加的. 而函数y=x、y=x在区间(0,+∞)内都是严格单调增加的 (3)奇偶性 若函数fx)在关于原点对称的区间I上满足f(x)=x)(或(x)=-∫(x))则称 fx)为偶函数(或奇函数). 偶函数的图形是关于y轴对称的:奇函数的图形是关于原点对称的。 例如,()=x己、g(d=xsmx在定义区间上都是偶函数.而F(d)=x、 Gx)=xcOSx在定义区间上都是奇函数. (4)周期性 对于函数y=x),如果存在一个非零常数T,对一切的x均有(x+T)=f(x),则称 函数f(x)为周期函数。并把T称为f(x)的周期.应当指出的是,通常讲的周期函数的周期 是指最小的正周期。 对三角函数而言,y=snx、y=cosx都是以2π为周期的周期函数,而y=anx、 y=cotx则是以π为周期的周期函数. 关于函数的性质,除了有界性与无界性之外,单调性、奇偶性、周期性都是函数的特殊 性质,而不是每一个函数都一定具备的。 7.初等函数 幂函数、指数函数、对数函数、三角函数、反三角函数和常数这6类函数叫做基本初等 函数.这些函数在中学的数学课程里己经学过, (1)幂函数y=x(ae风) 它的定义域和值域依a的取值不同而不同,但是 无论a取何值,幂函数在x∈(0,+0)内总有定义.当 1 a∈N或a=2nneN时,定义域为R.常见 的幂函数的图形如图11所示 (2)指数函数y=a'(a>0,a≠) 它的定义域为(0,+0),值域为(0,+∞).指数函数的 图形如图1-2所示
增加的. 而函数 3 y = x、y = x 在区间 (−,+ ) 内都是严格单调增加的. (3)奇偶性 若函数 f (x) 在关于原点对称的区间 I 上满足 f (− x) = f (x) (或 f (− x) = − f (x) )则称 f (x) 为偶函数(或奇函数). 偶函数的图形是关于 y 轴对称的;奇函数的图形是关于原点对称的. 例如, f (x) x g(x) xsin x 2 = 、 = 在定义区间上都是偶函数.而 F(x) = x 、 G(x) = xcos x 在定义区间上都是奇函数. (4)周期性 对于函数 y = f (x) ,如果存在一个非零常数 T ,对一切的 x 均有 f (x +T) = f (x) ,则称 函数 f (x) 为周期函数.并把 T 称为 f (x) 的周期.应当指出的是,通常讲的周期函数的周期 是指最小的正周期. 对三角函数而言, y = sin x、y = cos x 都是以 2 为周期的周期函数,而 y = tan x 、 y = cot x 则是以 为周期的周期函数. 关于函数的性质,除了有界性与无界性之外,单调性、奇偶性、周期性都是函数的特殊 性质,而不是每一个函数都一定具备的. 7. 初等函数 幂函数、指数函数、对数函数、三角函数、反三角函数和常数这 6 类函数叫做基本初等 函数.这些函数在中学的数学课程里已经学过. (1)幂函数 y x (a R) a = 它的定义域和值域依 a 的取值不同而不同,但是 无论 a 取何值,幂函数在 x(0,+) 内总有定义.当 a N 或 n N n a − = , 2 1 1 时,定义域为 R .常见 的幂函数的图形如图 1-1 所示. (2)指数函数 y = a (a 0 a 1) x , 它的定义域为 (−,+ ) ,值域为 (0,+ ) .指数函数的 图形如图 1-2 所示. 图 1-1 图 1-2
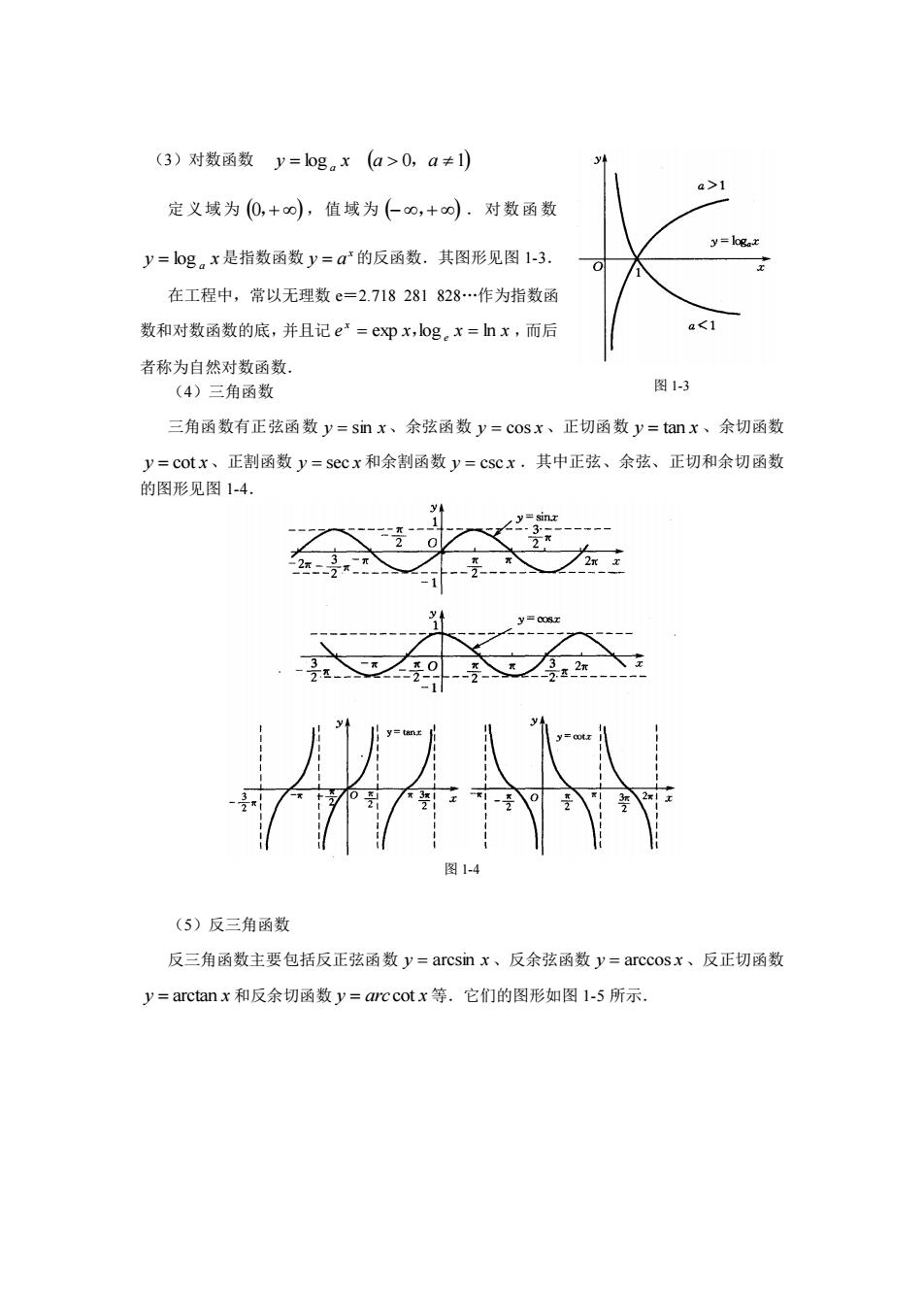
(3)对数函数y=log。x(a>0,a≠) 定义域为(0,+o),值域为(o,+∞).对数函数 y=log。x是指数函数y=口的反函数.其图形见图1-3. 在工程中,常以无理数e=2.718281828.作为指数函 数和对数函数的底,并且记e=epx,log。x=nx,而后 4<1 者称为自然对数函数, (4)三角函数 图1-3 三角函数有正弦函数y=sinx、余弦函数y=cosx、正切函数y=tanr、余切函数 y=cotx、正割函数y=sCcx和余割函数y=csCx.其中正弦、余弦、正切和余切函数 的图形见图14. (5)反三角函数 反三角函数主要包括反正弦函数y=arcsin x、反余弦函数y=arccosx、反正切函数 y=arctanx和反余切函数y=arccotx等.它们的图形如图l-5所示
(3)对数函数 y = log x (a 0 a 1) a , 定义域为 (0,+ ) ,值域为 (−,+ ) .对数函数 y x a = log 是指数函数 x y = a 的反函数.其图形见图 1-3. 在工程中,常以无理数 e=2.718 281 828.作为指数函 数和对数函数的底,并且记 e x x x e x = exp ,log = ln ,而后 者称为自然对数函数. (4)三角函数 三角函数有正弦函数 y = sin x 、余弦函数 y = cos x 、正切函数 y = tan x 、余切函数 y = cot x 、正割函数 y = sec x 和余割函数 y = csc x .其中正弦、余弦、正切和余切函数 的图形见图 1-4. (5)反三角函数 反三角函数主要包括反正弦函数 y = arcsin x 、反余弦函数 y = arccos x 、反正切函数 y = arctan x 和反余切函数 y = arc cot x 等.它们的图形如图 1-5 所示. 图 1-3 图 1-4
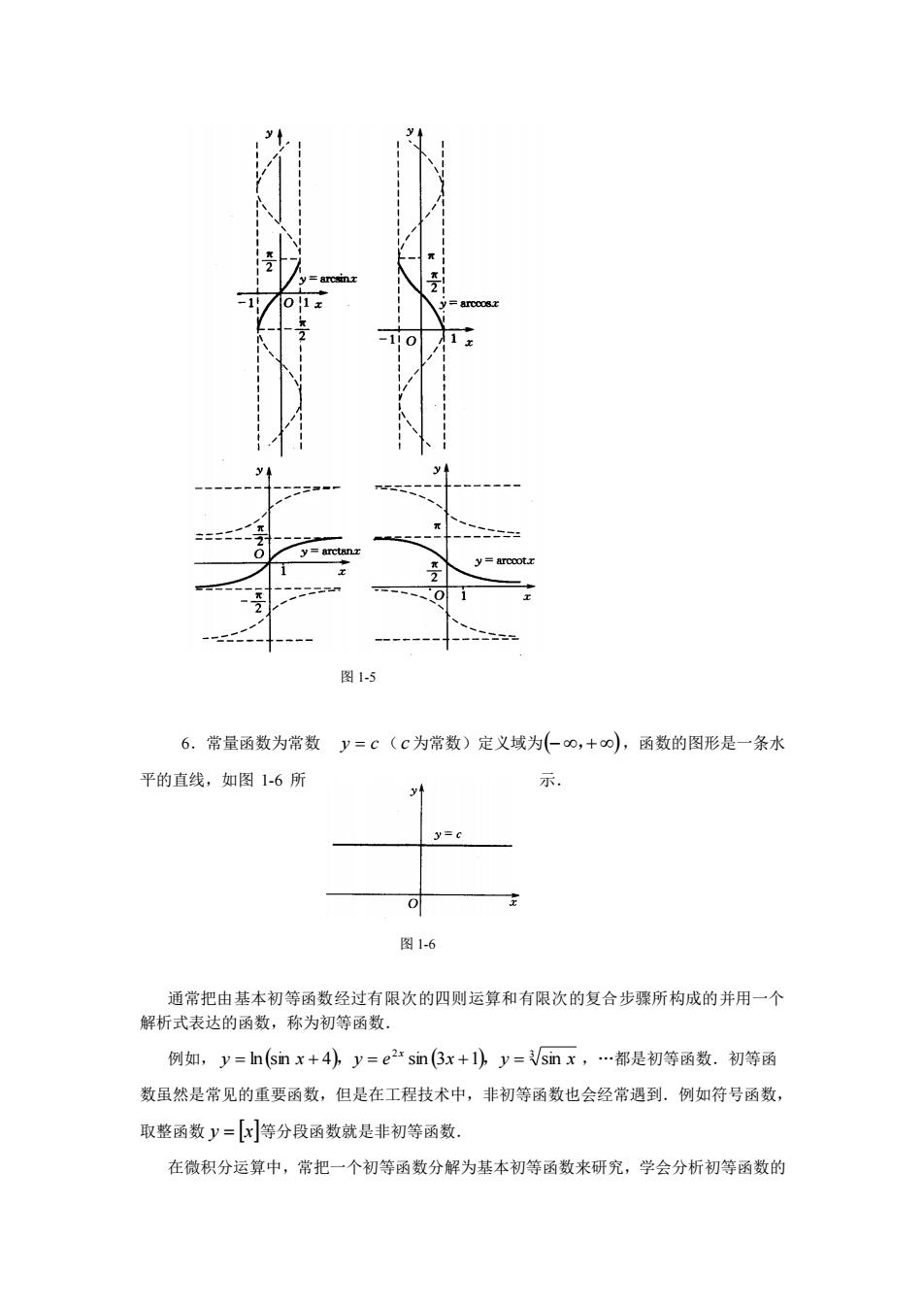
图15 6.常量函数为常数y=c(c为常数)定义域为(0,+0),函数的图形是一条水 平的直线,如图1-6所 y y=c 图1-6 通常把由基本初等函数经过有限次的四则运算和有限次的复合步骤所构成的并用一个 解析式表达的函数,称为初等函数. 例如,y=hsnx+4)y=e2sn(3x+)y=snx,.都是初等函数.初等函 数虽然是常见的重要函数,但是在工程技术中,非初等函数也会经常遇到。例如符号函数 取整函数y=[]等分段函数就是非初等函数。 在微积分运算中,常把一个初等函数分解为基本初等函数来研究,学会分析初等函数的
6.常量函数为常数 y = c ( c 为常数)定义域为 (−,+ ) ,函数的图形是一条水 平的直线,如图 1-6 所 示. 通常把由基本初等函数经过有限次的四则运算和有限次的复合步骤所构成的并用一个 解析式表达的函数,称为初等函数. 例如, ( ) ( ) 2 3 y ln sin x 4 y e sin 3x 1 y sin x x = + , = + , = ,.都是初等函数.初等函 数虽然是常见的重要函数,但是在工程技术中,非初等函数也会经常遇到.例如符号函数, 取整函数 y = x 等分段函数就是非初等函数. 在微积分运算中,常把一个初等函数分解为基本初等函数来研究,学会分析初等函数的 图 1-5 图 1-6