
第六为 第三章 强数图形的描给 一、曲线的渐近线 二、函数图形的描绘 Oaoo⊙⑧
第六节 一、 曲线的渐近线 二、 函数图形的描绘 机动 目录 上页 下页 返回 结束 函数图形的描绘 第三章

一、曲线的渐近线 定义.若曲线C上的点M沿着曲线无限地远离原点 时,点M与某一直线L的距离趋于0,则称直线L为 曲线C的渐近线 y=f(x) 或为“纵坐标差” M 夕=kx+b 例如,双曲线 x2 2 a b21 有新近线 x±=0 a b 但抛物线y=x2无渐近线 Oooo⊙o8
无渐近线 . 点 M 与某一直线 L 的距离趋于 0, 一、 曲线的渐近线 定义 . 若曲线 C上的点M 沿着曲线无限地远离原点 时, 则称直线 L 为 曲线C 的渐近线 . 例如, 双曲线 有渐近线 = 0 b y a x 但抛物线 或为“纵坐标差” N L y = k x +b M x y o C y = f (x) P x y o 机动 目录 上页 下页 返回 结束
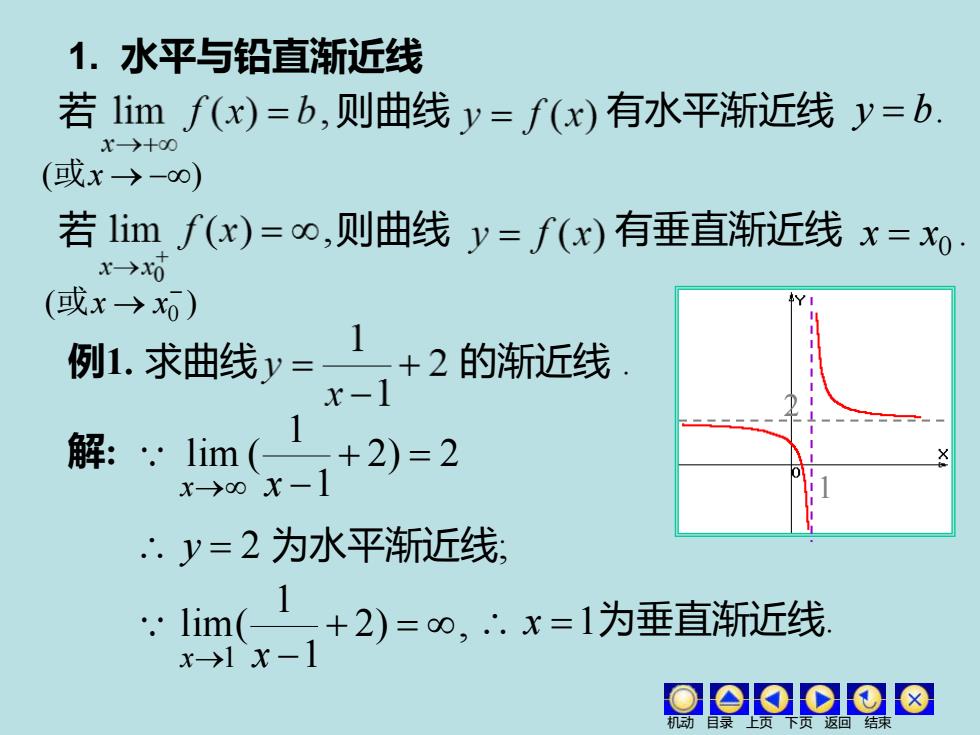
1.水平与铅直渐近线 若1imf(x)=b,则曲线y=f(x)有水平渐近线y=b. X→+00 (或x→-0) 若1imf(x)=o,则曲线y=f(x)有垂直渐近线x=x: x→x0 (或x→x0) 例1,求曲线y=1 +2的渐近线 -1 解::1m(1+2)=2 x→0x-1 ∴.y=2为水平渐近线 1 :1im(,+2)=o,∴.x=1为垂直渐近线 x→1x-1
1. 水平与铅直渐近线 若 则曲线 有水平渐近线 y = b. (或x → −) 若 则曲线 有垂直渐近线 . 0 x = x ( ) 0 → − 或x x 例1. 求曲线 的渐近线 . 解: 2) 2 1 1 lim ( + = x→ x − y = 2 为水平渐近线; 2) , 1 1 lim( 1 + = x→ x − x =1 为垂直渐近线. 2 1 机动 目录 上页 下页 返回 结束

2.斜渐近线(P75题13) 若1im[f(x)-(kx+b)]=0,则曲线y=f(x)有 X>+00 (或x→-0) 斜新近线y=kx+b. lim [f(x)-(kx+b)]=0 X>+00 ↓ k=1im/)_b] X→+00 lim对/ 2-k 61=0 k=lim f(x) x→十00 x (或x>-0) lim b]=0 b=lim [f(x)-kx] X→+00 (或x→-0) OAo⊙o8
2. 斜渐近线 斜渐近线 y = kx + b. (或x → −) 若 (kx + b) ] 0 ( ) lim [ − − = →+ x b k x f x x x (kx + b) ] 0 ( ) lim [ − − = →+ x b k x f x x ] ( ) lim [ x b x f x k x = − →+ x f x k x ( ) lim →+ = b lim [ f (x) kx] x = − →+ 机动 目录 上页 下页 返回 结束 (或x → −) (或x → −) ( P75 题13)
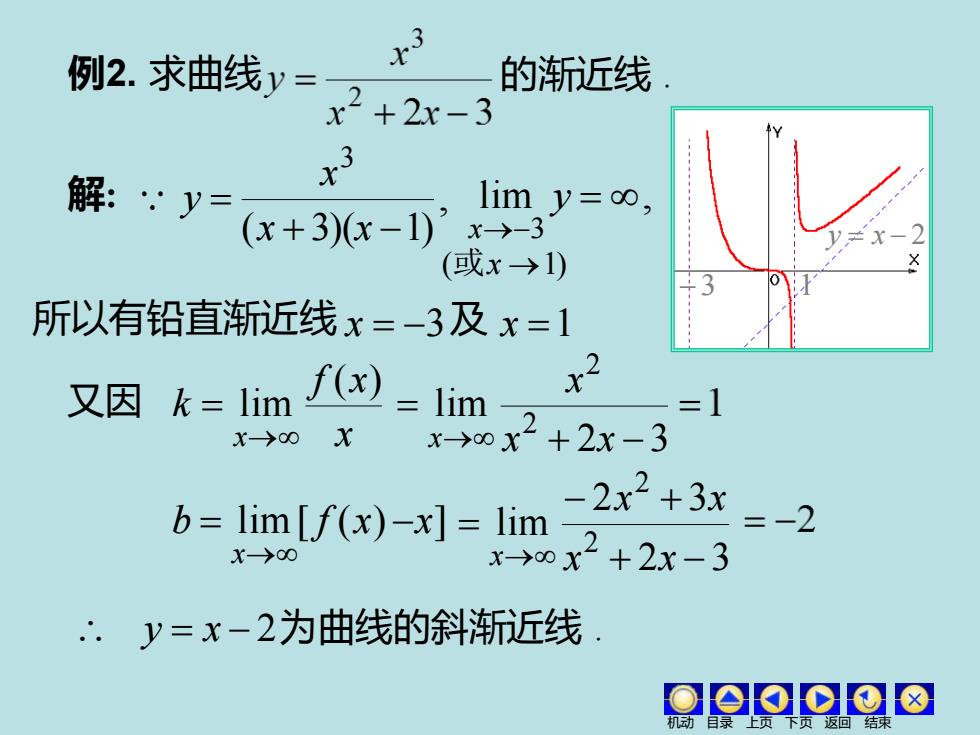
例2.求曲线y 的渐近线 x2+2x-3 解:y= x lim y=oo, (x+3)x-1)’x-→-3 (或x→1) 3 所以有铅直新近线x=-3及x=1 又因k=1imf)=lim x2 =1 x→00X x→0x2+2x-3 b=lim [f(x)-x]=lim- -2x2+3x =-2 X→00 0x2+2.x-3 ∴.y=x-2为曲线的斜渐近线
例2. 求曲线 的渐近线 . 解: , ( 3)( 1) 3 + − = x x x y lim , 3 = →− y x (或x →1) 所以有铅直渐近线 x = −3 及 x =1 又因 x f x k x ( ) lim → = 2 3 lim 2 2 + − = → x x x x b lim[ f (x) x] x = − → 2 3 2 3 lim 2 2 + − − + = → x x x x x y = x − 2为曲线的斜渐近线 . 机动 目录 上页 下页 返回 结束 −3 1 y = x − 2

二、函数图形的描绘 步骤: 1.确定函数y=f(x)的定义域,并考察其对称性及周 期性; 2.求f'(x),"(x),并求出f'(x)及f"(x)为0和不存在 的点; 3.列表判别增减及凹凸区间,求出极值和拐点, 4.求渐近线; 5.确定某些特殊点,描绘函数图形 OAo⊙o8
二、函数图形的描绘 步骤 : 1. 确定函数 的定义域 , 期性 ; 2. 求 并求出 及 3. 列表判别增减及凹凸区间 , 求出极值和拐点 ; 4. 求渐近线 ; 5. 确定某些特殊点 , 描绘函数图形 . 为 0 和不存在 的点 ; 并考察其对称性及周 机动 目录 上页 下页 返回 结束

例3.描绘y=}x3-x2+2的图形 解:1)定义域为(-oo,+∞),无对称性及周期性 2)y=x2-2x,y”=2x-2, 令y=0,得x=0,2 令y”=0,得x=1 3)x (-00,0) 0 (0,1) 1 (1,2) 12 (2,+0) + 0 0 0 十 + y 2 4 23 3 (极大) (拐点 (极小) 4) 3 2
例3. 描绘 的图形. 解: 1) 定义域为 无对称性及周期性. 2) 2 , 2 y = x − x y = 2x − 2, 令 y = 0, 令 y = 0, 3) x y y y (−,0) 0 (0,1) 1 (1,2) 2 (2,+ ) + 0 − − 0 + − − + + 2 3 4 (极大) (拐点) 3 2 (极小) 4) x y −1 3 3 2 2 0 机动 目录 上页 下页 返回 结束 −1 1 2 3

例4.描绘方程(-3)2+4y-4xy=0的图形 解:1)少=x-32 4x-定义域为(-∞,1),(1,+0) 2)求关键点 ·2(x-3)+4y-4y-4xy'=0 ·y=-x-3-2y=c-3)0x+1) 2(x-1) 4(x-1)2 .·2+4y"-8y'-4xy”=0 2 2(x-1)(x-103 令y=0得x=-1,3; OAo⊙o8
例4. 描绘方程 的图形. 解: 1) , 4( 1) ( 3) 2 − − = x x y 定义域为 2) 求关键点 2(x −3) + 4y − 4y − 4xy = 0 2( 1) 3 2 − − − = x x y y 2 + 4y −8y − 4xy = 0 2( 1) 1 4 − − = x y y 令 y = 0得 x = −1, 3; 机动 目录 上页 下页 返回 结束

3)判别曲线形态 (-0,-1)-1(-1,1) 1 (1,3) 3 (3,+0) 0 0 + 无定义 十 -2 0 (极大) (极小少 4)求渐近线 .limy=oo,.x=1为铅直渐近线 x-→1 (x-3)2 y=x-3x+) 2 4(x-1) 4(x-1)7 (x-1) Qb地⑧
x (−,−1) −1 (−1,1) 1 (1,3) 3 (3,+ ) y y y + − − + − − + + − 2 0 , 4( 1) ( 3) 2 − − = x x y , 4( 1) ( 3)( 1) 2 − − + = x x x y 3 ( 1) 2 − = x y 3) 判别曲线形态 0 0 (极大) (极小) 4) 求渐近线 lim , 1 = → y x 为铅直渐近线 无 定 义 机动 目录 上页 下页 返回 结束 x =1

又因 lim=1 即k- x→0X 4 车my灯=m-8 X→00 x→04(x-1) -5x+95 lim x-→04(x-1) 4 (x-3)2 小为斜斯新近线 4(x-10 5 /=(x-3ax+1) 4(x-1)2 5)求特殊点 0 2 9 1 2 y 4 4 x-1)月 oooo08
又因 x y x→ lim , 4 1 = 4 1 即 k = ) 4 1 b lim ( y x x = − → ] 4 1 4( 1) ( 3) lim[ 2 x x x x − − − = → 4( 1) 5 9 lim − − + = → x x x 4 5 = − 4( 1) ( 3) 2 − − = x x y 5) 求特殊点 x y 0 4 9 − 2 4 1 为斜渐近线 4 5 4 1 y = x − 机动 目录 上页 下页 返回 结束 2 4( 1) ( 3)( 1) − − + = x x x y 3 ( 1) 2 − = x y