第七为 第三章 平面曲我的曲 曲线的弯 与切线的转角有关 曲程度 与曲线的弧长有关 M M 主要内容: 一、 孤微分 二 曲率及其计算公式 三、 曲率圆与曲率半径 OAo⊙o8
第七节 曲线的弯 曲程度 与切线的转角有关 与曲线的弧长有关 机动 目录 上页 下页 返回 结束 主要内容: 一、 弧微分 二、 曲率及其计算公式 三、 曲率圆与曲率半径 M M M 平面曲线的曲率 第三章
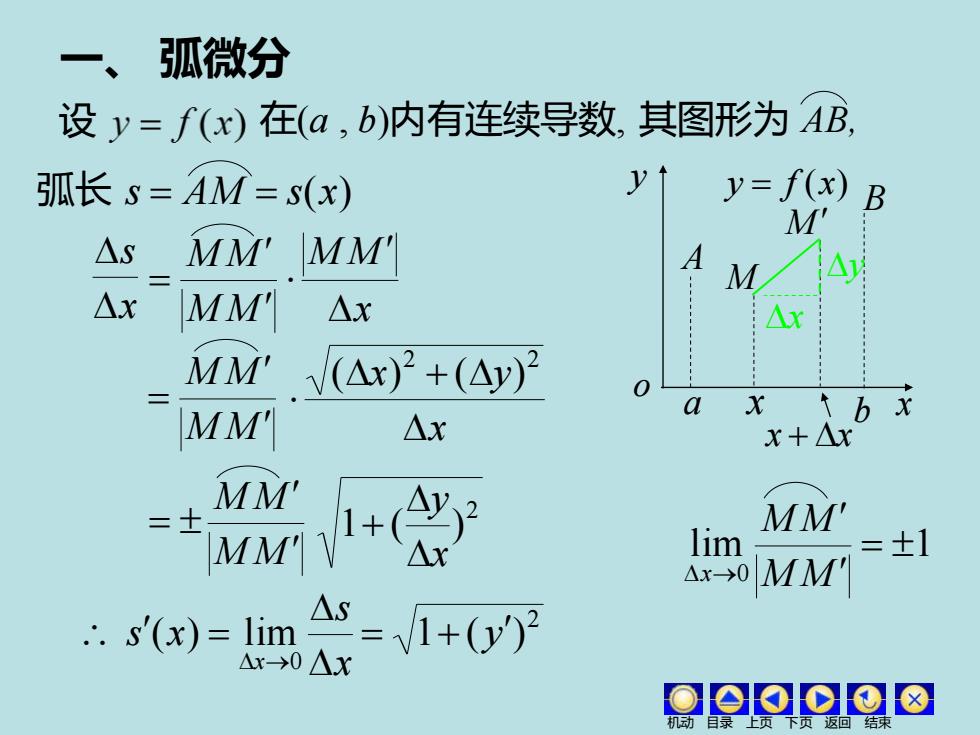
一、弧微分 设y=f(x)在(a,b)内有连续导数,其图形为AB, 弧长S=AM=s(x) y=f( )B M' △S MM MM' A M △x MM' △x MM' V(△x)2+(△y)2 a MM' △x X↑bx x+△x MM MM' lim =±1 Ax0MM' .s'(x)=lim
一、 弧微分 设 在(a , b)内有连续导数, 其图形为 AB, 弧长 s = AM = s(x) x s M M M M = x M M M M M M = x x y + 2 2 ( ) ( ) M M M M = 2 1 ( ) x y + x s s x x = →0 ( ) lim 2 = 1+ ( y ) x A B y = f (x) a b x o y x M x + x M y lim 1 0 = → M M M M x 机动 目录 上页 下页 返回 结束

s'(x)=1+(y)2 .ds=+)2dx ds=/(dx)2+(dy)2 若曲线由参数方程表示 x=) y=y(t) 则弧长微分公式为ds=2+2dt 几何意义: ds =MT dx dy dx cosa sina ds ds xx+dx x @Oo⊙⊙8
则弧长微分公式为 ds x y d t 2 2 = + ds 1 ( y ) dx 2 = + 或 2 2 ds = (dx) + (dy) x + dx dx o x y x M dy T 几何意义: ds = MT cos ; d d = s x sin d d = s y 若曲线由参数方程表示: = = ( ) ( ) y y t x x t 机动 目录 上页 下页 返回 结束

二、曲率及其计算公式 在光滑弧上自点M开始取弧段,其长为△、,对应切线 转角为△a,定义 弧段△s上的平均曲率 K= △0 M △s 点M处的曲率 △ da K=lim △s-→0 △S ds 注意:直线上任意点处的曲率为0! OaoO⊙8
二、曲率及其计算公式 在光滑弧上自点 M 开始取弧段, 其长为 s , 对应切线 , 定义 弧段 s 上的平均曲率 s K = M M s 点 M 处的曲率 s K s = → 0 lim ds d = 注意: 直线上任意点处的曲率为 0 ! 机动 目录 上页 下页 返回 结束 转角为

例1.求半径为R的圆上任意点处的曲率 解:如图所示, △S=R△0 AaAs △ R、 ∴.K=lim △S→0 R 可见:R愈小,则K愈大,圆弧弯曲得愈厉害; R愈大,则K愈小,圆弧弯曲得愈小. OAo⊙o8
例1. 求半径为R 的圆上任意点处的曲率 . 解: 如图所示 , s = R s K s = → 0 lim R 1 = 可见: R 愈小, 则K 愈大 , 圆弧弯曲得愈厉害 ; R 愈大, 则K 愈小 , 圆弧弯曲得愈小 . s R M M 机动 目录 上页 下页 返回 结束

曲率K的计算公式 d K= 设曲线弧y=f(x)二阶可导,则由 ds anu=y(设-7ca<3 得 a arctan y' der (nuchayd 又ds=1+y2dx 故曲率计算公式为K y" (1+y2)3 当y<1时,有曲率近似计算公式K≈y” oaoo®8
当 y 1时, 有曲率近似计算公式 tan = y ) 2 2 ( 设 − 得 = arctan y d = (arctan y )dx 故曲率计算公式为 s K d d = 2 3 (1 ) 2 y y K + = K y 又 曲率K 的计算公式 设曲线弧 y = f (x) 二阶可导, 则由 机动 目录 上页 下页 返回 结束

说明: x=x(t) (1)若曲线由参数方程 给出,则 y=y(t) K= (2+2)形 (2)若曲线方程为x=(y),则 x" K- (1+x2)形 K- y" (1+y2)3 oeo0
说明: (1) 若曲线由参数方程 = = ( ) ( ) y y t x x t 给出, 则 2 3 (1 ) 2 y y K + = (2) 若曲线方程为 x =(y), 则 2 3 (1 ) 2 x x K + = 2 3 ( ) 2 2 x y xy xy K + − = 机动 目录 上页 下页 返回 结束

例2.我国铁路常用立方抛物线y=x3作缓和曲线, 6R1 其中R是圆弧弯道的半径,1是缓和曲线的长度,且1<<R 求此缓和曲线在其两个端点00,0),B1,6R 处的曲率 说明: 铁路转弯时为保证行车 平稳安全,离心力必须 连续变化,因此铁道的 曲率应连续变化. 点击图片任意处播放暂停 ololotolol8
例2. 我国铁路常用立方抛物线 3 6 1 x Rl y = 作缓和曲线, 处的曲率. 点击图片任意处播放\暂停 说明: 铁路转弯时为保证行车 平稳安全, 求此缓和曲线在其两个端点 机动 目录 上页 下页 返回 结束 其中R是圆弧弯道的半径, l 是缓和曲线的长度, 且 l << R. 离心力必须 连续变化 , 因此铁道的 曲率应连续变化
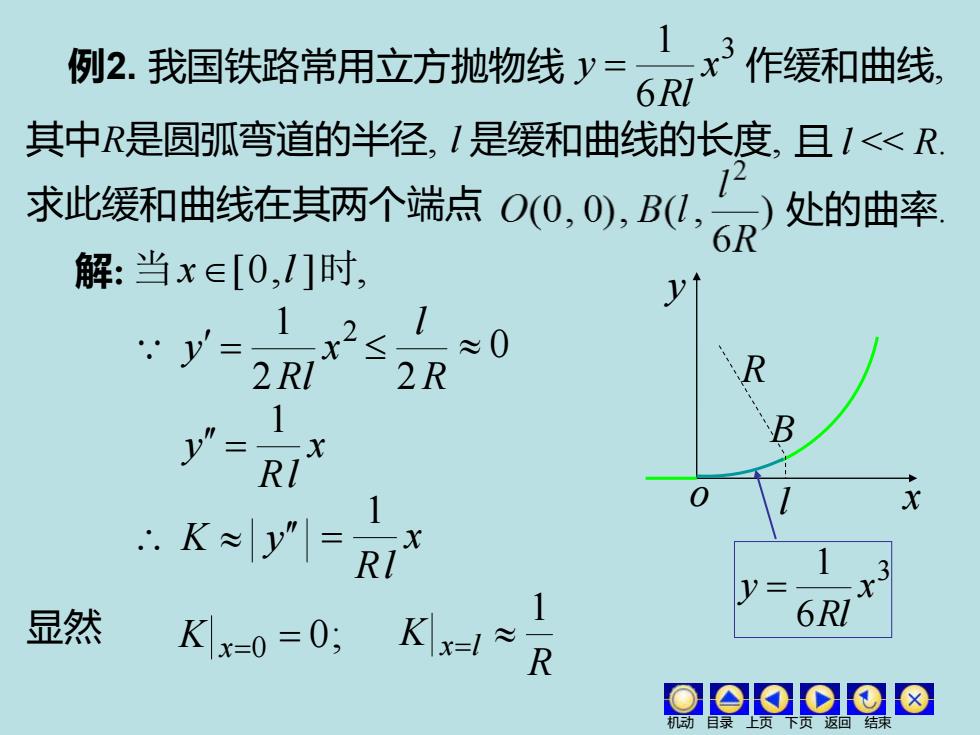
例2.我国铁路常用立方抛物线y= 作缓和曲线, 6RI 其中R是圆弧弯道的半径,1是缓和曲线的长度,且1<<R. 求此缓和曲线在其两个端点00,0),B0,6R处的曲率 解:当x∈[0,l]时 .y= ≈0 2R y”= 1 RI X .K≈y 显然 6RI Kx=0=0 oeo0
例2. 我国铁路常用立方抛物线 3 6 1 x Rl y = 作缓和曲线, 且 l << R. 处的曲率. 其中R是圆弧弯道的半径, l 是缓和曲线的长度, 求此缓和曲线在其两个端点 机动 目录 上页 下页 返回 结束 解: 当x[0,l ]时, R l 2 0 x Rl y 1 = K y x Rl 1 = 显然 0; K x=0 = R K x l 1 = 2 2 1 x Rl y = R B y o x 3 6 1 x Rl y = l

x=acost 例3.求椭圆 (0≤t≤2π)在何处曲率最大? y=bsint 解:x=-asint; =-acost 礻表示对参 =bcost; =-bsint 数t的导数 故曲率为 K 护-的 ab (2+2)为 (a2sin2t+b2cos2t) K最大=f)=a2sin2t+b2cos2t最小 求驻点 f'(t)=2a2sintcost-2bcostsint=(a2-b2)sin2t Ooo⊙o☒
例3. 求椭圆 在何处曲率最大? 解: 故曲率为 = ab 2 3 ( sin cos ) 2 2 2 2 a t + b t x = −asint; y = bcost; x = −acost y = −bsint 2 3 ( ) 2 2 x y xy xy K + − = K 最大 f t a t b t 2 2 2 2 ( ) = sin + cos 最小 机动 目录 上页 下页 返回 结束 f (t) 2a sint cost 2bcostsint 2 = − (a b )sin 2t 2 2 = − 求驻点: 数 的导数 表示对参 t x