
第四为 第三章 岛数的单调性与 曲孩的凹凸性 一、函数单调性的判定法 二、曲线的凹凸与拐点 Oo▣⊙08 机无
第四节 一、函数单调性的判定法 机动 目录 上页 下页 返回 结束 二、曲线的凹凸与拐点 函数的单调性与 曲线的凹凸性 第三章

函数单调性的判定法 定理1.设函数f(x)在开区间I内可导,若f'(x)>0 (∫'(x)0,x∈I,任取1,x2∈I(0 5∈(,x2)c1 故f(:)<f(x2).这说明f(x)在I内单调递增 证毕 ▣ao⊙o8
一、 函数单调性的判定法 定理 1. 设函数 若 ( f (x) 0), 则 在 I 内单调递增 (递减) . 证: 无妨设 任取 由拉格朗日中值定理得 0 故 这说明 在 I 内单调递增. 在开区间 I 内可导, 机动 目录 上页 下页 返回 结束 证毕

例1.确定函数f(x)=2x3-9x2+12x-3的单调区间 解:f'(x)=6x2-18x+12=6(x-1)(x-2) 令f'(x)=0,得x=1,x=2 (-0,1)1(1,2) (2,+0) f'(x) 十 0 0 f(x) 2 故f(x)的单调增区间为(-0,1),(2,+o): f(x)的单调减区间为(1,2) 12 Oo▣⊙⊙8
例1. 确定函数 的单调区间. 解: ( ) 6 18 12 2 f x = x − x + = 6(x −1)(x − 2) 令 f (x) = 0 , 得 x =1, x = 2 x f (x) f (x) (−,1) 2 0 0 1 (1, 2) (2, + ) + − + 2 1 故 的单调增区间为 (−,1), (2, + ); 的单调减区间为 (1, 2). 1 2 o x y 1 2 机动 目录 上页 下页 返回 结束

说明: 1)单调区间的分界点除驻点外,也可是导数不存在的点 例如,y=√x2,x∈(-o0,+o0) yy=x2 2 -33元 yx=0=0 0 2)如果函数在某驻点两边导数同号, 则不改变函数的单调性 例如,y=x3,x∈(-0,+0) y'=3x2 y=0=0
y o x 说明: 1) 单调区间的分界点除驻点外,也可是导数不存在的点. 例如, 3 2 y = x 2) 如果函数在某驻点两边导数同号, 则不改变函数的单调性 . 例如, y o x 3 y = x 机动 目录 上页 下页 返回 结束

例2.证明O<x<时,成立不等式sinx 2 证:令f(x)= sinx 2 X π 则f()在(0,牙1上连续,在(0,上可导,且 x2 x2(x-tanx)<0 f(x)=cosx-sinx _cos 证 因此f)在(0,)内单调递减, tan x 又f(9)在7处左连续,因此f()≥f兮)=0 从而 ss xe(0.) Oo▣⊙⊙8
例2. 证明 时, 成立不等式 证: 令 , sin 2 ( ) = − x x f x 2 cos sin ( ) x x x x f x − = ( tan ) cos 2 x x x x = − 1 tan x x 0 从而 因此 且 证 证明 目录 上页 下页 返回 结束

二、曲线的凹凸与拐点 定义.设函数f(x)在区间I上连续,x1,2∈I, 若恒有)f)+f),则称f的 2 图形是凸的 y 连续曲线上有切线的凹凸分界点 称为拐点
A B 定义 . 设函数 在区间 I 上连续 , (1) 若恒有 则称 图形是凹的; (2) 若恒有 则称 连续曲线上有切线的凹凸分界点 称为拐点 . 图形是凸的 . y o x1 x2 x 2 1 2 x +x y o x1 x 2 1 2 x +x 2 x y o x 二、曲线的凹凸与拐点 机动 目录 上页 下页 返回 结束

定理2.(凹凸判定法)设函数f(x)在区间1上有二阶导数 (1)在1内∫"(x)>0,则f(x)在I内图形是凹的,+ (2)在1内f"(x)0时,12≥fě ,说明(1)成立 (2) 证毕 Qoo⊙⊙8
定理2.(凹凸判定法) (1) 在 I 内 则 在 I 内图形是凹的 ; (2) 在 I 内 则 在 I 内图形是凸的 . + − 证: 利用一阶泰勒公式可得 ( ) ( ) 1 f x = f 2 1 2 x + x 2! ( ) 1 f + 2 1 (x − ) 2 1 2 x + x ( ) ( ) 2 f x = f 2 1 2 x + x + f ( ) 2 1 2 x + x ( ) x2 − 2 1 2 x + x 2! ( ) 2 f + 2 2 (x − ) 2 1 2 x + x 两式相加 ( ) ( ) 2 ( ) 1 2 f x + f x = f 2 1 2 x + x 2 2! 2 1 ( ) 2 1 x −x + [ ( ) ( )] 1 2 f + f 当f (x) 0时, ( ), 2 ( ) ( ) 1 2 f f x f x + 2 1 2 x + x 说明 (1) 成立; (2) + f ( ) 2 1 2 x + x ( ) 1 x 2 1 2 x + x 机动 目录 上页 下页 返回 结束 设函数 在区间I 上有二阶导数 证毕

例3.判断曲线y=x的凹凸性 解:y'=4x3,y”=12x2 当x≠0时,y”>0;x=0时,y”=0 故曲线y=x4在(-o0,+o)上是向上凹的. 说明: 1)若在某点二阶导数为0,在其两侧二阶导数不变号, 则曲线的凹凸性不变 2)根据拐点的定义及上述定理,可得拐点的判别法如下: 若曲线y=f(x)在点xo连续,∫"(xo)=0或不存在, 但∫"(x)在x两侧异号,则点(x,f(xo)》是曲线 y=∫(x)的一个拐点
例3. 判断曲线 的凹凸性. 解: 4 , 3 y = x 故曲线 在 上是向上凹的. 说明: 1) 若在某点二阶导数为 0 , 2) 根据拐点的定义及上述定理, 可得拐点的判别法如下: 若曲线 或不存在, 但 f (x) 在 两侧异号, 0 x 则点 ( , ( )) 0 0 x f x 是曲线 的一个拐点. 则曲线的凹凸性不变 . 在其两侧二阶导数不变号, x y o 机动 目录 上页 下页 返回 结束

例4.求曲线y=x的拐点 解y=x,y=-x为 (-00,0) 0 (0,+00) + 不存在 y 凹 0 凸 因此点(0,0)为曲线y=x的拐点 QOo⊙⊙8
例4. 求曲线 的拐点. 解: , 3 2 3 1 − y = x 3 5 9 2 − y = − x x y y (−,0) 0 (0,+ ) 不存在 0 + − 因此点 ( 0 , 0 ) 为曲线 的拐点 . 凹 凸 机动 目录 上页 下页 返回 结束
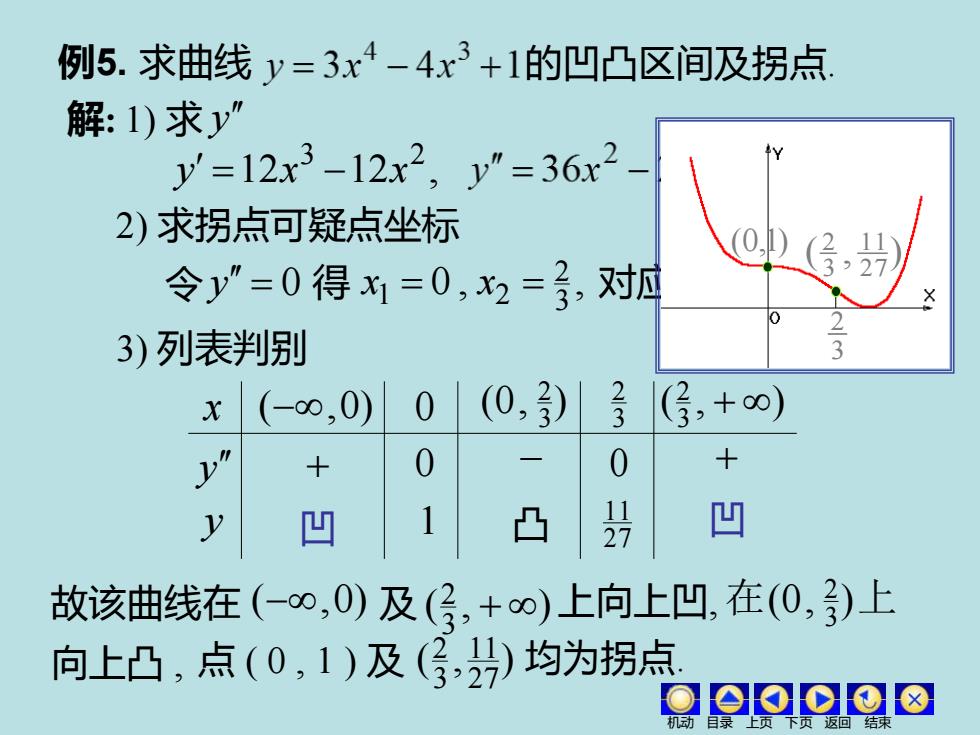
例5.求曲线y=3x4-4x3+1的凹凸区间及拐点 解:1)求y” y=12x3-12x2,y”=36x2 2)求拐点可疑点坐标 令y”=0得1=0,x2=号,对应 327 3)列表判别 x (-00,0) 0 (0,) 23 (3,+o) + 0 0 + y 凹 凸 27 凹 故该曲线在(-0,0)及(?,+0)上向上凹,在(0,)上 向上凸,点(0,1)及(号,)均为拐点
36 ( ) 3 2 = x x − 例5. 求曲线 的凹凸区间及拐点. 解: 1) 求 y 12 12 , 3 2 y = x − x 2) 求拐点可疑点坐标 令 y = 0 得 0 , , 3 2 x1 = x2 = 对应 3) 列表判别 27 11 1 2 y =1, y = (−,0) (0, ) 3 2 ( , ) 3 2 + y x y 0 3 2 + 0 0 1 27 11 − + 故该曲线在 (−,0) ( , ) 3 及 2 + 上向上凹, 向上凸 , 点 ( 0 , 1 ) 及 ( , ) 27 11 3 2 均为拐点. 在(0, 3 2 )上 凹 凸 凹 机动 目录 上页 下页 返回 结束 3 2 (0,1) ( , ) 27 11 3 2