
第二为 第四章 换无积分法 一、第一类换元法 二、第二类换元法 Oo▣⊙⊙8 机
二、第二类换元法 第二节 一、第一类换元法 机动 目录 上页 下页 返回 结束 换元积分法 第四章

基本思路 设F'(u)=f(W),u=p(x)可导,则有 dFLo(x)]=fo(x)]o'(x)dx ∴.∫fp(xp'(x)dc=F[p(x]+C=F(u+Cu=px) =∫f(u)dlu=o(x) 第一类换元法 ∫flp(r]p'()dr 第二类换元法 ∫f(o)du Qao⊙o&
第二类换元法 第一类换元法 基本思路 机动 目录 上页 下页 返回 结束 设 F(u) = f (u), 可导, F[(x)]+C d ( ) ( ) u u u x f = = ( ) ( ) = F u +C u= x dF[(x)] = f [(x)](x)dx 则有

一、第一类换元法 定理1.设f(w)有原函数,u=p(x)可导,则有换元 公式 j/Lo(vp'cxdr=jfuilu=o() 即 「fLp(x)]p'(x)dx=∫f(o(x)dp(x) (也称配元法,凑微分法) Oo▣⊙O8 机
一、第一类换元法 定理1. 设 f (u)有原函数, u =(x)可导, 则有换元 公式 f (u)du u =(x) f ((x))d(x) (也称配元法 即 = f [(x)] (x)dx , 凑微分法) 机动 目录 上页 下页 返回 结束

例1.求∫(ax+b)"dc(m≠-1), 解:令u=ax+b,则du=adx,故 原式=∫w”dw=1.1 m+1+C 0 m+1 a a(m T(bC 注:当m=-1时 jbnar+4+c Qo⊙⊙8
例1. 求 解: 令 u = ax + b , 则 d u = adx , 故 原式 = m u u a d 1 a 1 = u C m m + + +1 1 1 注: 当 时 机动 目录 上页 下页 返回 结束

2.求∫ dx 想到公式 2+x2 du dx arctan u+C 令w ,则du=dx a a Laretan()+C Oo▣⊙08 机
+ = 2 2 1 ( ) 1 d a x x a 例2. 求 解: , a x 令 u = 则 x a u d 1 d = + 2 1 u du a 1 u C a = arctan + 1 想到公式 + 2 1 d u u = arctan u +C ( ) a x = 机动 目录 上页 下页 返回 结束

dx 小g dx arcsin+C a 想到 du arcsinu+C ∫f[(x]p'(xdr=∫f((x)do(x) (直接配元)
例3. 求 = − 2 1 d u u 想到 arcsinu +C 解: − 2 1 ( ) d a x a x = f ((x))d(x) (直接配元) f [(x)] (x)dx − = 2 1 ( ) d ( ) a x a x 机动 目录 上页 下页 返回 结束
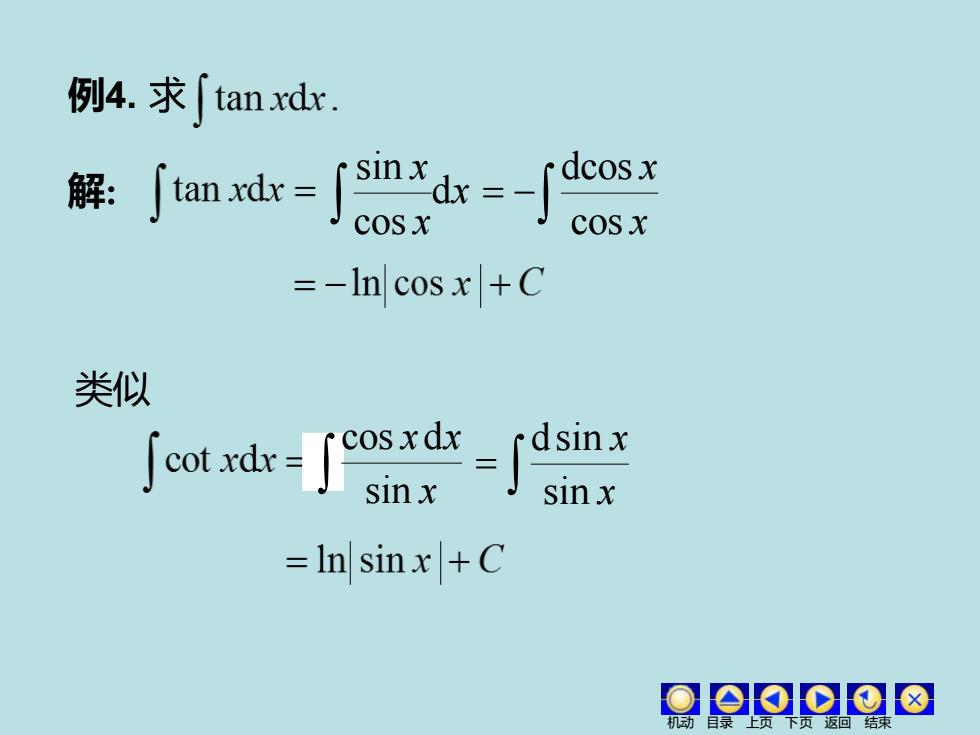
例4.求∫tanxdx 屏j如咖-品=j =-In cos x +C 类似 eod d sin x =In sinx +C Oo▣⊙08
例4. 求 解: x x x d cos sin = − x x cos dcos x x x sin cos d = x x sin dsin 机动 目录 上页 下页 返回 结束 类似

5.求2a2 dx 解: x2-a2 1(x+0)-x-0=1(1-1 2a (x-a)(x+a)2a x-a x+a 原赋=∫中a] =-j*2 -aaal-r+a小c-ah C x+a
C x a x a a + + − = ln 2 1 例5. 求 解: 2 2 1 x − a (x − a)(x + a) (x + a) − (x − a) 2a 1 = ) 1 1 ( 2 1 a x a x + a − − = ∴ 原式 = 2a 1 + − − x a x x a dx d = 2a 1 − − x a d(x a) 2a 1 = ln x − a − ln x + a +C + + − x a d(x a) 机动 目录 上页 下页 返回 结束

常用的几种配元形式: ([f(ax+bydx=f(ax+b)d(ax+b) (2jfx"xdx=Jfe")dx” 万能 o)jrer=ajrue)adr 法 (4)f(sinx)cos xdx=[f(sinx)dsinx (5)∫f(cos)sinxdx=-∫fcos)dcosx Oo▣⊙⊙8
常用的几种配元形式: + = (1) f (ax b)dx d(ax + b) a 1 = − f x x x n n (2) ( ) d 1 n dx n 1 = x x f x n d 1 (3) ( ) n dx n 1 n x 1 万 能 凑 幂 法 = (4) f (sin x)cos xdx dsin x = (5) f (cos x)sin xdx − dcos x 机动 目录 上页 下页 返回 结束

(6)∫f(tanx)sec2xdx=∫f(tanx)dtanx (7)∫fe*)e'dr=∫fe*)de 8)jf0 inx)dx=-∫f血)dnx 16.求x2n时 dx 解原式-j10。-2 n+2xi+C
= (6) f (tan x)sec xdx 2 dtan x = f e e x x x (7) ( ) d x de = x x f x d 1 (8) (ln ) dln x 例6. 求 1+ 2ln x dln x 解: 原式 = + = 2 1 2ln x 1 d(1+ 2ln x) 机动 目录 上页 下页 返回 结束