
第五章 定积分 不定积分 积分学 定积分
第五章 积分学 不定积分 定积分 定积分

第一为 第五章 定积分的桡念及性质 一、 定积分问题举例 二、 定积分的定义 三、定积分的性质 oeooo 机
第一节 一、定积分问题举例 二、 定积分的定义 三、 定积分的性质 机动 目录 上页 下页 返回 结束 定积分的概念及性质 第五章
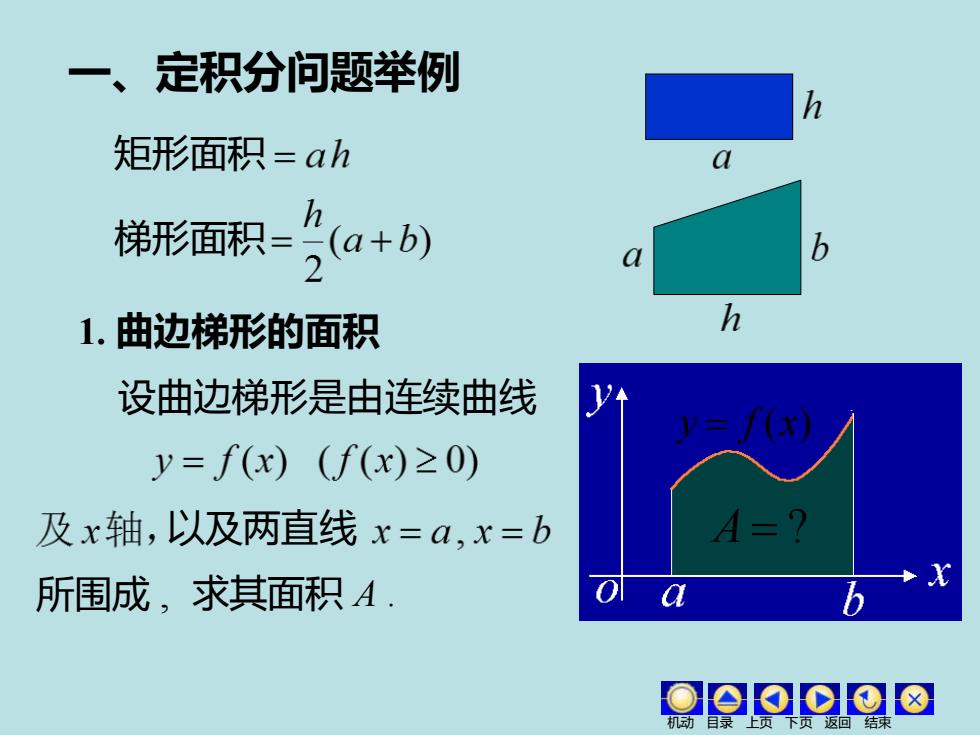
一、定积分问题举例 矩形面积=ah 锁形适限-含a+ 1.曲边梯形的面积 设曲边梯形是由连续曲线 v=/(x) y=f(x)(f(x)≥0) 及x轴,以及两直线x=a,x=b A=? 所围成,求其面积A. Oao⊙⊙☒
一、定积分问题举例 1. 曲边梯形的面积 设曲边梯形是由连续曲线 以及两直线 所围成 , 求其面积 A . A = ? 机动 目录 上页 下页 返回 结束 y = f (x) 矩形面积 梯形面积
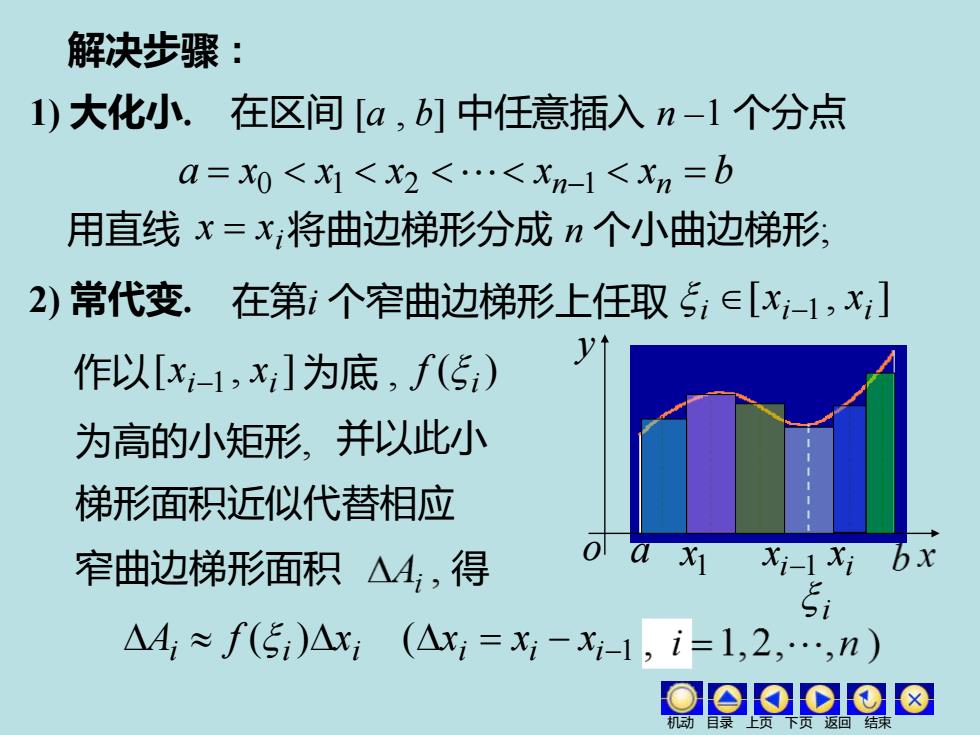
解决步骤: 1)大化小.在区间[a,b]中任意插入n-1个分点 a=0<1<X2<.<Xn-1<xn=b 用直线x=x;将曲边梯形分成n个小曲边梯形, 2)常代变.在第i个窄曲边梯形上任取5,∈[x;-1,x;] 作以[x-1,x]为底,f(5) 为高的小矩形,并以此小 梯形面积近似代替相应 窄曲边梯形面积△4,得 a x1 xi-1xi bx Si △4;≈f(5i)△x1(Ax=x1-Xi-1,i=1,2,.,n) OOo⊙o8
1 x i x i−1 a x y o 解决步骤 : 1) 大化小. 在区间 [a , b] 中任意插入 n –1 个分点 a = x0 x1 x2 xn−1 xn = b [ , ] i i 1 i x x − 用直线 i x = x 将曲边梯形分成 n 个小曲边梯形; 2) 常代变. 在第i 个窄曲边梯形上任取 作以 [ , ] i 1 i x x − 为底 , ( )i f 为高的小矩形, 并以此小 梯形面积近似代替相应 窄曲边梯形面积 得 ( ) ( ) i i i i = i − i−1 A f x x x x i 机动 目录 上页 下页 返回 结束
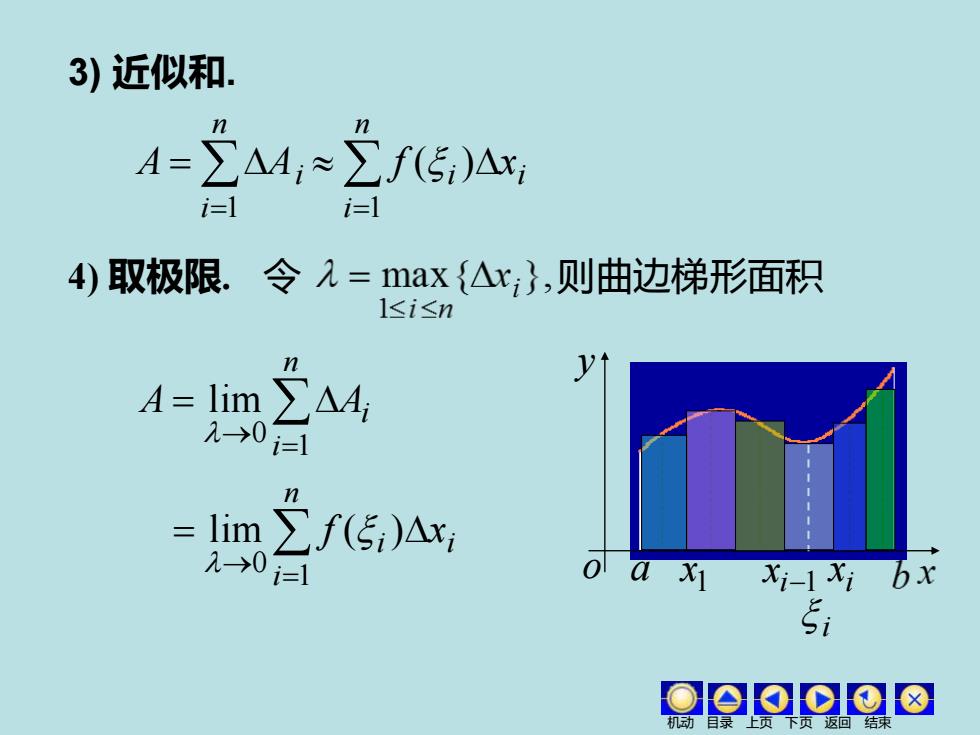
3)近似和. A=∑△4,≈∑f5)△x i=1 i=l 4)取极限.令2=max{△x},则曲边梯形面积 1≤i≤n 4=lim ∑A4 1→0 n =lim∑f(5i)△xi 2→01 a x 1Xi-1xb尤 si
3) 近似和. = = n i A Ai 1 = n i i i f x 1 ( ) 4) 取极限. 令 则曲边梯形面积 → = = n i A Ai 1 0 lim → = = n i i i f x 1 0 lim ( ) 机动 目录 上页 下页 返回 结束 a y o 1 x i x i−1 x i

2.变速直线运动的路程 设某物体作直线运动,已知速度v=v(t)∈CT1,T2],且 v()≥0,求在运动时间内物体所经过的路程s. 解决步骤: 1)大化小.在[T,T2]中任意插入n-1个分点,将它分成 n个小段[t-1,t](i=1,2,.,n),在每个小段上物体经 过的路程为△s;(i=1,2,.,n) 2)常代变.任取5∈[t;-1,t],以v(5)代替变速,得 △S≈v(5i)△ti(i=1,2,.,n) Ooo⊙⊙8 机
2. 变速直线运动的路程 设某物体作直线运动, 且 求在运动时间内物体所经过的路程 s. 解决步骤: 1) 大化小. 将它分成 在每个小段上物体经 2) 常代变. 得 i i i s v( )t (i =1, 2, ,n) 已知速度 机动 目录 上页 下页 返回 结束 n 个小段 过的路程为

3)近似和. S≈ ∑(5)△t i=l 4)取极限. s=lim∑v(5i)△t (2=max△t) 20i1 l≤i≤n 上述两个问题的共性 •解决问题的方法步骤相同: 大化小,常代变,近似和,取极限” ·所求量极限结构式相同: 特殊乘积和式的极限
3) 近似和. 4) 取极限 . 上述两个问题的共性: • 解决问题的方法步骤相同 : “大化小 , 常代变 , 近似和 , 取极限 ” • 所求量极限结构式相同: 特殊乘积和式的极限 机动 目录 上页 下页 返回 结束

二、定积分定义(P225) 设函数f(x)定义在[a,b]上,若对[a,b]的任一种分法 a=X0<为<x2<<xn=b,令△x;=x;-x;-1,任取 5:∈[x,x-1],只要=max{△x}→0时∑f(5)△x l≤i≤n i=l 总趋于确定的极限1,则称此极限I为函数∫(x)在区间 [a,b]上的定积分,记作∫f(x)dx 即」 rua=g2e 0☑xx-x,bx 此时称f(x)在[a,b]上可积 Ooo⊙⑨8
o a b x 二、定积分定义 ( P225 ) 任一种分法 , a = x0 x1 x2 xn = b 任取 i 总趋于确定的极限 I , 则称此极限 I 为函数 在区间 上的定积分, 1 x i x i−1 x b a f (x)dx 即 = b a f (x)dx i n i i f x → =1 0 lim ( ) 此时称 f ( x ) 在 [ a , b ] 上可积 . 记作 机动 目录 上页 下页 返回 结束
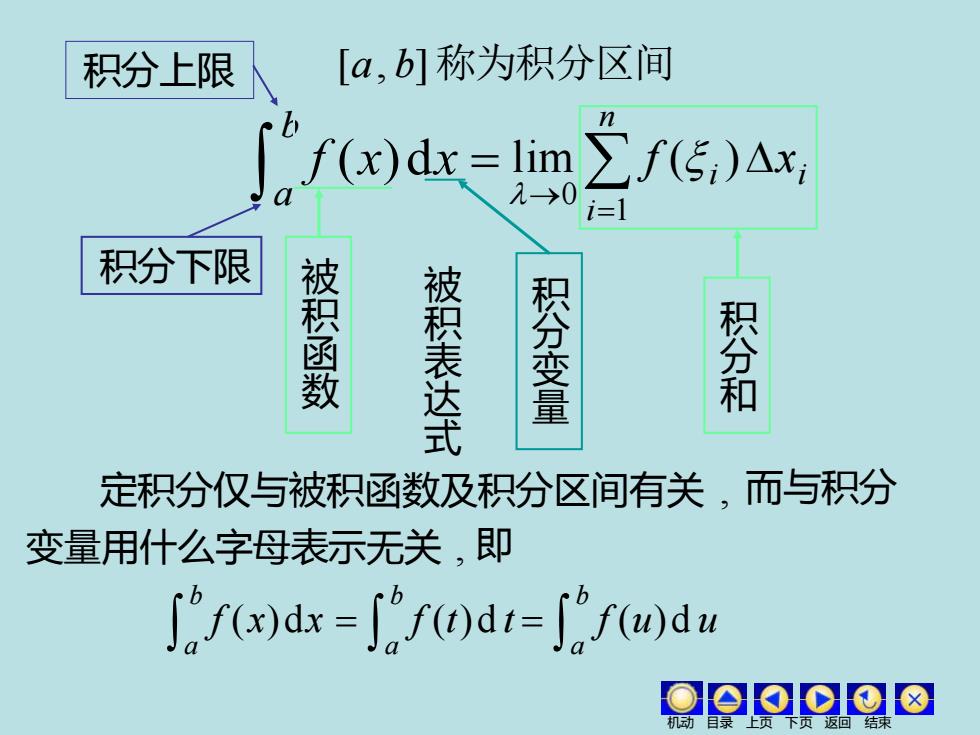
积分上限 [a,b]称为积分区间 f(x)dx=lim ∑f(5)△x, 2→0 i=1 积分下限 被积函数 被积表达式 积分变量 积分和 定积分仅与被积函数及积分区间有关,而与积分 变量用什么字母表示无关,即 -d-fd
= b a f (x)dx i n i i f x = → 1 0 lim ( ) 积分上限 积分下限 被 积 函 数 被 积 表 达 式 积 分 变 量 积 分 和 [a, b]称为积分区间 定积分仅与被积函数及积分区间有关 , 而与积分 变量用什么字母表示无关 , 即 b a f (x)dx = b a f (t)d t = b a f (u)d u 机动 目录 上页 下页 返回 结束
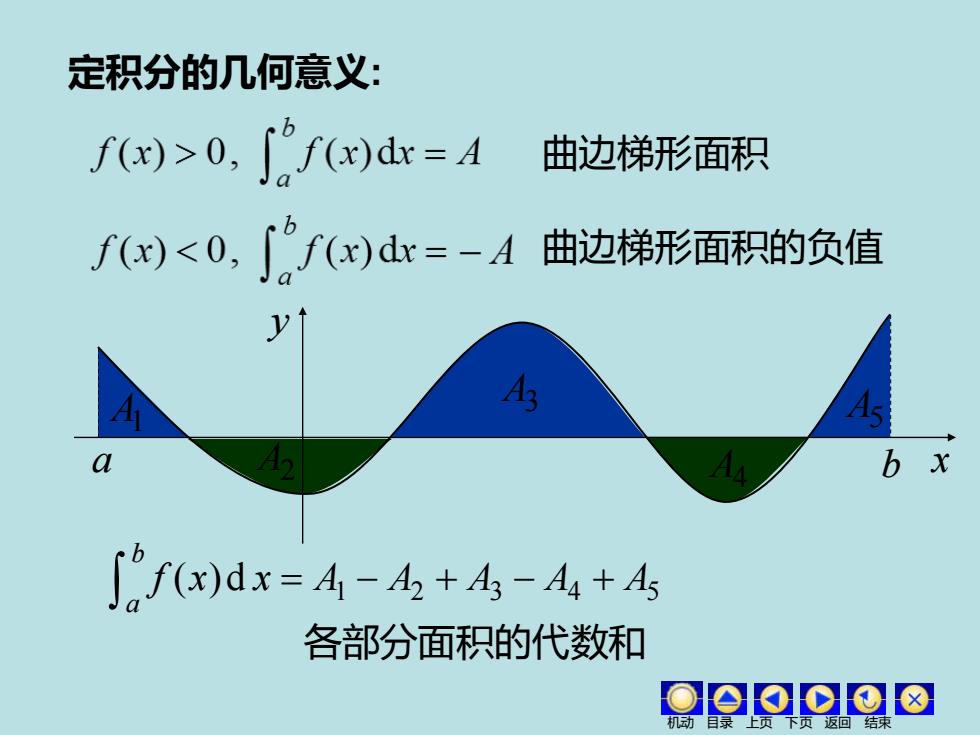
定积分的几何意义: f)>0,∫fw)dr=A 曲边梯形面积 f()<0,∫f()d=-A曲边梯形面积的负值 b ∫0fx)dx=4-4+4,-4+4 各部分面积的代数和 oeooo
定积分的几何意义: 曲边梯形面积 曲边梯形面积的负值 a b y x A1 A2 A3 A4 A5 1 2 3 4 5 f (x)d x A A A A A b a = − + − + 各部分面积的代数和 机动 目录 上页 下页 返回 结束