
第五节 第二章 西数的微分 一、微分的概念 二、微分运算法则 三、微分在近似计算中的应用 四、微分在估计误差中的应用 oooo08
二、微分运算法则 三、微分在近似计算中的应用 四、微分在估计误差中的应用 第五节 一、微分的概念 机动 目录 上页 下页 返回 结束 函数的微分 第二章

一、微分的概念 引例:一块正方形金属薄片受温度变化的影响,其 边长由xo变到x,+△x,问此薄片面积改变了多少? 设薄片边长为x,面积为A,则A=x2,当x在x取 得增量△x时,面积的增量为 △M=(+△x)2-x2 △x x0△x = 2roAr+(△)2 关于△x的 △x→0时为 xo A=x好 线性主部 高阶无穷小 故 △A≈2x0△x 称为函数在xo的微分 Q9oP0⑧
一、微分的概念 引例: 一块正方形金属薄片受温度变化的影响, 问此薄片面积改变了多少? 设薄片边长为 x , 面积为 A , 则 , 2 A = x 0 x x 面积的增量为 x x 0 2 0 A = x x x 0 2 (x) 关于△x 的 线性主部 高阶无穷小 x →0 时为 故 称为函数在 x0 的微分 当 x 在 0 x 取 得增量 x 时, 0 x 变到 , 0 边长由 x + x 其 机动 目录 上页 下页 返回 结束

定义:若函数y=f(x)在点xo的增量可表示为 △y=f(xo+△x)-f(x)=A△x+o(△x) (A为不依赖于△x的常数) 则称函数y=f(x)在点x可微,而A△x称为f(x)在 点xo的微分,记作dy或df,即 dy=A△x 定理:函数y=f(x)在点x,可微的充要条件是 y=f(x)在点xo处可导,且A=f'(xo),即 dy=f'(xo)△x Ooo⊙o8
的微分, 定义: 若函数 在点 x0 的增量可表示为 ( A 为不依赖于△x 的常数) 则称函数 y = f (x) 而 Ax 称为 记作 即 dy = Ax 定理: 函数 在点 x0 可微的充要条件是 = Ax + o(x) 即 dy = f (x )x 0 在点 可微, 机动 目录 上页 下页 返回 结束

定理:函数y=f(x)在点x,可微的充要条件是 y=f(x)在点xo处可导,且A=f'(xo),即 dy=f'(xo)△x 证:“必要性” 已知y=f(x)在点x可微,则 △y=f(x+△x)-f(x)=A△x+o(△x) 只-(4= △x→0△X△x→0 故y=f(x)在点x的可导,且f'(xo)=A
定理 : 函数 证: “必要性” 已知 在点 可微 , 则 ( ) ( ) 0 0 y = f x + x − f x ) ( ) lim lim ( 0 0 x o x A x y x x = + → → = A 故 = Ax + o(x) 在点 的可导, 且 在点 x0 可微的充要条件是 在点 处可导, 且 即 dy = f (x )x 0 机动 目录 上页 下页 返回 结束

定理:函数y=f(x)在点x,可微的充要条件是 y=f(x)在点x处可导,且A='(xo),即 dy=f'(xo)△x “充分性”已知y=f(x)在点xo的可导,则 lim △y=f'(xo) △x-→0△X Ag-fx,)+a(m=0) 故△y=f'(xo)△x+aAx=f'(xo)△x+O(△x) 线性主部 (f'(xo)≠0时) 即dy=f'(x)△x OOo⊙⊙8
定理 : 函数 在点 x0 可微的充要条件是 在点 处可导, 且 即 dy = f (x )x 0 “充分性” 已知 lim ( ) 0 0 f x x y x = → = + ( ) 0 f x x y ( lim 0 ) 0 = → x y = f (x )x +x 故 0 ( ) ( ) 0 = f x x + o x 线性主部 即 dy = f (x )x 0 在点 的可导, 则 机动 目录 上页 下页 返回 结束

说明:△y=f'(x)△x+o(△x) dy=f'(xo)△x 当f'(x0)≠0时, lim △y=lim △y Ax->0dy △x-0f'(x0)△x lim △y =1 f(o)Ax>0Ax 所以△x→0时△y与dy是等价无穷小,故当Ax 很小时,有近似公式 △y≈dy Q9o0o⑧
说明: f (x0 ) 0 时 , dy = f (x )x 0 ( ) ( ) 0 y = f x x + o x y y x d lim 0 → f x x y x = → ( ) lim 0 0 x y f x x = →0 0 lim ( ) 1 =1 所以 x → 0 时 y dy 很小时, 有近似公式 x y dy 与 是等价无穷小, 当 故当 机动 目录 上页 下页 返回 结束

微分的几何意义 切线纵坐标的增量 dy=f'(xo)△x=tana·Ax 当△x很小时,△y≈dy ↑yy=f(x) 当y=x时, Ay=是d 称△x为自变量的微分,记作dx xo x0+△x 则有 dy=f(x)dx 从而 出r 导数也叫作微商 Ooo⊙o8
微分的几何意义 dy = f (x )x 0 x + x 0 x y o y = f (x) 0 x y = tan x dy 当 x 很小时, y dy 当y = x 时, 则有 dy = f (x)dx 从而 ( ) d d f x x y = 导数也叫作微商 切线纵坐标的增量 称x为 自变量的微分, 记作 dx y = x = dx 记 机动 目录 上页 下页 返回 结束

例如,y=x3, dy x=2 =3x2.dx x=2 =0.24 dx=0.02 dx=0.02 又如,y=arctanx, dy= 2 dr 1+x 基本初等函数的微分公式(见P115表) Q99o8
例如, , 3 y = x dy d 0.02 2 = = x x 2 = 3x dx d 0.02 2 = = x x = 0.24 y = arctan x , dy x x d 1 1 2 + = 基本初等函数的微分公式 (见 P115表) 又如, 机动 目录 上页 下页 返回 结束

二、微分运算法则 设(x),vx)均可微,则 1.d(u±v)=du±dy 2.d(Cu)=Cdu (C为常数) 3.d(uv)vdu +udy 4.d()=d-dw v2 (v≠0) 5.复合函数的微分 y=f(u),u=p(x)分别可微 则复合函数y=[p(x)]的微分为 dy y dx f'(u)o'(x)dxdu dy f'(u)du 微分形式不变 Ooo⊙o8
二、 微分运算法则 设 u(x) , v(x) 均可微 , 则 (C 为常数) 分别可微 , 的微分为 = f (u)(x)dx du dy = f (u)du 微分形式不变 5. 复合函数的微分 则复合函数 = du dv = vdu + udv 机动 目录 上页 下页 返回 结束
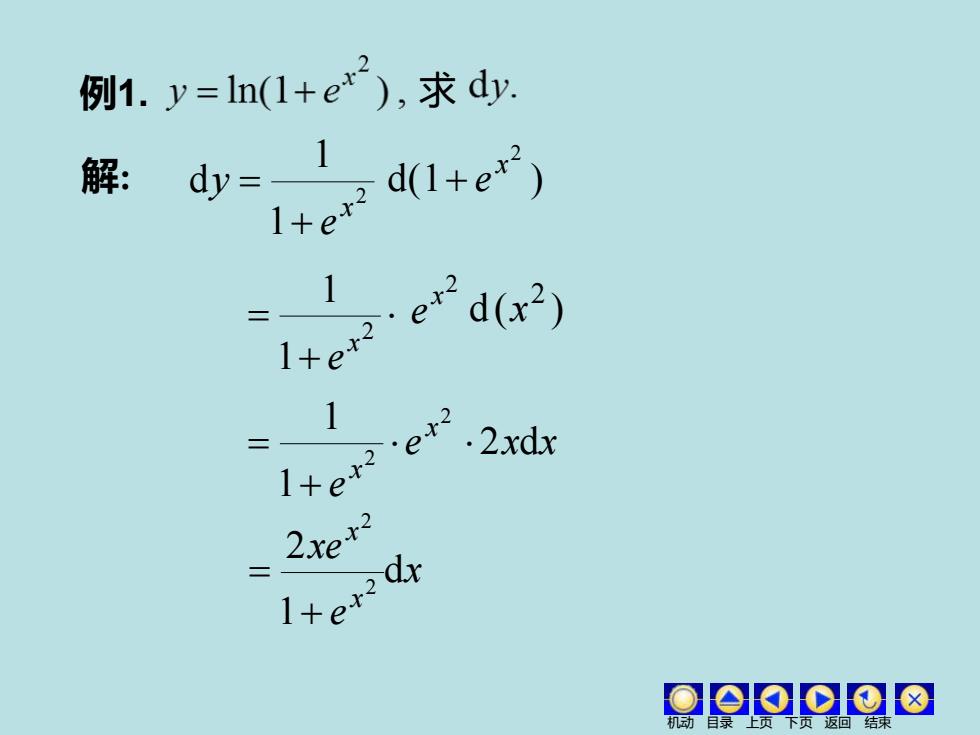
例1.y=ln(1+e),求dy i+erdl+er) 解:dy=1 1 x·2xd 2xex Oao⊙⊙8
例1. 求 解: 2 1 1 d x e y + = d(1 ) 2 x + e + = 2 1 1 x e d ( ) 2 x e x x e x x 2 d 1 1 2 2 + = x e xe x x d 1 2 2 2 + = 2 x e 机动 目录 上页 下页 返回 结束