
第三节 第六章 定积分在物理学上的友用 一、 变力沿直线所作的功 二、液体的侧压力 三、引力问题 四、转动惯量补充) Q99⊙o8
第三节 一、 变力沿直线所作的功 二、 液体的侧压力 三、 引力问题 四、 转动惯量 (补充) 机动 目录 上页 下页 返回 结束 定积分在物理学上的应用 第六章

一、变力沿直线所作的功 设物体在连续变力F(x)作用下沿x轴从x=α移动到 x=b,力的方向与运动方向平行,求变力所做的功 在[a,b]上任取子区间[x,x+dx],在其上所作的功元 素为 dW=F(x)dx a xx+dx hx 因此变力F(x)在区间[a,b]上所作的功为 w =F(x)dx OAo⊙8
一、 变力沿直线所作的功 设物体在连续变力 F(x) 作用下沿 x 轴从 x=a 移动到 力的方向与运动方向平行, 求变力所做的功 . a x x + d x b x 在其上所作的功元 素为 dW = F(x)dx 因此变力F(x) 在区间 上所作的功为 = b a W F(x)dx 机动 目录 上页 下页 返回 结束

例1.在一个带+q电荷所产生的电场作用下,一个单 位正电荷沿直线从距离点电荷a处移动到b处(a<b), 求电场力所作的功 解:当单位正电荷距离原点r时,由库仑定律电场力为 F=kg +9 +1 则功的元素为dW= ka dr 0 a rr+dr b r 所求功为 w-g月8(d 说明:电场在r=a处的电势为gdr-g
例1. 一个单 求电场力所作的功 . + q o a r r + dr b r +1 +1 解: 当单位正电荷距离原点 r 时,由库仑定律电场力为 则功的元素为 r r kq dW d 2 = 所求功为 = − r kq 1 a b ) 1 1 ( a b = kq − 说明: a k q = 机动 目录 上页 下页 返回 结束 位正电荷沿直线从距离点电荷 a 处移动到 b 处 (a < b) , 在一个带 +q 电荷所产生的电场作用下

例2.在底面积为S的圆柱形容器中盛有一定量的气 体,由于气体的膨胀,把容器中的一个面积为S的活塞从 点α处移动到点b处(如图),求移动过程中气体压力所 作的功 解:建立坐标系如图.由波义耳一马略特定律知压强 kk p与体积V成反比,即p= xs' 故作用在活塞上的 力为 F=p.S=k 功元素为 dw-Fdx=kdx o axx+dx b x X 所求功为, -f dx =k[nx]2kn Qoo⊙⊙8 机无
S 例2. 体, 求移动过程中气体压力所 o x 解: 由于气体的膨胀, 把容器中的一个面积为S 的活塞从 点 a 处移动到点 b 处 (如图), 作的功 . a b 建立坐标系如图. xx + dx 由波义耳—马略特定律知压强 p 与体积 V 成反比 , 即 功元素为 故作用在活塞上的 所求功为 机动 目录 上页 下页 返回 结束 力为 在底面积为 S 的圆柱形容器中盛有一定量的气

例3.一蓄满水的圆柱形水桶高为5m,底圆半径为3m, 试问要把桶中的水全部吸出需作多少功? 解:建立坐标系如图.在任一小区间 [x,x+dx]上的一薄层水的重力为 g·p:π32dx(KN) 5m 这薄层水吸出桶外所作的功(功元素)为 x+dx dW=9πgpxdx 3m 故所求功为 2/ X w=j9πEpxdx=-9ngP 设水的密 0 度为p =112.5πgp(KJ)
例3. 试问要把桶中的水全部吸出需作多少功 ? 解: 建立坐标系如图. o x 3m x x + d x 5m 在任一小区间 [x, x + dx] 上的一薄层水的重力为 g 3 dx 2 这薄层水吸出桶外所作的功(功元素)为 dW= 9g x dx 故所求功为 = 5 0 W 9 g x d x = 9 g 2 2 x =112.5 g ( KJ ) 设水的密 度为 机动 目录 上页 下页 返回 结束 0 5 (KN) 一蓄满水的圆柱形水桶高为 5 m, 底圆半径为3m

二、液体侧压力 设液体密度为p 深为h处的压强:p=gph ·当平板与水面平行时! h 平板一侧所受的压力为 P=PA ·当平板不与水面平行时, 面积为A的平板 所受侧压力问题就需用积分解决 QOo⊙o8
面积为 A 的平板 二、液体侧压力 设液体密度为 深为 h 处的压强: p = g h 当平板与水面平行时, h P = p A 当平板不与水面平行时, 所受侧压力问题就需用积分解决 . 机动 目录 上页 下页 返回 结束 平板一侧所受的压力为 • •
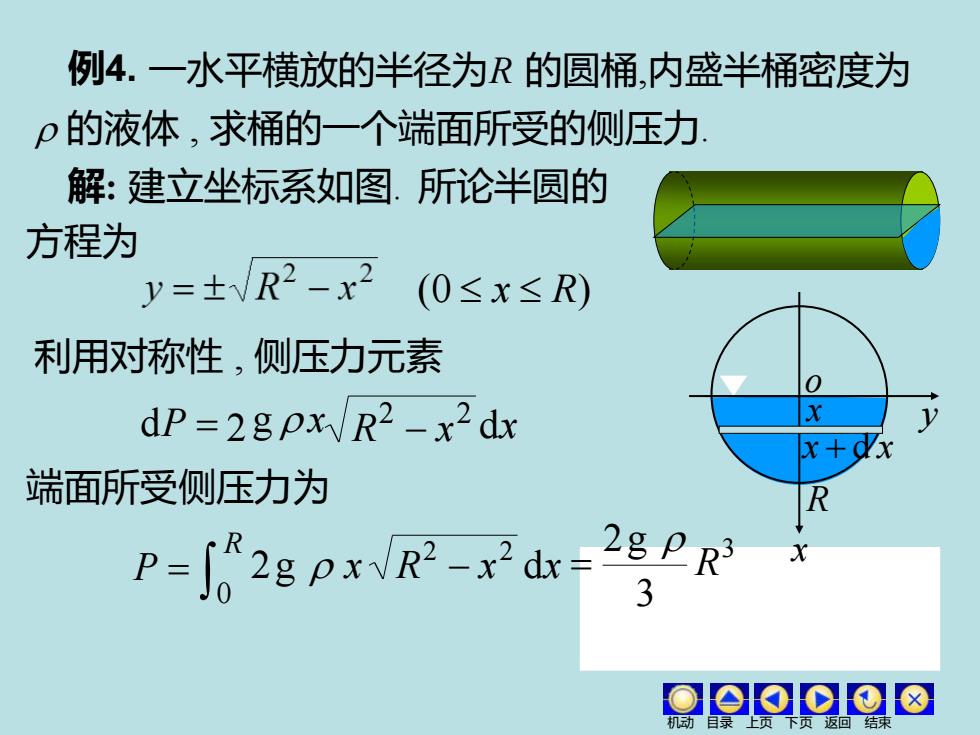
例4.一水平横放的半径为R的圆桶,内盛半桶密度为 p的液体,求桶的一个端面所受的侧压力. 解:建立坐标系如图.所论半圆的 方程为 y=±VR2-x2 (0≤x≤R) 利用对称性,侧压力元素 dP=2gpxvR2-x2dx x+dx 端面所受侧压力为 R P-528pxVR-xd-28PR 3 o0o0o8
小窄条上各点的压强 p g x 3 3 2g R = 例4. 的液体 , 求桶的一个端面所受的侧压力. 解: 建立坐标系如图. 所论半圆的 (0 x R) 利用对称性 , 侧压力元素 = R P 0 2g x R x dx 2 2 − o x y R x x + d x 2 2 dP = 2 R − x g x 端面所受侧压力为 dx 机动 目录 上页 下页 返回 结束 方程为 一水平横放的半径为R 的圆桶,内盛半桶密度为

说明:当桶内充满液体时,小窄条上的压强为gp(R+x) 侧压力元素dP=2gp(R+xWR2-x2dx, 故端面所受侧压力为 P-[2g p(R+x)R2-x2dw 0 -4RgPfR2-xd 奇函数 x+dx R 令x=Rsint(P350公式67) =4ep婚R+号6 =πgpR3 o0o08
0 arcsin 2 2 4 g 2 2 2 R R R x R x x = R − + 2 d , 2 2 R − x x 说明: 当桶内充满液体时, 小窄条上的压强为 g (R + x), 侧压力元素 dP = 故端面所受侧压力为 奇函数 3 = g R g (R + x) = − R R R x x 0 2 2 4 g d 令 x = Rsint ( P350 公式67 ) 机动 目录 上页 下页 返回 结束 o x y R x x + d x

三、引力问题 质量分别为m1,2的质点,相距r, m2 二者间的引力: 大小:F=k"2 r2 m 方向: 沿两质点的连线 若考虑物体对质点的引力,则需用积分解决 Soolo⑧
三、 引力问题 质量分别为 的质点 , 相距 r , m1 m2 r 二者间的引力 : 大小: 方向: 沿两质点的连线 若考虑物体对质点的引力, 则需用积分解决 . 机动 目录 上页 下页 返回 结束

例5.设有一长度为,线密度为μ的均匀细直棒,在 其中垂线上距α单位处有一质量为m的质点M,试计算 该棒对质点的引力 解:建立坐标系如图.细棒上小段 a [x,x+dx]对质点的引力大小为 Fy a dF=k mudx a2+x2 故垂直分力元素为 dFy=-dF cosa 2 =-k mudx dx =-kmua a2+x2 va2+x2 (a2+x2)3 QOo⊙o8 机元
例5. 设有一长度为 l, 线密度为 的均匀细直棒, 其中垂线上距 a 单位处有一质量为 m 的质点 M, M 该棒对质点的引力. 解: 建立坐标系如图. y 2 l 2 l − [x, x + dx] 细棒上小段 对质点的引力大小为 d F = k m dx 2 2 a + x 故垂直分力元素为 d Fy = −dF cos a + = − 2 2 d a x m x k 2 2 a x a + 2 3 ( ) d 2 2 a x x km a + = − a o x x 机动 目录 上页 下页 返回 结束 在 试计算 d F d Fx d Fy x + d x