
第二为 第三章 洛必达法则 一、 0型未定式 二、∞! 型未定式 00 三、其他未定式 OaO⊙o8
三、其他未定式 二、 型未定式 一、 型未定式 0 0 第二节 机动 目录 上页 下页 返回 结束 洛必达法则 第三章
函数的性态 微分中值定理 1 导数的性态 本节研究: 0 函数之商的极限1im 或”型 g(x) 转化 洛必达法则 导数之商的极限1im f'(x) g'(x) 将达.,4d Qao⊙o&
微分中值定理 函数的性态 导数的性态 函数之商的极限 导数之商的极限 转化 ( 或 型) 本节研究: 洛必达法则 洛必达 目录 上页 下页 返回 结束

型未定式 0 定理1. 1)lim f(x)=lim F(x)=0 x->a x->a 2)f(x)与F(x)在U(a)内可导,且F'(x)≠0 3 lim(x) xa F(x) 存在(或为0) lim f(x) lim f xa F(x) xaF'(x) (洛必达法则) Ooo⊙o8
一、 ( ) ( ) 3) lim F x f x x a → 存在 (或为 ) ( ) ( ) lim ( ) ( ) lim F x f x F x f x x a x a = → → 2) f (x)与F(x) 在 (a)内可导, 定理 1. 型未定式 0 0 (洛必达法则) 机动 目录 上页 下页 返回 结束

定理条件:1)limf(x)=limF(x)=0 x→a x→a 2)f(x)与F(x)在U(a)内可导,且F'(x)≠0 3)lim I(x) x-→aF'(x) 存在(或为0)》 证:无妨假设f(a)=F(@)=0,在指出的邻域内任取 x≠a,则f(x),F(x)在以x,a为端点的区间上满足柯 西定理条件,故 f(x)=f)-f(a-f'(5) (5在x,a之间) F(x)F(x)-F(a) F'(5) 1imf-limf' 13) xaF(x) x→aF'(5) xaF'(x) Oooo⊙o8 机
( 在 x , a 之间) 证: 无妨假设 f (a) = F(a) = 0, 在指出的邻域内任取 则 在以 x, a 为端点的区间上满足柯 故 ( ) ( ) ( ) ( ) ( ) ( ) F x F a f x f a F x f x − − = ( ) ( ) F f = ( ) ( ) lim F f x a = → 3) 定理条件: 西定理条件, 机动 目录 上页 下页 返回 结束 ( ) ( ) 3) lim F x f x x a → 存在 (或为 ) 2) f (x)与F(x) 在 (a)内可导,

洛必达法则 lim f(x) li (x) x→aF(x) xaF'(x) 推论1.定理1中x→a换为 x→a,x→a,x→0,X→+0,x→-00 之一,条件2)作相应的修改,定理1仍然成立 推论2.若1imN仍属0型,且f(e,F'()满足定 F'(x) 理1条件,则 lim=lim=lim f"(x) F(x) F'(x) F"(x)
推论1. 定理 1 中 x →a 换为 , → − x a 之一, 推论 2. 若 ( ) ( ) lim F x f x 理1条件, 则 条件 2) 作相应的修改 , 定理 1 仍然成立. x → +, 洛必达法则 定理1 目录 上页 下页 返回 结束

x3-3x+2 0 例1.求im 型 13-x2-x+1 0 解: 原式=lim 3x2-3 x-→1 3x2-2x-1 6x 3 lim x16x-22 注意:不是未定式不能用洛必达法则! 6x lim x-16x-2 ≠1m6=1 x→16 0008 机动
例1. 求 解: 原式 lim →1 = x 型 0 0 6 2 6 lim 1 − = → x x x 2 3 = 注意: 不是未定式不能用洛必达法则 ! 6 2 6 lim →1 x − x x 1 6 6 lim 1 = x→ 3 3 2 x − 3 2 1 2 x − x − 机动 目录 上页 下页 返回 结束
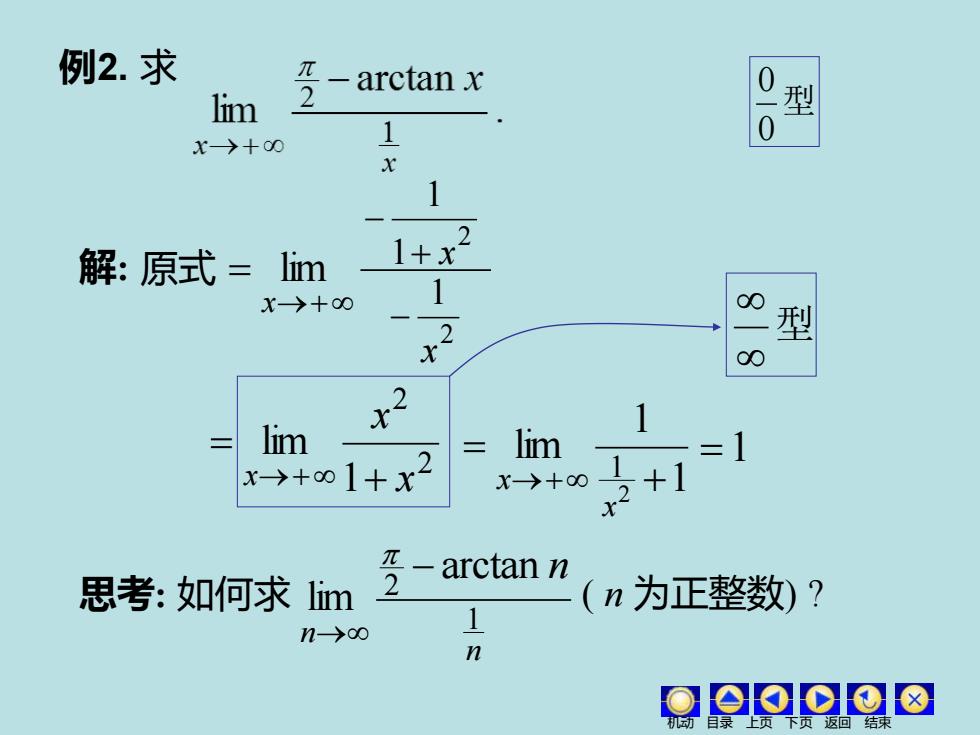
例2.求 z-arctan x lim 型 x→+00 1 0 解:原式= lim 1+x1 X→+00 1 0 型 x 0 lim x-+01+x2 lim =1 思考:如何求lim -arctan n (n为正整数)? n→0 1
例2. 求 解: 原式 lim →+ = x 型 0 0 2 2 1 lim x x x + = →+ =1 2 1 1 + x − 2 1 x − 1 1 lim 2 1 + = →+ x x 思考: 如何求 n n n 1 2 arctan lim − → ( n 为正整数) ? 型 机动 目录 上页 下页 返回 结束

00 二、 型未定式 00 定理2. 1)lim f(x)=lim F(x)=o x->a x->a 2)f(x)与F(x)在U(a)内可导,且F'(x)≠0 3)1im/'o 存在(或为o) x-→aF'(x) lim f(x) )lim f() (洛必达法则) xa F(x) )x-→aF'(x) 证:仅就极限1imfx) 存在的情形加以证明 x-→aF(x) OOoo⊙8
二、 型未定式 ( ) ( ) 3) lim F x f x x a → 存在 (或为∞) ( ) ( ) lim F x f x x→a 定理 2. 证: ( ) ( ) lim F x f x x→a 仅就极限 存在的情形加以证明 . ( ) ( ) lim F x f x x a = → (洛必达法则) 机动 目录 上页 下页 返回 结束 2) f (x)与F(x) 在 (a)内可导,
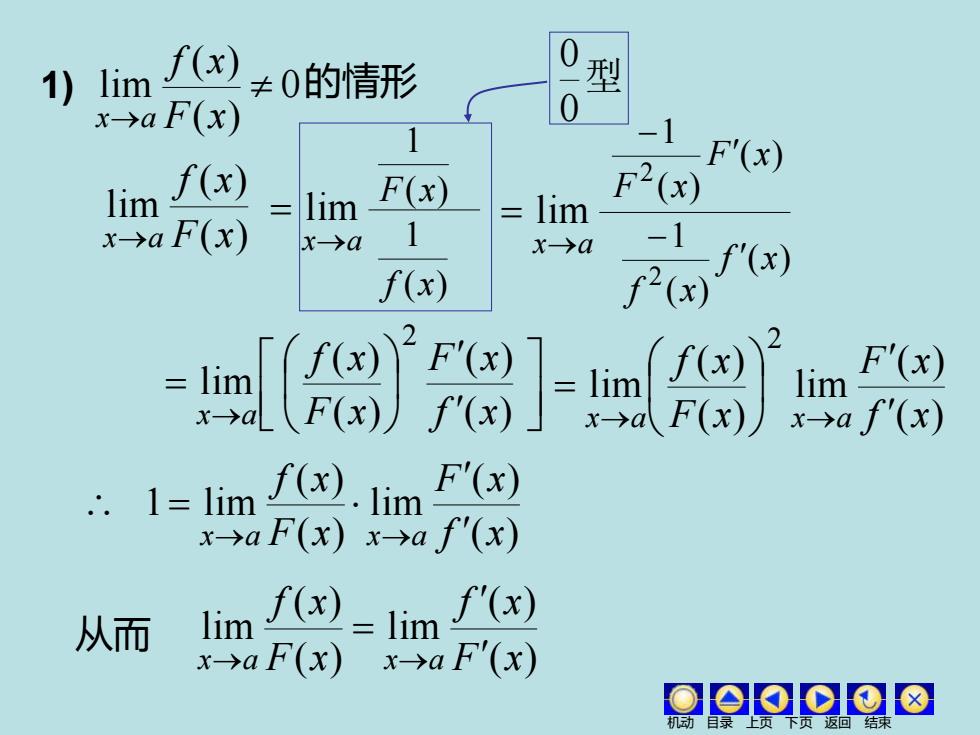
1)li f()≠0的情形 型 x→aF(x) 0 -1 lim f(x) lim F(x) F2(x) F'(x) xa F(x) lim x→a 1 x→a -1 f'(x) f(x) f2(x) 8- lim F'(x) xa f'(x) 1=limf.1im F'(x) xaF(x)xa f(x) 从而 lim f() limf(x) x→aF(x) xa F(x) Ooo⊙o8
1) 0 ( ) ( ) lim → F x f x x a 的情形 ( ) ( ) lim F x f x x→a lim x→a = ( ) 1 F x ( ) 1 f x lim x→a = ( ) ( ) 1 2 F x F x − ( ) ( ) 1 2 f x f x − = → ( ) ( ) ( ) ( ) lim 2 f x F x F x f x x a ( ) ( ) lim ( ) ( ) lim 2 f x F x F x f x x a x a = → → ( ) ( ) lim ( ) ( ) 1 lim f x F x F x f x x a x a = → → ( ) ( ) lim ( ) ( ) lim F x f x F x f x x a x a = → → 从而 型 0 0 机动 目录 上页 下页 返回 结束

2) lim f() 0的情形.取常数k≠0, x-→aF(x) 得- x→☑ F(x) lim f(x)+kF(x) F(x) =k≠0,可用1)中结论 x→a lim J(x)+kF(x) lim x-→a F'(x) f(x) lim =lim f(x) x-→aF(x)x-aF'(x) Oo⊙@8
2) 0 ( ) ( ) lim = → F x f x x a 的情形. 取常数 k 0 , = k 0, + → k F x f x x a ( ) ( ) lim ( ) ( ) ( ) lim F x f x kF x x a + = → ( ) ( ) ( ) lim F x f x kF x x a + → ( ) ( ) ( ) lim F x f x kF x x a + = → + = → k F x f x x a ( ) ( ) lim ( ) ( ) lim ( ) ( ) lim F x f x F x f x x a x a = → → 可用 1) 中结论 机动 目录 上页 下页 返回 结束