
习数课 第五章 定积分及其相关问题 一、与定积分概念有关的问题的解法 二、有关定积分计算和证明的方法 o03o08
习题课 一、与定积分概念有关的问题的解法 机动 目录 上页 下页 返回 结束 二、有关定积分计算和证明的方法 定积分及其相关问题 第五章

与定积分概念有关的问题的解法 1.用定积分概念与性质求极限 2.用定积分性质估值 3.与变限积分有关的问题 dx 解:因为x∈0,1时,0st“e 1+esx”,所以 n+1 利两夹维啊血= O9o⊙o☒
一、与定积分概念有关的问题的解法 1. 用定积分概念与性质求极限 2. 用定积分性质估值 3. 与变限积分有关的问题 机动 目录 上页 下页 返回 结束 例1. 求 d . 1 lim 1 0 x e x e x n x n → + 解: 因为 时, x n x e x e + 1 0 所以 x e x e x n x d 1 1 0 + 0 x x n d 1 0 1 1 + = n 利用夹逼准则得 d 0 1 lim 1 0 = + → x e x e x n x n , n x

说明: 1)思考例1下列做法对吗? 利用积分中值定理 原式-limeY 不对!因为5依赖于n,且0≤5≤1. 2)此类问题放大或缩小时一般应保留含参数的项 如,P265题4 1-xP≤ 1+rP1 ”分 1+x (0≤x≤1) OOo⊙⊙8
因为 依赖于 且 1) 思考例1下列做法对吗 ? 利用积分中值定理 原式 不对 ! n, 0 1. 机动 目录 上页 下页 返回 结束 说明: 2) 此类问题放大或缩小时一般应保留含参数的项 . p 1+ x 1 p p x x + = − 1 − 1 1 (0 x 1) p 1 x 如, P265 题4
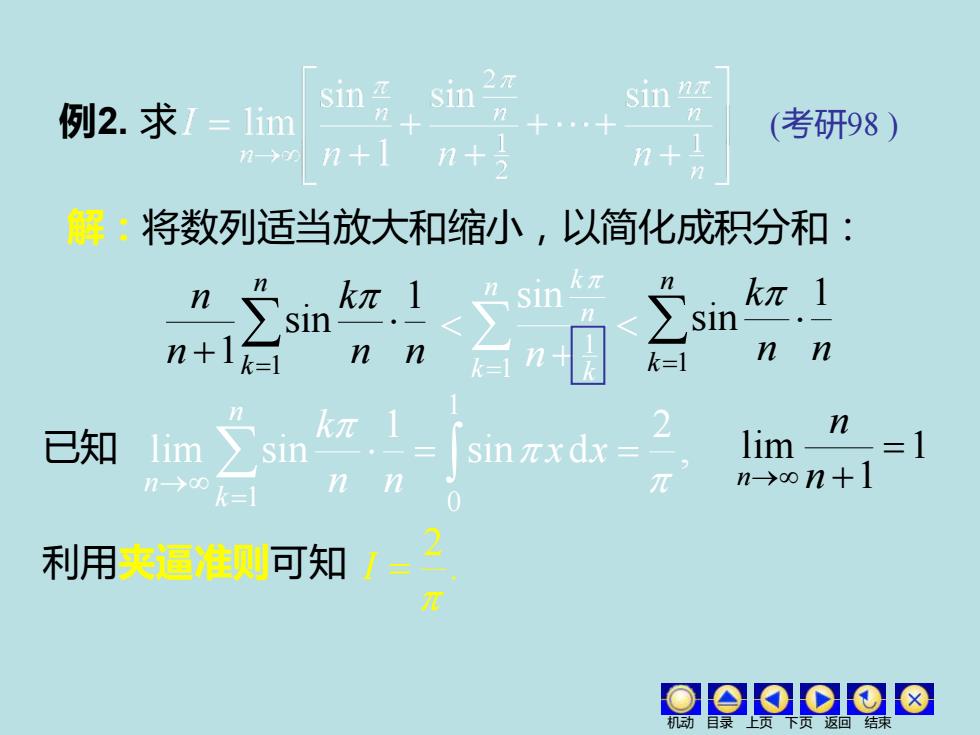
sin z 2 sin Sin 例2.求I=1im 十 (考研98) 2> n+ n+1 解:将数列适当放大和缩小,以简化成积分和: n n k元1 sin kπ1 sin n+1k1 nn 台n k=1 nn 已知 ∑sin 2 lim sin元xdx= lim =1 17→00 nn 元 n-→on+1 k三 利用夹逼准则可知 Qao⊙@8
解:将数列适当放大和缩小,以简化成积分和: + = n k k n k n 1 1 sin 已知 , 2 sin d 1 lim sin 1 1 0 = = = → x x n n k n k n 利用夹逼准则可知 . 2 I = = + n k n n k n n 1 1 sin 1 = n k n n k 1 1 sin (考研98 ) 1 1 lim = → n + n n 例2. 求 机动 目录 上页 下页 返回 结束

思考:J=1im Sin 2r Sin nz sin (n+1) + n n+ + n+. n+1 提示:由上题 Sin 2r Sin na I lim n 2 2→> n+1 n+1 元 故J=I-lim sin a Sin (n+l)z +lim n 1->0o+1 1n->o0 n+L ntl 2 2 0+0 π π OOo⊙⊙8 机
思考: 提示:由上题 1 sin lim + = − → n J I n n 1 1 ( 1) sin + + + + n n n n 1 1 ( 1) sin lim + + → + + n n n n n 2 = 2 − 0 + 0 = 机动 目录 上页 下页 返回 结束 故

练习:1求极限m(二1公平2 n n n n2+n2 解:武-e名中64ed 1 2 2n 2.求极限1im( 十.十 non+1'n+ n n 提示:lim ∑2”≤原式≤1lim∑2 n-→onil 左边=lim n-→oon+1i In 2 Qeo⊙08 目示录
练习: 1.求极限 ). 1 2 lim ( 2 2 2 2 2 n n n n n n n n + + + + + → + 解:原式 n n 1 lim → = = + n i n i 1 2 1 ( ) 1 x x d 1 1 1 0 2 + = 4 = 2. 求极限 ). 2 2 1 2 lim ( 1 2 1 1 2 n n n n n n n n n + + + + + → + 提示: 原式 n n 1 lim → = n i n i 1 2 1 lim + = → n n n = n i n i 1 2 x x 2 d 1 0 = 1 1 lim n→ n + = n i n i 1 2 左边 = 右边 机动 目录 上页 下页 返回 结束

3.估i计下列职分信4+d. 解因为4≤4-+4-,0 业小a-a 即 OooC①8 机元h
例3. 估计下列积分值 解: 因为 4 1 , 4 1 2 − x ∴ dx 2 11 0 x x d 4 1 1 0 2 − 即 2 1 6 机动 目录 上页 下页 返回 结束

4证明。≤e-x≤2c2 证:令f()=e-x,则f'(x)=(2x-10e2- 令f'()=0,得x=2 0=1,f9- 。f(2)=e2 1 f(=4e’ max f(x)=e2 [0,2] [0,2] 故 Oao⊙⊙8
例4. 证明 证: 令 则 令 得 故 机动 目录 上页 下页 返回 结束

例5.设f(x)在0,1]上是单调递减的连续函数试证 明对于任何g∈[0,1]都有不等式 ∫/o)dx≥gj/cx)d 证明:显然q=0,q=1时结论成立.当0<q<1时, -g)dx (用积分中值定理) 1-qf(5)-·(1-q)f(52) [3,] [度,1] =1-;-5≥0 故所给不等式成立 Oooo⊙8 机
例5. 设 在 上是单调递减的连续函数,试证 q0,1 都有不等式 证明:显然 q = 0,q =1 时结论成立. (用积分中值定理) ( ) 1 q f (1 ) ( ) 2 − q f 当 0 q 1 时, 故所给不等式成立 . 机动 目录 上页 下页 返回 结束 明对于任何

例6.已知f(x)在x>0处连续,f)=3,且由方程 [fodi=xfoat+ydt 确定y是x的函数,求f(x). 解:方程两端对x求导,得 f(x)y+y=∫f0d+rf0)y +y∫f)dt+yf国 令x=1,得f)y=∫f)dt+yf四 再对y求导,得00=/0=子=ny+C 令y=1,得C=3,故f(x)=31nx+3
例6. 解: 且由方程 确定 y 是 x 的函数 , 求 方程两端对 x 求导, 得 令 x = 1, 得 再对 y 求导, 得 令 y =1, 得C = 3, 机动 目录 上页 下页 返回 结束 故