
第二节 第六章 定积分在儿何学上的立用 一、 平面图形的面积 二、平面曲线的弧长 三、 已知平行截面面积函数的 立体体积 四、旋转体的侧面积补充) Ooo⊙o8
四、 旋转体的侧面积 (补充) 三、已知平行截面面积函数的 立体体积 第二节 一、 平面图形的面积 二、 平面曲线的弧长 机动 目录 上页 下页 返回 结束 定积分在几何学上的应用 第六章

一、平面图形的面积 1.直角坐标情形 y↑y=f(x 设曲线y=f(x)(≥0)与直线 x=a,x=b(a<b)及x轴所围曲 边梯形面积为A,则 o a x dA=f(x)dx A-()dx 右下图所示图形面积为 4=[f(x)-f(x)dx
一、平面图形的面积 1. 直角坐标情形 设曲线 与直线 及 x 轴所围曲 则 dA = f (x)dx o a b x y y = f (x) x x + dx A f x x b a ( )d = 机动 目录 上页 下页 返回 结束 边梯形面积为 A , 右下图所示图形面积为 y o a b x ( ) 2 ( ) y = f x 1 y = f x A f x f x x b a ( ) ( ) d = 1 − 2 x x + d x

例1.计算两条抛物线y2=x,y=x2在第一象限所围 所围图形的面积 解:由 y=x y=x2 得交点(0,0),(1,1) A-Wx-x2)dx =【 x+dx OAoO⊙o8 广士
例1. 计算两条抛物线 在第一象限所围 所围图形的面积 . x y = x 2 o y 2 y = x x x + d x 解: 由 得交点 (0, 0) , (1,1) (1,1) 1 d A ( x x )dx 2 = − 3 1 = = 1 0 A 机动 目录 上页 下页 返回 结束

例2.计算抛物线y2=2x与直线y=x-4所围图形 的面积. 解:由 y2-2x 得交点 y=x-4 (2,-2),(8,4) 为简便计算,选取y作积分变量, 则有 A=(y+4-2)d =[2y2+4y-名y3]12=18 OaoO⊙8
x y 2x 2 = o y y = x − 4 例2. 计算抛物线 y 2x 2 = 与直线 的面积 . 解: 由 得交点 (2, − 2) , (8, 4) (8,4) d A ( y 4 y )dy 2 2 1 = + − =18 y = x − 4 所围图形 (2,− 2) 为简便计算, 选取 y 作积分变量, 则有 y y + d y − = 4 2 A 机动 目录 上页 下页 返回 结束

例3.求椭圆 xD? =1所围图形的面积 a 解:利用对称性,有dA=ydx 4ydx 利用椭圆的参数方程 x=acost y=bsint (0≤t≤2π) 应用定积分换元法得 4bsint(-asint)d =4ab5 =4ab:3号=πab 当a=b时得圆面积公式 Ooo⊙⊙8 机
a b o x y x 例3. 求椭圆 解: 利用对称性 , d A = y dx 所围图形的面积 . 有 = a A y x 0 4 d 利用椭圆的参数方程 (0 2 ) sin cos = = t y b t x a t 应用定积分换元法得 = 2 0 2 4 sin d ab t t = 4ab 2 1 2 = ab 当 a = b 时得圆面积公式 机动 目录 上页 下页 返回 结束 x + d x
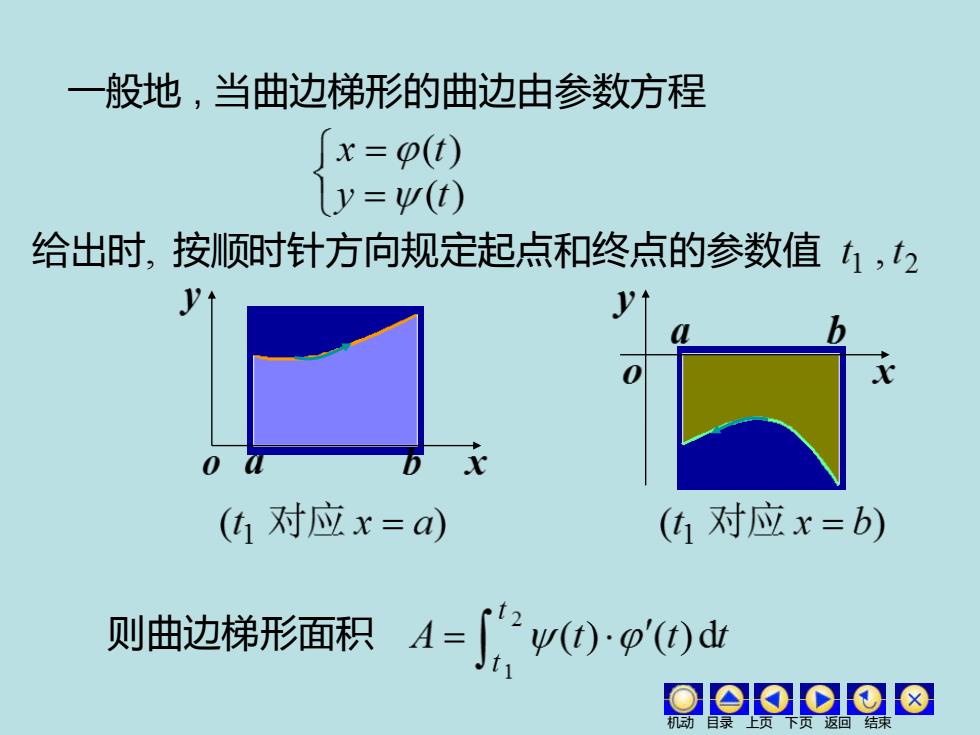
一般地,当曲边梯形的曲边由参数方程 x=p(t) (y=w(t) 给出时,按顺时针方向规定起点和终点的参数值(,2 (t对应x=a) (对应x=b) 则曲边梯形面积A=:y)p)d Oaoo⊙o8
一般地 , 当曲边梯形的曲边由参数方程 给出时, 按顺时针方向规定起点和终点的参数值 则曲边梯形面积 机动 目录 上页 下页 返回 结束

例4.求由摆线x=a(t-sint),y=a(1-cost)(a>0) 的一拱与x轴所围平面图形的面积 解:A=a1-cos0-a1-6osd! -a"(1-cost)2 dr 2πa (令u=2 =16 2.31π =3πa2 422 oooo08
例4. 求由摆线 的一拱与 x 轴所围平面图形的面积 . 解: dA = a(1− cost) a(1− cost)d t a (1 cost) d t 2 0 2 2 = − t t a d 2 4 sin 2 0 2 4 = ) 2 ( t 8a sin u d u 令u = 0 2 4 = 16a sin u d u 2 0 2 4 = 2 = 3 a = 2 0 A 机动 目录 上页 下页 返回 结束 x y o 2 a

2.极坐标情形 设p(0)∈C[a,B],p(0)≥0,求由曲线r=p(0)及 射线0=α,0=B围成的曲边扇形的面积 在区间[a,B]上任取小区间[0,0+d0] 则对应该小区间上曲边扇形面积的近似值为 dA-lo0)d0 p(0) 所求曲边扇形的面积为 4=2o2od0
2. 极坐标情形 求由曲线 及 围成的曲边扇形的面积 . r =( ) x d 在区间 上任取小区间 则对应该小区间上曲边扇形面积的近似值为 ( ) d 2 1 d 2 A = 所求曲边扇形的面积为 ( )d 2 1 2 A = 机动 目录 上页 下页 返回 结束

例5.计算阿基米德螺线r=a0(a>0)对应0从0变 到2π所围图形面积· 解4-wd 3 点击图片任意处 播放开始或暂停 Qoo⊙o8
例5. 计算阿基米德螺线 对应 从 0 变 解: x 2 a o d ( ) d 2 1 2 a = 2 0 A 2 2 a = 3 3 1 0 2 3 2 3 4 = a 点击图片任意处 播放开始或暂停 机动 目录 上页 下页 返回 结束 到 2 所围图形面积

例6.计算心形线r=a(1+cosθ)(a>0)所围图形的 面积. 解:4=202a2u+co0)Pd0 (利用对称性) ,4 2 令t=号 -8cos'dr =8a2.3.1.π3 4222 Oao⊙@8
8a cos t dt 2 0 2 4 = 例6. 计算心形线 所围图形的 面积 . 解: o 2a x d (1 cos ) d 2 1 2 2 a + = 0 2 a d 2 4cos4 (利用对称性) 2 令t = = 2 8a 4 3 2 1 2 2 2 3 = a 心形线 目录 上页 下页 返回 结束